Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah fungsi polinom berderajat dua. Fungsi $f(x)$ dengan daerah definisi $x ∈ R$ yang ditentukan oleh $f(x) = ax^{2} + bx + c$, dengan $a,\ b,\ dan\ c ∈ R$ serta $a ≠ 0$ disebut fungsi kuadrat. Sehingga, bentuk umum dari fungsi kuadrat
adalah: $f : x → ax^2 + bx + c$ atau $f(x) = ax^2 + bx + c$. Grafik fungsi kuadrat $f(x) = ax^{2} + bx + c = 0$ atau $y = ax^{2} + bx + c = 0$ disebut parabola. Parabola adalah kurva lengkung yang arah bukaannya tertentu. Topik bahasan kita kali ini adalah parabola yang terbuka keatas atau yang terbuka kebawah.
Sketsa Grafik Fungsi Kuadrat
Fungsi kuadrat dapat digambarkan atau disketsakan dengan menggunakan koordinat Cartesius. Untuk membuat sketsa fungsi kuadrat atau parabola, kita
harus mengikuti langkah-langkah sebagai berikut:
Contoh soal 1.
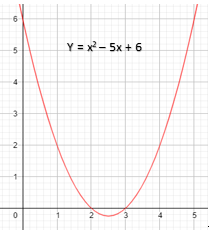
Lukislah sketsa dari fungsi kuadrat $f(x) = x^{2} - 5x + 6$
Menyusun Persamaan Fungsi Kuadrat
Kita sudah belajar menggambar sketsa grafik fungsi kuadrat. Bagaimana menyusun persamaan fungsi kuadrat jika sketsa atau grafiknya diketahui? Kita dapat menyusun persamaan fungsi kuadrat jika:
1. Tiga titik yang dilalui kurva diketahui.
Persamaan fungsi dapat dicari dengan melakukan substitusi masing-masing titik kedalam persamaan: $y = f(x) = ax^{2} + bx + c$. Kita akan mendapatkan tiga persamaan dengan tiga variabel.
2. Titik potong sumbu $x$ diketahui dan salah satu titik yang dilalui diketahui. Substitusi titik potong dengan sumbu $x$ dan titik yang dilalui kedalam persamaan: $y = a(x - x_1)(x - x_2)$, $x_1\ dan\ x_2$ adalah titik potong sumbu $x$.
3. Koordinat titik puncak (P, Q) diketahui dan salah satu titik yang dilalui diketahui. Substitusi titik puncak dan titik yang dilalui kedalam persamaan: $y = f(x) = a(x - P)^{2} + Q$.
$P\ dan\ Q$ adalah koordinat titik puncak.
Contoh soal 2.
Tentukan persamaan parabola yang melalui titik $A(1, 4),\ B(0, 5),\ dan\ C(-1, 8)$.
Contoh soal 3.
Tentukan persamaan parabola yang memotong sumbu $x$ di titik $(2, 0)\ dan\ (3, 0)$ serta melalui titik $(0, 6)$.
Contoh soal 4.
Tentukan persamaan parabola yang puncaknya $(1, 3)$ dan melalui titik $(2, 5)$.
Supaya adik-adik lebih paham tentang fungsi kuadrat, pelajari soal dan pembahasan fungsi kuadrat berikut.
Demikianlah Soal dan Pembahasan Fungsi Kuadrat. Selamat belajar !
SHARE THIS POST www.maretong.com
Fungsi kuadrat adalah fungsi polinom berderajat dua. Fungsi $f(x)$ dengan daerah definisi $x ∈ R$ yang ditentukan oleh $f(x) = ax^{2} + bx + c$, dengan $a,\ b,\ dan\ c ∈ R$ serta $a ≠ 0$ disebut fungsi kuadrat. Sehingga, bentuk umum dari fungsi kuadrat
adalah: $f : x → ax^2 + bx + c$ atau $f(x) = ax^2 + bx + c$. Grafik fungsi kuadrat $f(x) = ax^{2} + bx + c = 0$ atau $y = ax^{2} + bx + c = 0$ disebut parabola. Parabola adalah kurva lengkung yang arah bukaannya tertentu. Topik bahasan kita kali ini adalah parabola yang terbuka keatas atau yang terbuka kebawah.
Sketsa Grafik Fungsi Kuadrat
Fungsi kuadrat dapat digambarkan atau disketsakan dengan menggunakan koordinat Cartesius. Untuk membuat sketsa fungsi kuadrat atau parabola, kita
harus mengikuti langkah-langkah sebagai berikut:
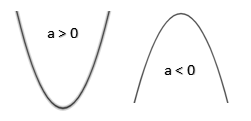
1. Menentukan arah bukaan kurva.
Kurva yang kita bahas disini adalah kurva yang terbuka ke atas atau kebawah.
A. Grafik terbuka keatas jika $a > 0$
B. Grafik terbuka kebawah jika $a < 0$
2. Menentukan titik potong terhadap sumbu $x$.
Titik potong terhadap sumbu $x → y = 0$
$ax^{2} + bx + c = 0$
$(i).\ D > 0$ → kurva memotong sumbu $x$ di dua titik yang berbeda
$(ii).\ D = 0$ → kurva menyinggung sumbu $x$
$(iii).\ D < 0$ → kurva menjauhi sumbu $x$
3. Menentukan titik potong terhadap sumbu y.
Titik potong terhadap sumbu $y → x = 0$.
$y = a.0^2 + b.0 + c$,
$y = c$
Berarti kurva memotong sumbu $y$ di titik $(0, c)$
4. menentukan sumbu simetri.
Persamaan sumbu simetri: $x = -\dfrac{b}{2a}$
5. Menentukan titik puncak parabola.
$Titik\ puncak = \left\{-\dfrac{b}{2a}, \dfrac{b^{2} - 4ac}{-4a}\right\}$
$Titik\ puncak = \left\{-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right\}$
Note:
Titik puncak sering juga disebut sebagai titik maksimum atau titik minimum atau titik balik. Jika $a > 0$, kurva akan terbuka ke atas sehingga yang ada adalah titik minimum. Jika $a < 0$, kurva akan terbuka ke bawah sehingga yang ada adalah titik maksimum.
Kurva yang kita bahas disini adalah kurva yang terbuka ke atas atau kebawah.
A. Grafik terbuka keatas jika $a > 0$
B. Grafik terbuka kebawah jika $a < 0$
2. Menentukan titik potong terhadap sumbu $x$.
Titik potong terhadap sumbu $x → y = 0$
$ax^{2} + bx + c = 0$
$(i).\ D > 0$ → kurva memotong sumbu $x$ di dua titik yang berbeda
$(ii).\ D = 0$ → kurva menyinggung sumbu $x$
$(iii).\ D < 0$ → kurva menjauhi sumbu $x$
3. Menentukan titik potong terhadap sumbu y.
Titik potong terhadap sumbu $y → x = 0$.
$y = a.0^2 + b.0 + c$,
$y = c$
Berarti kurva memotong sumbu $y$ di titik $(0, c)$
4. menentukan sumbu simetri.
Persamaan sumbu simetri: $x = -\dfrac{b}{2a}$
5. Menentukan titik puncak parabola.
$Titik\ puncak = \left\{-\dfrac{b}{2a}, \dfrac{b^{2} - 4ac}{-4a}\right\}$
$Titik\ puncak = \left\{-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right\}$
Note:
Titik puncak sering juga disebut sebagai titik maksimum atau titik minimum atau titik balik. Jika $a > 0$, kurva akan terbuka ke atas sehingga yang ada adalah titik minimum. Jika $a < 0$, kurva akan terbuka ke bawah sehingga yang ada adalah titik maksimum.
Contoh soal 1.
Lukislah sketsa dari fungsi kuadrat $f(x) = x^{2} - 5x + 6$
$(i).\ a = 1 > 0$ → kurva atau grafik terbuka keatas.
$(ii).$ Titik potong terhadap sumbu $x → y = 0$.
$x^{2} - 5x + 6 = 0$
$(x - 2)((x - 3) = 0$
$x = 2\ atau\ x = 3$
titik potong sumbu $x$ adalah $(2, 0)\ dan\ (3, 0)$
$(iii).$ Titik potong terhadap sumbu $y → x = 0$.
$y = 0^{2} - 5.0 + 6.$
$y = 6$
Sehingga titik potong sumbu $y = (0, 6)$
$(iv)$. Sumbu simetri:
$x = -\dfrac{b}{2a}$
$x = -\dfrac{-5}{2}$
$x = \dfrac{5}{2}$
$(v).\ Titik\ puncak = \left\{-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right\}$
$= \left(\dfrac{5}{2}, f(\dfrac{5}{2})\right)$
$= \left(\dfrac{5}{2}, -\dfrac{1}{4}\right)$
Sketsa
$(ii).$ Titik potong terhadap sumbu $x → y = 0$.
$x^{2} - 5x + 6 = 0$
$(x - 2)((x - 3) = 0$
$x = 2\ atau\ x = 3$
titik potong sumbu $x$ adalah $(2, 0)\ dan\ (3, 0)$
$(iii).$ Titik potong terhadap sumbu $y → x = 0$.
$y = 0^{2} - 5.0 + 6.$
$y = 6$
Sehingga titik potong sumbu $y = (0, 6)$
$(iv)$. Sumbu simetri:
$x = -\dfrac{b}{2a}$
$x = -\dfrac{-5}{2}$
$x = \dfrac{5}{2}$
$(v).\ Titik\ puncak = \left\{-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right\}$
$= \left(\dfrac{5}{2}, f(\dfrac{5}{2})\right)$
$= \left(\dfrac{5}{2}, -\dfrac{1}{4}\right)$
Sketsa
Menyusun Persamaan Fungsi Kuadrat
Kita sudah belajar menggambar sketsa grafik fungsi kuadrat. Bagaimana menyusun persamaan fungsi kuadrat jika sketsa atau grafiknya diketahui? Kita dapat menyusun persamaan fungsi kuadrat jika:
1. Tiga titik yang dilalui kurva diketahui.
Persamaan fungsi dapat dicari dengan melakukan substitusi masing-masing titik kedalam persamaan: $y = f(x) = ax^{2} + bx + c$. Kita akan mendapatkan tiga persamaan dengan tiga variabel.
2. Titik potong sumbu $x$ diketahui dan salah satu titik yang dilalui diketahui. Substitusi titik potong dengan sumbu $x$ dan titik yang dilalui kedalam persamaan: $y = a(x - x_1)(x - x_2)$, $x_1\ dan\ x_2$ adalah titik potong sumbu $x$.
3. Koordinat titik puncak (P, Q) diketahui dan salah satu titik yang dilalui diketahui. Substitusi titik puncak dan titik yang dilalui kedalam persamaan: $y = f(x) = a(x - P)^{2} + Q$.
$P\ dan\ Q$ adalah koordinat titik puncak.
Contoh soal 2.
Tentukan persamaan parabola yang melalui titik $A(1, 4),\ B(0, 5),\ dan\ C(-1, 8)$.
substitusi atau masukkan ketiga titik kedalam persamaan: $y = ax^{2} + bx + c$
$(1, 4) → 4 = a + b + c$ .... *
$(0, 5) → 5 = c → c = 5$ .... **
$(-1, 8) → 8 = a - b + c$ .... ***
eliminasi persamaan * dan **
$a + b + c = 4$
$a - b + c = 8$
------------------------ $-$
$2a + 2c = 12$ → semua dibagi 2.
$a + c = 6$
dengan memasukkan nilai $c = 5$,
$a + 5 = 6 → a = 1$.
substitusi $a = 1\ dan\ c = 5$ kedalam persamaan *
$a + b + c = 4$
$1 + b + 5 = 4$
$b = -2$.
maka persamaan fungsi kuadrat tersebut adalah:
$y = x^{2} - 2x + 5 = 0$
$(1, 4) → 4 = a + b + c$ .... *
$(0, 5) → 5 = c → c = 5$ .... **
$(-1, 8) → 8 = a - b + c$ .... ***
eliminasi persamaan * dan **
$a + b + c = 4$
$a - b + c = 8$
------------------------ $-$
$2a + 2c = 12$ → semua dibagi 2.
$a + c = 6$
dengan memasukkan nilai $c = 5$,
$a + 5 = 6 → a = 1$.
substitusi $a = 1\ dan\ c = 5$ kedalam persamaan *
$a + b + c = 4$
$1 + b + 5 = 4$
$b = -2$.
maka persamaan fungsi kuadrat tersebut adalah:
$y = x^{2} - 2x + 5 = 0$
Contoh soal 3.
Tentukan persamaan parabola yang memotong sumbu $x$ di titik $(2, 0)\ dan\ (3, 0)$ serta melalui titik $(0, 6)$.
$x_1 = 2\ dan\ x_2 = 3$
$y = a(x - x_1)(x - x_2)$
$y = a(x - 2)(x - 3)$ .... *
Masukkan titik $(0, 6)$ ke dalam pers *
$6 = a(0 - 2)(0 - 3)$ ← titik yang dilalui.
$6 = 6a → a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1(x - 2)(x - 3)$
$y = x^{2} - 5x + 6$
$y = a(x - x_1)(x - x_2)$
$y = a(x - 2)(x - 3)$ .... *
Masukkan titik $(0, 6)$ ke dalam pers *
$6 = a(0 - 2)(0 - 3)$ ← titik yang dilalui.
$6 = 6a → a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1(x - 2)(x - 3)$
$y = x^{2} - 5x + 6$
Contoh soal 4.
Tentukan persamaan parabola yang puncaknya $(1, 3)$ dan melalui titik $(2, 5)$.
$P = 1\ dan\ Q = 3$
$y = a(x - P)^{2} + Q$
$y = a(x - 1)^{2} + 3$ ← titik puncak .... *
$5 = a(2 - 1)^{2} + 3$ ← titk yang dilalui.
$5 = a + 3$
$2 = a$
masukkan $a = 2$ kedalam persamaan *
$y = 2(x - 1)^{2} + 3$
$y = 2(x^{2} - 2x + 1) + 3$
$y = 2x^{2} - 4x + 2 + 3$
$y = 2x^{2} - 4x + 5$
$y = a(x - P)^{2} + Q$
$y = a(x - 1)^{2} + 3$ ← titik puncak .... *
$5 = a(2 - 1)^{2} + 3$ ← titk yang dilalui.
$5 = a + 3$
$2 = a$
masukkan $a = 2$ kedalam persamaan *
$y = 2(x - 1)^{2} + 3$
$y = 2(x^{2} - 2x + 1) + 3$
$y = 2x^{2} - 4x + 2 + 3$
$y = 2x^{2} - 4x + 5$
Supaya adik-adik lebih paham tentang fungsi kuadrat, pelajari soal dan pembahasan fungsi kuadrat berikut.
Soal dan Pembahasan Fungsi Kuadrat
$1.$ Fungsi kuadrat $y = x^{2} - 4x - 5$ mempunyai titik . . . .
$A.\ minimum\ (2, -9)$
$B.\ maksimum\ (-2, 9)$
$C.\ minimum\ (-2, -7)$
$D.\ maksimum\ (-2, 7)$
$E.\ minimum\ (2, 9)$
[Fungsi Kuadrat]
$A.\ minimum\ (2, -9)$
$B.\ maksimum\ (-2, 9)$
$C.\ minimum\ (-2, -7)$
$D.\ maksimum\ (-2, 7)$
$E.\ minimum\ (2, 9)$
[Fungsi Kuadrat]
$y = x^{2} - 4x - 5$
$a = 1 > 0$, berarti kurva terbuka ke atas. jika kurva terbuka keatas, yang ada adalah nilai minimum.
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-4)}{2.1}$
$x = 2$
Nilai maks/min $= f\left(\dfrac{-b}{2a}\right)$
$= f(2)$
$= 2^{2} - 4.2 - 5$
$= -9$
Jadi titik minimum $= (2, -9)$ → A.
$a = 1 > 0$, berarti kurva terbuka ke atas. jika kurva terbuka keatas, yang ada adalah nilai minimum.
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-4)}{2.1}$
$x = 2$
Nilai maks/min $= f\left(\dfrac{-b}{2a}\right)$
$= f(2)$
$= 2^{2} - 4.2 - 5$
$= -9$
Jadi titik minimum $= (2, -9)$ → A.
$2.$ Jika fungsi kuadrat $y = mx^{2} - 6x + m - 1$ mempunyai $nilai\ minimum\ = 7$, maka nilai $m =$ . . . .
$A.\ 9$
$B.\ 1$
$C.\ -9\ atau\ -1$
$D.\ -1\ atau\ 9$
$E.\ -9\ atau\ 1$
[Fungsi Kuadrat]
$A.\ 9$
$B.\ 1$
$C.\ -9\ atau\ -1$
$D.\ -1\ atau\ 9$
$E.\ -9\ atau\ 1$
[Fungsi Kuadrat]
$y = mx^{2} - 6x + m - 1$
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-6)}{2m}$
$x = \dfrac{3}{m}$
Nilai maks/min $= f\left(\dfrac{-b}{2a}\right)$
$7 = f\left(\dfrac{3}{m}\right)$
$7 = m\left(\dfrac{3}{m}\right)^{2} - 6.\dfrac{3}{m} + m - 1$
$7 = \dfrac{9}{m} - \dfrac{18}{m} + m - 1$
$8 = \dfrac{-9}{m} + m$
$m^{2} - 8m - 9 = 0$
$(m + 1)(m - 9) = 0$
$m = -1\ atau\ m = 9$
Jika $m = -1$, kurva akan terbuka kebawah dan yang ada adalah nilai maksimum. Yang diminta adalah nilai $m$ yang membuat nilai minimum. $m\ harus\ > 0$. jadi yang memenuhi syarat adalah $m = 9$ → A.
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-6)}{2m}$
$x = \dfrac{3}{m}$
Nilai maks/min $= f\left(\dfrac{-b}{2a}\right)$
$7 = f\left(\dfrac{3}{m}\right)$
$7 = m\left(\dfrac{3}{m}\right)^{2} - 6.\dfrac{3}{m} + m - 1$
$7 = \dfrac{9}{m} - \dfrac{18}{m} + m - 1$
$8 = \dfrac{-9}{m} + m$
$m^{2} - 8m - 9 = 0$
$(m + 1)(m - 9) = 0$
$m = -1\ atau\ m = 9$
Jika $m = -1$, kurva akan terbuka kebawah dan yang ada adalah nilai maksimum. Yang diminta adalah nilai $m$ yang membuat nilai minimum. $m\ harus\ > 0$. jadi yang memenuhi syarat adalah $m = 9$ → A.
$3.$ Persamaan sumbu simetri dari parabola $y = x^{2} + 6x + 5$ adalah . . . .
$A.\ x = 3$
$B.\ x = -3$
$C.\ x = 2$
$D.\ y = 3$
$E.\ y = -3$
[Fungsi Kuadrat]
$A.\ x = 3$
$B.\ x = -3$
$C.\ x = 2$
$D.\ y = 3$
$E.\ y = -3$
[Fungsi Kuadrat]
$y = x^{2} + 6x + 5$
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-6}{2.1}$
$x = -3$ → B.
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-6}{2.1}$
$x = -3$ → B.
$4.$ Jika fungsi kuadrat $y = ax^{2} - (6 + a)x + 3$ mempunyai sumbu simetri $x = 2$, maka nilai $a$ yang memenuhi adalah . . . .
$A.\ 1$
$B.\ 2$
$C.\ 3$
$D.\ -1$
$E.\ -2$
[Fungsi Kuadrat]
$A.\ 1$
$B.\ 2$
$C.\ 3$
$D.\ -1$
$E.\ -2$
[Fungsi Kuadrat]
$y = ax^{2} - (6 + a)x + 3$
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$2 = \dfrac{-(-(6 + a))}{2.a}$
$2 = \dfrac{6 + a}{2a}$
$4a = 6 + a$
$3a = 6$
$a = 2$→ B.
Sumbu simetri:
$x = \dfrac{-b}{2a}$
$2 = \dfrac{-(-(6 + a))}{2.a}$
$2 = \dfrac{6 + a}{2a}$
$4a = 6 + a$
$3a = 6$
$a = 2$→ B.
$5.$ Parabola $y = x^{2} + mx + n$ memotong sumbu $x$ di titik $(2, 0)$ dan $(6, 0)$. Maka persamaan sumbu simetri dari parabola tersebut adalah . . . .
$A.\ x = 3$
$B.\ x = 4$
$C.\ x = -3$
$D.\ x = -4$
$E.\ x = 5$
[Fungsi Kuadrat]
$A.\ x = 3$
$B.\ x = 4$
$C.\ x = -3$
$D.\ x = -4$
$E.\ x = 5$
[Fungsi Kuadrat]
$y = x^{2} + mx + n$
Jika titik potong sumbu $x$ diketahui $(x_1, 0)\ dan\ (x_2, 0)$ maka persamaan sumbu simetri bisa dicari dengan menggunakan rumus:
$x = \dfrac{x_1 + x_2}{2}$
$x = \dfrac{2 + 6}{2}$
$x = 4$ → B.
Jika titik potong sumbu $x$ diketahui $(x_1, 0)\ dan\ (x_2, 0)$ maka persamaan sumbu simetri bisa dicari dengan menggunakan rumus:
$x = \dfrac{x_1 + x_2}{2}$
$x = \dfrac{2 + 6}{2}$
$x = 4$ → B.
$6.$ Jika parabola $y = x^{2} + x + m + 2$ memotong sumbu $y$ positif, maka nilai m yang memenuhi adalah . . . .
$A.\ m > 2$
$B.\ m < 2$
$C.\ m > -2$
$D.\ m < -2$
$E.\ -2 < m < 2$
[Fungsi Kuadrat]
$A.\ m > 2$
$B.\ m < 2$
$C.\ m > -2$
$D.\ m < -2$
$E.\ -2 < m < 2$
[Fungsi Kuadrat]
$y = x^{2} + x + m + 2$
Parabola memotong sumbu $y$ positif jika $c > 0$.
$m + 2 > 0$
$m > -2$ → C.
Parabola memotong sumbu $y$ positif jika $c > 0$.
$m + 2 > 0$
$m > -2$ → C.
$7.$ Nilai $m$ agar grafik fungsi kuadrat $y = mx^{2} + 2mx + 2 - m$ menyinggung sumbu $x$ adalah . . . .
$A.\ 0$
$B.\ 1$
$C.\ 2$
$D.\ 3$
$E.\ 0\ dan\ 1$
[Fungsi Kuadrat]
$A.\ 0$
$B.\ 1$
$C.\ 2$
$D.\ 3$
$E.\ 0\ dan\ 1$
[Fungsi Kuadrat]
$y = mx^{2} + 2mx + 2 - m$
Kurva menyinggung sumbu $x\ jika\ D = 0$.
$(2m)^{2} - 4.m.(2 - m) = 0$
$4m^{2} - 8m + 4m^{2} = 0$
$8m^{2} - 8m = 0$
$m^{2} - m = 0$
$m(m - 1) = 0$
$m = 0\ atau\ m = 1$
Jika $m = 0$, tidak akan ada fungsi kuadrat.
Jadi $m = 0$ tidak memenuhi syarat.
Sehingga $m = 1$ → B.
Kurva menyinggung sumbu $x\ jika\ D = 0$.
$(2m)^{2} - 4.m.(2 - m) = 0$
$4m^{2} - 8m + 4m^{2} = 0$
$8m^{2} - 8m = 0$
$m^{2} - m = 0$
$m(m - 1) = 0$
$m = 0\ atau\ m = 1$
Jika $m = 0$, tidak akan ada fungsi kuadrat.
Jadi $m = 0$ tidak memenuhi syarat.
Sehingga $m = 1$ → B.
$8.$ Supaya parabola $y = px^{2} + 4x + 2$ selalu berada di atas sumbu $x$, nilai $p$ yang memenuhi adalah . . . .
$A.\ 0 < p < 2$
$B.\ -2 < p < 0$
$C.\ p < 2$
$D.\ p > 2$
$E.\ p > -2$
[Fungsi Kuadrat]
$A.\ 0 < p < 2$
$B.\ -2 < p < 0$
$C.\ p < 2$
$D.\ p > 2$
$E.\ p > -2$
[Fungsi Kuadrat]
$y = px^{2} + 4x + 2$
Kurva selalu berada di atas sumbu $x$ (definit positif) jika $a > 0\ dan\ D < 0$.
$(i).\ p > 0$ .... *
$(ii).\ 4^{2} - 4.p.2 < 0$
$16 - 8p < 0$
$16 < 8p$
$8p > 16$
$p > 2$ .... **
$(*) ∩ (**) → p > 2$ → D.
Kurva selalu berada di atas sumbu $x$ (definit positif) jika $a > 0\ dan\ D < 0$.
$(i).\ p > 0$ .... *
$(ii).\ 4^{2} - 4.p.2 < 0$
$16 - 8p < 0$
$16 < 8p$
$8p > 16$
$p > 2$ .... **
$(*) ∩ (**) → p > 2$ → D.
$9.$ Persamaan parabola yang melalui titik $(1, -6),\ (2, -5)\ dan\ (-2, 15)$ adalah . . . .
$A.\ y = 2x^{2} - 5x - 3$
$B.\ y = 2x^{2} - 3x - 5$
$C.\ y = 2x^{2} + 5x - 3$
$D.\ y = 2x^{2} + 3x - 5$
$E.\ y = 2x^{2} + 5x + 3$
[Fungsi Kuadrat]
$A.\ y = 2x^{2} - 5x - 3$
$B.\ y = 2x^{2} - 3x - 5$
$C.\ y = 2x^{2} + 5x - 3$
$D.\ y = 2x^{2} + 3x - 5$
$E.\ y = 2x^{2} + 5x + 3$
[Fungsi Kuadrat]
Titik $(1, -6),\ (2, -5)\ dan\ (-2, 15)$ substitusi kedalam persamaan $y = ax^{2} + bx + c$
$substitusi\ titik\ (1, -6)$
$-6 = a.1^{2} + b.1 + c$
$-6 = a + b + c$ .... (1)
$substitusi\ titik\ (2, -5)$
$-5 = a. 2^{2} + b.2 + c$
$-5 = 4a + 2b + c$ .... (2)
$substitusi\ titik\ (-2, 15)$
$15 = a(-2)^{2} + b.(-2) + c$
$15 = 4a - 2b + c$ .... (3)
eliminasi persamaan (1) dan (2)
$-6 = a + b + c$
$-5 = 4a + 2b + c$
----------------------------- $-$
$1 = 3a + b$ .... (4)
eliminasi persamaan (2) dan (3)
$-5 = 4a + 2b + c$
$15 = 4a - 2b + c$
----------------------------- $-$
$-20 = 4b$
$b = -5$.
substitusi $b = -5$ kedalam persamaan (4)
$1 = 3a - 5$
$6 = 3a$
$a = 2$
substitusi $a = 2\ dan\ b = -5$ kedalam persamaan (1)
$-6 = 2 - 5 + c$
$c = -3$.
maka persamaan kuadrat tersebut adalah:
$y = 2x^{2} - 5x - 3$ → A.
$substitusi\ titik\ (1, -6)$
$-6 = a.1^{2} + b.1 + c$
$-6 = a + b + c$ .... (1)
$substitusi\ titik\ (2, -5)$
$-5 = a. 2^{2} + b.2 + c$
$-5 = 4a + 2b + c$ .... (2)
$substitusi\ titik\ (-2, 15)$
$15 = a(-2)^{2} + b.(-2) + c$
$15 = 4a - 2b + c$ .... (3)
eliminasi persamaan (1) dan (2)
$-6 = a + b + c$
$-5 = 4a + 2b + c$
----------------------------- $-$
$1 = 3a + b$ .... (4)
eliminasi persamaan (2) dan (3)
$-5 = 4a + 2b + c$
$15 = 4a - 2b + c$
----------------------------- $-$
$-20 = 4b$
$b = -5$.
substitusi $b = -5$ kedalam persamaan (4)
$1 = 3a - 5$
$6 = 3a$
$a = 2$
substitusi $a = 2\ dan\ b = -5$ kedalam persamaan (1)
$-6 = 2 - 5 + c$
$c = -3$.
maka persamaan kuadrat tersebut adalah:
$y = 2x^{2} - 5x - 3$ → A.
$10.$ Diketahui titik balik suatu parabola adalah $(2, 6)$ dan parabola melalui titik $(1, 5)$. Persamaan parabola adalah . . . .
$A.\ y = x^{2} + 4x + 2$
$B.\ y = -x^{2} - 4x + 2$
$C.\ y = x^{2} - 4x - 2$
$D.\ y = -x^{2} + 4x + 2$
$E.\ y = -x^{2} - 4x - 2$
[Fungsi Kuadrat]
$A.\ y = x^{2} + 4x + 2$
$B.\ y = -x^{2} - 4x + 2$
$C.\ y = x^{2} - 4x - 2$
$D.\ y = -x^{2} + 4x + 2$
$E.\ y = -x^{2} - 4x - 2$
[Fungsi Kuadrat]
Titik balik $(2, 6)$ dan melalui $(1, 5)$ artinya adalah titik puncak $(2, 6)$ dan melalui $(1, 5)$. Substitusi titik puncak dan titik yang dilalui kedalam persamaan:
$y = a(x - P)^{2} + Q$
substitusi titik puncak.
$y = a(x - 2)^{2} + 6$ .... *
untuk mendapatkan $a$, substitusi titik yang dilalui.
$5 = a(1 - 2)^{2} + 6$
$5 = a + 6$
$a = -1$
kemudian substitusi nilai $a = -1$ kedalam persamaan *
$y = -1(x - 2)^{2} + 6$
$y = -1(x^{2} - 4x + 4) + 6$
$y = -x^{2} + 4x - 4 + 6$
$y = -x^{2} + 4x + 2$ → D.
$y = a(x - P)^{2} + Q$
substitusi titik puncak.
$y = a(x - 2)^{2} + 6$ .... *
untuk mendapatkan $a$, substitusi titik yang dilalui.
$5 = a(1 - 2)^{2} + 6$
$5 = a + 6$
$a = -1$
kemudian substitusi nilai $a = -1$ kedalam persamaan *
$y = -1(x - 2)^{2} + 6$
$y = -1(x^{2} - 4x + 4) + 6$
$y = -x^{2} + 4x - 4 + 6$
$y = -x^{2} + 4x + 2$ → D.
$11.$ Suatu fungsi kuadrat berada di bawah sumbu $x$ pada selang $-2 < x < 3$ dan melalui titik $(2, -4)$. Fungsi kuadrat tersebut adalah . . . .
$A.\ y = x^{2} + x - 6$
$B.\ y = x^{2} - x + 6$
$C.\ y = x^{2} + 6x - 1$
$D.\ y = x^{2} - 6x + 1$
$E.\ y = x^{2} - x - 6$
[Fungsi Kuadrat]
$A.\ y = x^{2} + x - 6$
$B.\ y = x^{2} - x + 6$
$C.\ y = x^{2} + 6x - 1$
$D.\ y = x^{2} - 6x + 1$
$E.\ y = x^{2} - x - 6$
[Fungsi Kuadrat]
Di bawah sumbu $x$ pada selang $-2 < x < 3$ dan melalui titik $(2, -4)$, artinya kurva memotong sumbu $x$ di titik $(-2, 0)\ dan\ (3, 0)$ serta melalui titik $(2, -4)$. Substitusi titik potong sumbu x dan titik yang dilalui kedalam persamaan:
$y = a(x - x_1)(x - x_2)$
substitusi titik potong sumbu $x$ !
$y = a(x + 2)(x - 3)$ .... *
untuk mendapatkan nilai $a$, substitusi titik yang dilalui.
$-4 = a(2 + 2)(2 - 3)$
$-4 = -4a$
$a = 1$
substitusi $a = 1$ kedalam persamaan *
$y = 1.(x + 2)(x - 3)$
$y = x^{2} - x - 6$ → E.
$y = a(x - x_1)(x - x_2)$
substitusi titik potong sumbu $x$ !
$y = a(x + 2)(x - 3)$ .... *
untuk mendapatkan nilai $a$, substitusi titik yang dilalui.
$-4 = a(2 + 2)(2 - 3)$
$-4 = -4a$
$a = 1$
substitusi $a = 1$ kedalam persamaan *
$y = 1.(x + 2)(x - 3)$
$y = x^{2} - x - 6$ → E.
$12.$ Diketahui titik puncak parabola terletak pada garis $y = x + 2$. Jika sumbu simetrinya adalah $x = 2$, dan parabola melalui titik $(4, 0)$, maka persamaan parabolanya adalah . . . .
$A.\ y = x^{2} - 4x$
$B.\ y = x^{2} + 4x$
$C.\ y = -x^{2} - 4x$
$D.\ y = -x^{2} + 4x$
$E.\ y = -4x^{2} - x$
[Fungsi Kuadrat]
$A.\ y = x^{2} - 4x$
$B.\ y = x^{2} + 4x$
$C.\ y = -x^{2} - 4x$
$D.\ y = -x^{2} + 4x$
$E.\ y = -4x^{2} - x$
[Fungsi Kuadrat]
Masukkan $x = 2$ ke dalam persamaan $y = x + 2$ untuk mendapatkan koordinat titik puncak.
$y = 2 + 2$
$y = 4$
Maka koordinat titik puncak adalah $(2, 4)$ dan melalui $(4, 0)$ berarti $P = 2\ dan\ Q = 4$. Masukkan kedalam persamaan:
$y = a(x - P)^{2} + Q$
$y = a(x - 2)^{2} + 4$ .... *
untuk mendapatkan nilai $a$, masukkan titik yang dilalui ke dalam persamaan *.
$0 = a(4 - 2)^{2} + 4$
$0 = 4a + 4$
$-4 = 4a$
$a = -1$
masukkan kembali $a = -1$ ke dalam persamaan *
$y = -1(x - 2)^{2} + 4$
$y = -1(x^{2} - 4x + 4) + 4$
$y = -x^{2} + 4x - 4 + 4$
$y = -x^{2} + 4x$ → D.
$y = 2 + 2$
$y = 4$
Maka koordinat titik puncak adalah $(2, 4)$ dan melalui $(4, 0)$ berarti $P = 2\ dan\ Q = 4$. Masukkan kedalam persamaan:
$y = a(x - P)^{2} + Q$
$y = a(x - 2)^{2} + 4$ .... *
untuk mendapatkan nilai $a$, masukkan titik yang dilalui ke dalam persamaan *.
$0 = a(4 - 2)^{2} + 4$
$0 = 4a + 4$
$-4 = 4a$
$a = -1$
masukkan kembali $a = -1$ ke dalam persamaan *
$y = -1(x - 2)^{2} + 4$
$y = -1(x^{2} - 4x + 4) + 4$
$y = -x^{2} + 4x - 4 + 4$
$y = -x^{2} + 4x$ → D.
$13.$ Jika parabola memotong sumbu $x$ di titik $(-1, 0)\ dan\ (3, 0)$ serta memotong sumbu $y$ di titik $(0, -3)$, maka titik balik parabola tersebut adalah . . . .
$A.\ (1, 4)$
$B.\ (1, -4)$
$C.\ (-1, 4)$
$D.\ (-1, -4)$
$E.\ (1, 5)$
[Fungsi Kuadrat]
$A.\ (1, 4)$
$B.\ (1, -4)$
$C.\ (-1, 4)$
$D.\ (-1, -4)$
$E.\ (1, 5)$
[Fungsi Kuadrat]
Memotong sumbu $x$ di titik $(-1, 0)\ dan\ (3, 0)$ serta melalui titik $(0, -3)$.
$y = a(x - x_1)(x - x_2)$
$y = a(x + 1)(x - 3)$ .... *
masukkan titik yang dilalui.
$-3 = a(0 + 1)(0 - 3)$
$-3 = -3a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x + 1)(x - 3)$
$y = x^{2} - 2x - 3$
sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-2)}{2.1}$
$x = \dfrac{2}{2}$
$x = 1$
$y_{min} = f\left(\dfrac{-b}{2a}\right)$
$y_{min} = f(1)$
$= 1^{2} - 2.1 - 3$
$= -4$
Jadi koordinat titik puncak atau titik balik parabola adalah $(1, -4)$ → B.
$y = a(x - x_1)(x - x_2)$
$y = a(x + 1)(x - 3)$ .... *
masukkan titik yang dilalui.
$-3 = a(0 + 1)(0 - 3)$
$-3 = -3a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x + 1)(x - 3)$
$y = x^{2} - 2x - 3$
sumbu simetri:
$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-2)}{2.1}$
$x = \dfrac{2}{2}$
$x = 1$
$y_{min} = f\left(\dfrac{-b}{2a}\right)$
$y_{min} = f(1)$
$= 1^{2} - 2.1 - 3$
$= -4$
Jadi koordinat titik puncak atau titik balik parabola adalah $(1, -4)$ → B.
$14$. Jika grafik $y = x^{2} + ax + b$ mempunyai titik puncak $(1, 2)$, maka nilai $a\ dan\ b$ adalah . . . .
$A.\ a = 1,\ b = 3$
$B.\ a = -1,\ b = -3$
$C.\ a = -2,\ b = 3$
$D.\ a = 0,5,\ b = 1,5$
$E.\ a = 0,5,\ b = -1,5$
[Soal Fungsi Kuadrat UMPTN]
$A.\ a = 1,\ b = 3$
$B.\ a = -1,\ b = -3$
$C.\ a = -2,\ b = 3$
$D.\ a = 0,5,\ b = 1,5$
$E.\ a = 0,5,\ b = -1,5$
[Soal Fungsi Kuadrat UMPTN]
Karena titik puncaknya $(1, 2)$, maka sumbu simetrinya adalah $x = 1$.
$\dfrac{-b}{2a} = 1$
$\dfrac{-a}{2.1} = 1$
$a = -2$
$y_{min} = 2$
$f(1) = 2$
$1^{2} + a.1 + b = 2$
$1 - 2 + b = 2$
$b = 3$
$jadi\ a = -2,\ b = 3$ → C.
$\dfrac{-b}{2a} = 1$
$\dfrac{-a}{2.1} = 1$
$a = -2$
$y_{min} = 2$
$f(1) = 2$
$1^{2} + a.1 + b = 2$
$1 - 2 + b = 2$
$b = 3$
$jadi\ a = -2,\ b = 3$ → C.
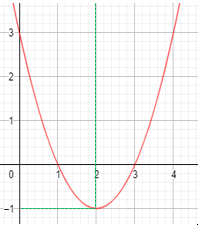
$15$. Grafik di bawah ini adalah grafik dari . . . .
$A.\ y = x^{2} - 3x + 4$
$B.\ y = x^{2} - 4x + 3$
$C.\ y = x^{2} + 4x + 3$
$D.\ y = x^{2} - 8x + 3$
$E.\ y = x^{2} - 3x + 3$
[Soal Fungsi Kuadrat UMPTN]
$A.\ y = x^{2} - 3x + 4$
$B.\ y = x^{2} - 4x + 3$
$C.\ y = x^{2} + 4x + 3$
$D.\ y = x^{2} - 8x + 3$
$E.\ y = x^{2} - 3x + 3$
[Soal Fungsi Kuadrat UMPTN]
Kurva memotong sumbu $x$ di titik $(1, 0)\ dan\ (3, 0)$ serta melalui titik $(0, 3)$.
$y = a(x - x_1)(x - x_2)$
$y = a(x - 1)(x - 3)$ .... *
$3 = a(0 - 1)(0 - 3)$
$3 = 3a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x - 1)(x - 3)$
$y = x^{2} - 4x + 3$ → B.
$y = a(x - x_1)(x - x_2)$
$y = a(x - 1)(x - 3)$ .... *
$3 = a(0 - 1)(0 - 3)$
$3 = 3a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x - 1)(x - 3)$
$y = x^{2} - 4x + 3$ → B.
16. Jika fungsi kuadrat $f(x) = 2ax^{2} + 4x + 5a$ mempunyai nilai maksimum $3$, maka $25a^{2} + 5a = . . . .$
$A.\ 2$
$B.\ 6$
$C.\ 9$
$D.\ 15$
$E.\ 30$
[Fungsi Kuadrat]
$A.\ 2$
$B.\ 6$
$C.\ 9$
$D.\ 15$
$E.\ 30$
[Fungsi Kuadrat]
$f(x) = 2ax^{2} + 4x + 5a$
$Sumbu\ simetri:$
$x = \dfrac{-b}{2a}$
$x = \dfrac{-4}{2.2a}$
$x = \dfrac{-1}{a}$
$y_{maks/min} = f\left(\dfrac{-b}{2a}\right)$
$3 = f\left(\dfrac{-1}{a}\right)$
$3 = 2a.\left(\dfrac{-1}{a}\right)^{2} + 4.\left(\dfrac{-1}{a}\right) + 5a$
$3 = \dfrac{2}{a} - \dfrac{4}{a} + 5a$
$3 = -\dfrac{2}{a} + 5a$
$3a = -2 + 5a^{2}$
$5a^{2} - 3a -2 = 0$
$(5a + 2)(a - 1) = 0$
$a = -\dfrac{2}{5}\ atau\ a = 1$.
Jika $a = 1 > 0$, yang ada adalah nilai minimum.
Jadi yang menghasilkan nilai maksimum adalah:
$a = -\dfrac{2}{5}$
$25a^{2} + 5a = 25.\left(-\dfrac{2}{5}\right)^{2} + 5.\left(-\dfrac{2}{5}\right)$
$= 25.\dfrac{4}{25} - 2$
$= 2$ → A.
$Sumbu\ simetri:$
$x = \dfrac{-b}{2a}$
$x = \dfrac{-4}{2.2a}$
$x = \dfrac{-1}{a}$
$y_{maks/min} = f\left(\dfrac{-b}{2a}\right)$
$3 = f\left(\dfrac{-1}{a}\right)$
$3 = 2a.\left(\dfrac{-1}{a}\right)^{2} + 4.\left(\dfrac{-1}{a}\right) + 5a$
$3 = \dfrac{2}{a} - \dfrac{4}{a} + 5a$
$3 = -\dfrac{2}{a} + 5a$
$3a = -2 + 5a^{2}$
$5a^{2} - 3a -2 = 0$
$(5a + 2)(a - 1) = 0$
$a = -\dfrac{2}{5}\ atau\ a = 1$.
Jika $a = 1 > 0$, yang ada adalah nilai minimum.
Jadi yang menghasilkan nilai maksimum adalah:
$a = -\dfrac{2}{5}$
$25a^{2} + 5a = 25.\left(-\dfrac{2}{5}\right)^{2} + 5.\left(-\dfrac{2}{5}\right)$
$= 25.\dfrac{4}{25} - 2$
$= 2$ → A.
$17$. Jika fungsi kuadrat $y = ax^{2} + 6x + (a + 1)$ mempunyai sumbu simetri $x = 3$, maka nilai ekstrim fungsi itu adalah . . . .
$A.\ maksimum\ 1$
$B.\ minimum\ 3$
$C.\ maksimum\ 5$
$D.\ maksimum\ 9$
$E.\ maksimum\ 18$
[Soal Fungsi Kuadrat UMPTN]
$A.\ maksimum\ 1$
$B.\ minimum\ 3$
$C.\ maksimum\ 5$
$D.\ maksimum\ 9$
$E.\ maksimum\ 18$
[Soal Fungsi Kuadrat UMPTN]
$y = ax^{2} + 6x + (a + 1)$
$Sumbu\ simetri:$
$x = \dfrac{-b}{2a}$
$3 = \dfrac{-6}{2.a}$
$6a = -6$
$a = -1$
karena $a < 0$, fungsi terbuka kebawah, yang ada adalah nilai maksimum.
fungsi menjadi: $y = -x^{2} + 6x$
$y_{maks} = f(3)$
$= -3^{2} + 6.3$
$= -9 + 18$
$= 9$ → D.
$Sumbu\ simetri:$
$x = \dfrac{-b}{2a}$
$3 = \dfrac{-6}{2.a}$
$6a = -6$
$a = -1$
karena $a < 0$, fungsi terbuka kebawah, yang ada adalah nilai maksimum.
fungsi menjadi: $y = -x^{2} + 6x$
$y_{maks} = f(3)$
$= -3^{2} + 6.3$
$= -9 + 18$
$= 9$ → D.
$18$. Grafik $y = px^{2} + (p + 2)x - p + 4$ memotong sumbu $x$ di dua titik. Batas-batas nilai $p$ yang memenuhi adalah . . . .
$A.\ p < 2\ atau\ p > -\dfrac{2}{5}$
$B.\ p < \dfrac{2}{5}\ atau\ p > 2$
$C.\ p < 2\ atau\ p > 10$
$D.\ \dfrac{2}{5} < p < 2$
$E.\ 2 < x < 10$
[Fungsi Kuadrat]
$A.\ p < 2\ atau\ p > -\dfrac{2}{5}$
$B.\ p < \dfrac{2}{5}\ atau\ p > 2$
$C.\ p < 2\ atau\ p > 10$
$D.\ \dfrac{2}{5} < p < 2$
$E.\ 2 < x < 10$
[Fungsi Kuadrat]
$y = px^{2} + (p + 2)x - p + 4$
memotong sumbu $x$ di dua titik, berarti $D > 0$.
$b^{2} - 4ac > 0$
$(p + 2)^{2} - 4.p.(-p + 4) > 0$
$p^{2} + 4p + 4 + 4p^{2} - 16p > 0$
$5p^{2} -12p + 4 > 0$
$(5p - 2)(p - 2) > 0$
$p < \dfrac{2}{5}\ atau\ p > 2$ → B.
memotong sumbu $x$ di dua titik, berarti $D > 0$.
$b^{2} - 4ac > 0$
$(p + 2)^{2} - 4.p.(-p + 4) > 0$
$p^{2} + 4p + 4 + 4p^{2} - 16p > 0$
$5p^{2} -12p + 4 > 0$
$(5p - 2)(p - 2) > 0$
$p < \dfrac{2}{5}\ atau\ p > 2$ → B.
$19$. Jika fungsi kuadrat $y = f(x)$ mencapai minimum di titik $(1, -4)$ dan $f(4) = 5$. Maka $f(x) =$ . . . .
$A.\ x^{2} + 2x + 3$
$B.\ x^{2} - 2x + 3$
$C.\ x^{2} - 2x - 3$
$D.\ -x^{2} + 2x + 3$
$E.\ -x^{2} + 2x - 3$
[Fungsi Kuadrat]
$A.\ x^{2} + 2x + 3$
$B.\ x^{2} - 2x + 3$
$C.\ x^{2} - 2x - 3$
$D.\ -x^{2} + 2x + 3$
$E.\ -x^{2} + 2x - 3$
[Fungsi Kuadrat]
Kalau soalnya diterjemahkan kedalam bahasa Indonesia yang lebih keren, artinya adalah: titik puncak $(1, -4)$ dan melalui titik $(4, 5)$.
$y = a(x - P)^{2} + Q$
$y = a(x - 1)^{2} - 4$ .... *
masukkan titik yang dilalui.
$5 = a(4 - 1)^{2} - 4$
$9 = 9a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x - 1)^{2} - 4$
$y = x^{2} - 2x + 1 - 4$
$y = x^{2} - 2x - 3$ → C.
$y = a(x - P)^{2} + Q$
$y = a(x - 1)^{2} - 4$ .... *
masukkan titik yang dilalui.
$5 = a(4 - 1)^{2} - 4$
$9 = 9a$
$a = 1$
masukkan $a = 1$ kedalam persamaan *
$y = 1.(x - 1)^{2} - 4$
$y = x^{2} - 2x + 1 - 4$
$y = x^{2} - 2x - 3$ → C.
$20$. Persamaan parabola yang titik puncaknya $(2, 1)$ dan menyinggung garis $y = 2x + 1$ adalah . . . .
$A.\ 4y - 2x^{2} + 2x = 0$
$B.\ 2y + x^{2} - 3x = 0$
$C.\ 4y + x^{2} - 4x = 0$
$D.\ 2y - 2x^{2} + 3x = 0$
$E.\ 2y - x^{2} + 2x = 0$
[Fungsi Kuadrat]
$A.\ 4y - 2x^{2} + 2x = 0$
$B.\ 2y + x^{2} - 3x = 0$
$C.\ 4y + x^{2} - 4x = 0$
$D.\ 2y - 2x^{2} + 3x = 0$
$E.\ 2y - x^{2} + 2x = 0$
[Fungsi Kuadrat]
Puncak $(2, 1)$ berarti persamaan parabola adalah: $y = a(x - P)^{2} + Q$
$y = a(x - 2)^{2} + 1$ .... *
$y = a(x^{2} - 4x + 4) + 1$
$y = ax^{2} - 4ax + 4a + 1$
Parabola menyinggung garis $y = 2x + 1$, sehingga:
$ax^{2} - 4ax + 4a + 1 = 2x + 1$
$ax^{2} - 4ax - 2x + 4a = 0$
$ax^{2} - (4a + 2)x + 4a = 0$
karena bersinggungan, maka $D = 0$.
$(-(4a + 2))^{2} - 4.a.4a = 0$
$16a^{2} + 16a + 4 - 16a^{2} = 0$
$16a + 4 = 0$
$a = -\dfrac{1}{4}$
masukkan nila $a = -\dfrac{1}{4}$ kedalam persamaan *
$y = -\dfrac{1}{4}(x - 2)^{2} + 1$
$4y = -(x - 2)^{2} + 4$
$4y = -(x^{2} - 4x + 4) + 4$
$4y = -x^{2} + 4x - 4 + 4$
$4y = -x^{2} + 4x$
$4y + x^{2} - 4x = 0$ → C.
$y = a(x - 2)^{2} + 1$ .... *
$y = a(x^{2} - 4x + 4) + 1$
$y = ax^{2} - 4ax + 4a + 1$
Parabola menyinggung garis $y = 2x + 1$, sehingga:
$ax^{2} - 4ax + 4a + 1 = 2x + 1$
$ax^{2} - 4ax - 2x + 4a = 0$
$ax^{2} - (4a + 2)x + 4a = 0$
karena bersinggungan, maka $D = 0$.
$(-(4a + 2))^{2} - 4.a.4a = 0$
$16a^{2} + 16a + 4 - 16a^{2} = 0$
$16a + 4 = 0$
$a = -\dfrac{1}{4}$
masukkan nila $a = -\dfrac{1}{4}$ kedalam persamaan *
$y = -\dfrac{1}{4}(x - 2)^{2} + 1$
$4y = -(x - 2)^{2} + 4$
$4y = -(x^{2} - 4x + 4) + 4$
$4y = -x^{2} + 4x - 4 + 4$
$4y = -x^{2} + 4x$
$4y + x^{2} - 4x = 0$ → C.
Demikianlah Soal dan Pembahasan Fungsi Kuadrat. Selamat belajar !


no. 4 jawabannya 2 bukan ngatif 2
ReplyDeleteanda kurang teliti
Delete