Daftar isi
1. Pengertian Vektor
Soal dan Pembahasan Vektor Matematika SMA kelas 10. Sebelum kita masuk ke Soal dan Pembahasan vektor, kita akan melakukan review singkat tentang vektor matematika SMA kelas 10. Besaran vektor adalah suatu besaran yang mempunyai besar dan arah, seperti kecepatan, percepatan, gaya, berat dan lain-lain.Besaran skalar adalah suatu besaran yang hanya mempunyai besar saja, seperti panjang, lebar, massa, volume, dan lain-lain. Vektor yang akan dibahas di sini adalah vektor pada bidang yang dinotasikan dengan $\overrightarrow{a} = x\overrightarrow{i} + y\overrightarrow{j}$ dan vektor pada ruang yang dinotasikan dengan $\overrightarrow{a} = x\overrightarrow{i} + y\overrightarrow{j} + z\overrightarrow{k} $
1.1. Geometri Vektor
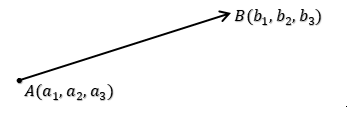
Secara geometris vektor dilukiskan sebagai anak panah dengan titik pangkal $A(a_1,\ a_2,\ a_3)$ dan titik ujung $B(b_1,\ b_2,\ b_3)$.
Lihat gambar!
1.2. Notasi Vektor
Untuk menuliskan vektor kita dapat menggunakan salah satu notasi seperti: $\overline{a}$, $\overrightarrow{a}$, $\overline{A}$, $\overrightarrow{A}$, $\overline{AB}$, dan $\overrightarrow{AB}$.
1.3. Bentuk Vektor
Vektor dapat dinyatakan dalam bentuk vektor baris, vektor basis,
dan vektor kolom.
a. Vektor baris: $\overline{a} = (a_1,\ a_2,\ a_3)$
b. Vektor basis: $\overline{a} = a_1\overrightarrow{i} + a_2\overrightarrow{j} + a_3\overrightarrow{k}$
c. Vektor kolom: $\overline{a} = \begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}$
1.4. Vektor Dengan Pangkal A dan Ujung B
Vektor dengan titik pangkal $A(a_1,\ a_2,\ a_3)$ dan titik ujung $B(b_1,\ b_2,\ b_3)$ dinotasikan dengan $\overline{AB}$, dengan
$\overline{AB} = \begin{pmatrix}b_1 - a_1\\ b_2 - a_2\\ b_3 - a_3\end{pmatrix}$
2. Jenis-jenis Vektor
2.1. Vektor NolSebuah vektor yang titik pangkal dan titik ujungnya berimpit (sama) disebut vektor nol, yang dinotasikan dengan $\overrightarrow{0}$. Vektor nol memiliki panjang nol dengan arah tak tentu. Contoh: $\overrightarrow{AA}$, $\overrightarrow{BB}$, dan lain-lain.
2.2. Vektor Satuan
Vektor satuan adalah vektor yang panjangnya satu satuan, ditulis $\hat{a}$ yang didefinisikan dengan: $\hat{a} = \dfrac{\overline{a}}{|\overline{a}|}$
3. Operasi Pada Vektor
3.1. Penjumlahan Dua Vektor
A. Secara geometris.1. Dengan metode segitiga.
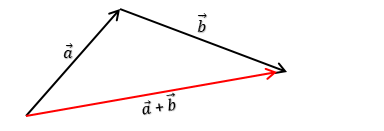
Letakkan pangkal dari salah satu vektor ke ujung dari vektor yang lain, kemudian hubungkan pangkal dari vektor pertama dengan ujung dari vektor kedua.
Perhatikan gambar!
2. Dengan metode jajargenjang.
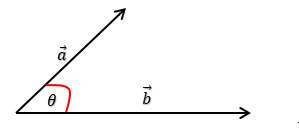
Resultan $\overline{a}$ dan $\overline{b}$ adalah diagonal dari jajargenjang yang dibentuk oleh $\overline{a}$ dan $\overline{b}$.
Perhatikan gambar!
Penjumlahan dua vektor memiliki sifat-sifat yaitu:
(i). Sifat komutatif (pertukaran):
$\overline{a} + \overline{b} = \overline{b} + \overline{a}$
(ii). Sifat assosiatif (pengelompokan):
$(\overline{a} + \overline{b}) + \overline{c} = \overline{a} + (\overline{b} + \overline{c})$
(iii). Unsur identitas yaitu $\overline{0} = (0, 0, 0)$
$\overline{a} + \overline{0} = \overline{a}$
(iv). Invers tambah atau invers aditif.
invers tambah dari vektor $\overline{a}$ adalah $-\overline{a}$
$\overline{a} + (-\overline{a}) = \overline{0}$
B. Secara analitis
Jika $\overline{a} = (a_1, a_2, a_3)$ dan $\overline{b} = (b_1, b_2, b_3)$, maka
$(i).\ \overline{a} + \overline{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3)$
$(ii).\ |\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta$
3.2. Pengurangan Dua Vektor
A. Secara geometris.1. Dengan metode segitiga.
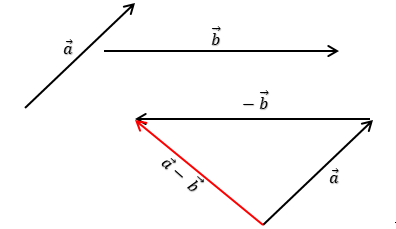
Arah vektor yang dikurangkan dibalik dan pangkalnya diletakkan pada ujung vektor yang lain.
Perhatikan gambar!
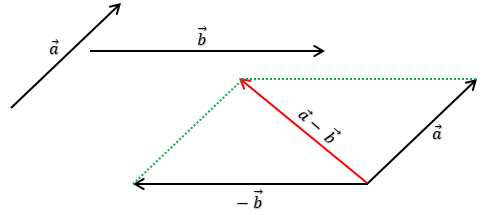
2. Dengan metode jajargenjang.
B. Secara analitis.
Jika $\overline{a} = (a_1, a_2, a_3)$ dan $\overline{b} = (b_1, b_2, b_3)$, maka:
$(i).\ \overline{a} - \overline{b} = (a_1 - b_1, a_2 - b_2, a_3 - b_3)$
$(ii).\ |\overrightarrow{a} - \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta$
3.3. Perkalian Dua Vektor
A. Perkalian skalarMisalkan vektor $\overrightarrow{a} = \begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}$ dan $k$ merupakan bilangan real,
maka $k\overrightarrow{a} = k\begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}$
B. Perkalian titik atau dot
Jika vektor $\overrightarrow{a} = (a_1, a_2, a_3)$ dan vektor $\overrightarrow{b} = (b_1, b_2, b_3)$, maka:
$⇒$ $\overrightarrow{a}.\overrightarrow{b} = (a_1.b_1 + a_2.b_2 + a_3.b_3)$
$⇒$ $\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos\theta$
dimana θ adalah sudut antara vektor $\overrightarrow{a}$ dan $\overrightarrow{b}$
Lihat gambar!
Sifat-sifat perkalian skalar dua vektor
1. Sifat komutatif: $\overrightarrow{a}.\overrightarrow{b} =\overrightarrow{b}. \overrightarrow{a}$
2. $m(\overrightarrow{a}.\overrightarrow{b} = (m\overrightarrow{a}).\overrightarrow{b} = \overrightarrow{a}.(m\overrightarrow{b})$
3. Sifat distributif:
(I). $\overrightarrow{a}(\overrightarrow{b} + \overrightarrow{c}) = \overrightarrow{a}.\overrightarrow{b} + \overrightarrow{a}.\overrightarrow{c}$
(II). $(\overrightarrow{a} + \overrightarrow{b})\overrightarrow{c} = \overrightarrow{a}.\overrightarrow{c} + \overrightarrow{b}\overrightarrow{c}$
4. $\overrightarrow{a}.\overrightarrow{a} = |\overrightarrow{a}|^2$
C. Perkalian silang
Jika vektor $\overrightarrow{a} = (a_1, a_2, a_3)$ dan vektor $\overrightarrow{b} = (b_1, b_2, b_3)$, maka:
perkalian silang ditulis $\overrightarrow{a}$ x $\overrightarrow{b}$ dirumuskan:
$\overrightarrow{a} \ \times\ \overrightarrow{b} = \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3
\end{vmatrix}$
$= (a_2b_3 - a_3b_2)\hat{i} + (a_3b_1 - a_1b_3)\hat{j} + (a_1b_2 - b_2a_1)\hat{k}$
3.4. Perbandingan Koordinat dan Perbandingan Vektor
Lihat gambar!$x = \dfrac{mx_2 + nx_1}{m + n}$
$y = \dfrac{my_2 + ny_1}{m + n}$
$z = \dfrac{mz_2 + nz_1}{m + n}$
$\overrightarrow{c} = \dfrac{n\overrightarrow{a} + m\overrightarrow{b}}{m + n}$
3.5. Proyeksi Orthogonal Vektor $\overrightarrow{a}$ pada Vektor $\overrightarrow{b}$
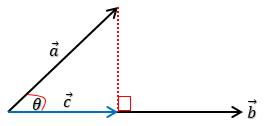
Misalkan vektor $\overrightarrow{a}$ dan vektor $\overrightarrow{b}$ adalah vektor-vektor sembarang pada bidang atau pada ruang, dan vektor $\overrightarrow{c}$ adalah proyeksi vektor $\overrightarrow{a}$ pada vektor $\overrightarrow{b}$.A. Proyeksi skalar orthogonal dari vektor $\overrightarrow{a}$ pada arah vektor $\overrightarrow{b}$, adalah $\overrightarrow{c}$ yang ditentukan oleh:
$|\overrightarrow{c}| = \dfrac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{b}|}$
B. Proyeksi vektor orthogonal dari vektor $\overrightarrow{a}$ pada arah vektor $\overrightarrow{b}$, adalah $\overrightarrow{c}$ yang ditentukan oleh:
$\overrightarrow{c} = \dfrac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{b}|^2}\overrightarrow{b}$
3.6. Rumus Panjang Vektor
Besar dan panjang vektor ditulis sebagai |$\overline{a}$| atau |$\overrightarrow{a}$|, sedangkan panjang vektor $\overrightarrow{AB}$ ditulis sebagai |$\overrightarrow{AB}$| atau |$\overline{AB}$|. Misalkan $\overline{a} = (a_1, a_2, a_3)$ maka panjang vektor $\overline{a}$ didefinisikan sebagai: |$\overline{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$3.7. Kesamaan Dua Vektor
Dua vektor disebut sama jika panjang dan arah vektor sama. Vektor tidak tergantung pada letaknya, tetapi tergantung pada panjang dan arahnya.Misalkan vektor $\overrightarrow{a} = (a_1, a_2, a_3)$ dan vektor $\overrightarrow{b} = (b_1, b_2, b_3)$.
$\overrightarrow{a} = \overrightarrow{b}$ jika $a_1 = b_1, a_2 = b_2, a_3 = b_3$
4. Pengertian Vektor posisi
Vektor posisi adalah vektor yang berpangkal di titik asal O(0, 0). Vektor posisi dari titik A, B, C, dan D sering ditulis $\overline{a}$, $\overline{b}$, $\overline{c}$, $\overline{d}$ dan seterusnya.$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$
$\overrightarrow{AB} = \overrightarrow{b} - \overrightarrow{a}$
5. Pengertian Vektor Koliner
Tiga buah titik A, B, dan C segaris (koliner) jika dan hanya jika $\overrightarrow{AB} = k\overrightarrow{BC}$ dengan k bilangan real tidak nol.6. Contoh Soal Vektor Matematika dan Pembahasan
$1$. Diketahui vektor $\overrightarrow{a} = \begin{pmatrix} 3\\ -2\end{pmatrix}$, vektor $\overrightarrow{b} = \begin{pmatrix} 4\\ 1\end{pmatrix}$,
dan vektor $\overrightarrow{c} = \begin{pmatrix} -2\\ -1\end{pmatrix}$. Jika $2\overrightarrow{a} - 3\overrightarrow{b} + k\overrightarrow{c} = \begin{pmatrix} 0\\ -4\end{pmatrix}$, dengan $k$ bilangan real,
maka nilai $k$ adalah . . . .
$A.\ -5$
$B.\ -3$
$C.\ -1$
$D.\ 1$
$E.\ 3$
dan vektor $\overrightarrow{c} = \begin{pmatrix} -2\\ -1\end{pmatrix}$. Jika $2\overrightarrow{a} - 3\overrightarrow{b} + k\overrightarrow{c} = \begin{pmatrix} 0\\ -4\end{pmatrix}$, dengan $k$ bilangan real,
maka nilai $k$ adalah . . . .
$A.\ -5$
$B.\ -3$
$C.\ -1$
$D.\ 1$
$E.\ 3$
$2\begin{pmatrix} 3\\ -2\end{pmatrix} - 3\begin{pmatrix} 4\\ 1\end{pmatrix} + k\begin{pmatrix} -2\\ -1\end{pmatrix} = \begin{pmatrix} 0\\ -4\end{pmatrix}$
$\begin{pmatrix} 6\\ -4\end{pmatrix} - \begin{pmatrix} 12\\ 3\end{pmatrix} + \begin{pmatrix} -2k\\ -k\end{pmatrix} = \begin{pmatrix} 0\\ -4\end{pmatrix}$
$\begin{pmatrix} -6 - 2k\\ -7 - k\end{pmatrix} = \begin{pmatrix} 0\\ -4\end{pmatrix}$
Didapat persamaan:
$-6 -2k = 0$
$k = -3$ → B.
$\begin{pmatrix} 6\\ -4\end{pmatrix} - \begin{pmatrix} 12\\ 3\end{pmatrix} + \begin{pmatrix} -2k\\ -k\end{pmatrix} = \begin{pmatrix} 0\\ -4\end{pmatrix}$
$\begin{pmatrix} -6 - 2k\\ -7 - k\end{pmatrix} = \begin{pmatrix} 0\\ -4\end{pmatrix}$
Didapat persamaan:
$-6 -2k = 0$
$k = -3$ → B.
$2$. Diketahui titik $P(1, 7)$ dan titik $Q(4, 1)$. Titik $R$ adalah titik pada garis hubung $PQ$ sehingga $\overrightarrow{PR} = \dfrac{1}{3}PQ$. Maka koordinat titik $R$ adalah . . . .
$A.\ (2, 5)$
$B.\ (5, 2)$
$C.\ (3, 4)$
$D.\ (2, 3)$
$E.\ (3, 2)$
$A.\ (2, 5)$
$B.\ (5, 2)$
$C.\ (3, 4)$
$D.\ (2, 3)$
$E.\ (3, 2)$
$\overrightarrow{PQ} = \overrightarrow{q} - \overrightarrow{p}$
= $\begin{pmatrix} 4\\ 1\end{pmatrix} - \begin{pmatrix} 1\\ 7\end{pmatrix}$
= $\begin{pmatrix} 3\\ -6\end{pmatrix}$
$\overrightarrow{PR} = \dfrac{1}{3}\overrightarrow{PQ}$
= $\dfrac{1}{3}\begin{pmatrix} 3\\ -6\end{pmatrix}$
= $\begin{pmatrix} 1\\ -2\end{pmatrix}$
Misalkan koordinat dari titik R adalah (x, y) sehingga $\overrightarrow{r} = \begin{pmatrix} x\\ y\end{pmatrix}$
$\overrightarrow{PR} = \overrightarrow{r} - \overrightarrow{p}$
$\begin{pmatrix} 1\\ -2\end{pmatrix} = \begin{pmatrix} x\\ y\end{pmatrix} - \begin{pmatrix} 1\\ 7\end{pmatrix}$
Didapat dua persamaan
Pertama:
$1 = x - 1$
$x = 2$
Kedua:
$-2 = y - 7$
$y = 5$
Jadi koordinat titik R adalah (2, 5) → A.
Note:
$\overrightarrow{p}$ adalah vektor posisi dari titik P.
$\overrightarrow{q}$ adalah vektor posisi dari titik Q.
$\overrightarrow{r}$ adalah vektor posisi dari titik R.
= $\begin{pmatrix} 4\\ 1\end{pmatrix} - \begin{pmatrix} 1\\ 7\end{pmatrix}$
= $\begin{pmatrix} 3\\ -6\end{pmatrix}$
$\overrightarrow{PR} = \dfrac{1}{3}\overrightarrow{PQ}$
= $\dfrac{1}{3}\begin{pmatrix} 3\\ -6\end{pmatrix}$
= $\begin{pmatrix} 1\\ -2\end{pmatrix}$
Misalkan koordinat dari titik R adalah (x, y) sehingga $\overrightarrow{r} = \begin{pmatrix} x\\ y\end{pmatrix}$
$\overrightarrow{PR} = \overrightarrow{r} - \overrightarrow{p}$
$\begin{pmatrix} 1\\ -2\end{pmatrix} = \begin{pmatrix} x\\ y\end{pmatrix} - \begin{pmatrix} 1\\ 7\end{pmatrix}$
Didapat dua persamaan
Pertama:
$1 = x - 1$
$x = 2$
Kedua:
$-2 = y - 7$
$y = 5$
Jadi koordinat titik R adalah (2, 5) → A.
Note:
$\overrightarrow{p}$ adalah vektor posisi dari titik P.
$\overrightarrow{q}$ adalah vektor posisi dari titik Q.
$\overrightarrow{r}$ adalah vektor posisi dari titik R.
$3$. Jika vektor $\overrightarrow{a} = \begin{pmatrix} 2\\ 3\end{pmatrix}$, vektor $\overrightarrow{b} = \begin{pmatrix} 3\\ 9\end{pmatrix}$ dan
$\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}$. Vektor satuan dari vektor $\overrightarrow{c}$ adalah . . . .
$A.\ \dfrac{1}{13}\begin{pmatrix} 5\\ 13\end{pmatrix}$
$B.\ \dfrac{1}{13}\begin{pmatrix} 5\\ 12\end{pmatrix}$
$C.\ \dfrac{1}{5}\begin{pmatrix} 12\\ 13\end{pmatrix}$
$D.\ \dfrac{1}{12}\begin{pmatrix} 5\\ 13\end{pmatrix}$
$E.\ \dfrac{1}{12}\begin{pmatrix} 13\\ 5\end{pmatrix}$
$\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}$. Vektor satuan dari vektor $\overrightarrow{c}$ adalah . . . .
$A.\ \dfrac{1}{13}\begin{pmatrix} 5\\ 13\end{pmatrix}$
$B.\ \dfrac{1}{13}\begin{pmatrix} 5\\ 12\end{pmatrix}$
$C.\ \dfrac{1}{5}\begin{pmatrix} 12\\ 13\end{pmatrix}$
$D.\ \dfrac{1}{12}\begin{pmatrix} 5\\ 13\end{pmatrix}$
$E.\ \dfrac{1}{12}\begin{pmatrix} 13\\ 5\end{pmatrix}$
$\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}$
= $\begin{pmatrix} 2\\ 3\end{pmatrix} + \begin{pmatrix} 3\\ 9\end{pmatrix}$
= $\begin{pmatrix} 5\\ 12\end{pmatrix}$
$|\overrightarrow{c}|^2 = 5^2 + 12^2$
$|\overrightarrow{c}|^2 = 169$
$|\overrightarrow{c}| = 13$
$\hat{c} = \dfrac{\overrightarrow{c}}{|\overrightarrow{c}|}$
= $\dfrac{1}{13}\begin{pmatrix} 5\\ 12\end{pmatrix}$ → B.
= $\begin{pmatrix} 2\\ 3\end{pmatrix} + \begin{pmatrix} 3\\ 9\end{pmatrix}$
= $\begin{pmatrix} 5\\ 12\end{pmatrix}$
$|\overrightarrow{c}|^2 = 5^2 + 12^2$
$|\overrightarrow{c}|^2 = 169$
$|\overrightarrow{c}| = 13$
$\hat{c} = \dfrac{\overrightarrow{c}}{|\overrightarrow{c}|}$
= $\dfrac{1}{13}\begin{pmatrix} 5\\ 12\end{pmatrix}$ → B.
$4$. Diberikan titik-titik $A(1, 3),\ B(2, 5),\ C(-1, 2)$. Ruas garis berarah $\overrightarrow{AB}$ dan $\overrightarrow{BC}$ berturut-turut mewakili vektor $\overrightarrow{u}$ dan vektor $\overrightarrow{v}$. Maka nilai dari $(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{u}$ = . . . .
$A.\ -9$
$B.\ -4$
$C.\ 1$
$D.\ 4$
$E.\ 9$
$A.\ -9$
$B.\ -4$
$C.\ 1$
$D.\ 4$
$E.\ 9$
$\overrightarrow{AB} = \overrightarrow{u} = \overrightarrow{b} - \overrightarrow{a}$
= $\begin{pmatrix} 2\\ 5\end{pmatrix} - \begin{pmatrix} 1\\ 3\end{pmatrix}$
= $\begin{pmatrix} 1\\ 2\end{pmatrix}$
$\overrightarrow{BC} = \overrightarrow{v} = \overrightarrow{c} - \overrightarrow{b}$
= $\begin{pmatrix} -1\\ 2\end{pmatrix} - \begin{pmatrix} 2\\ 5\end{pmatrix}$
= $\begin{pmatrix} -3\\ -3\end{pmatrix}$
$(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{u} = \overrightarrow{u}.\overrightarrow{u} + \overrightarrow{v}.\overrightarrow{u}$
= $\begin{pmatrix} 1\\ 2\end{pmatrix}.\begin{pmatrix} 1\\ 2\end{pmatrix} + \begin{pmatrix} -3\\ -3\end{pmatrix}.\begin{pmatrix} 1\\ 2\end{pmatrix}$
= $5 - 9$
= $-4$ → B.
Note:
$\overrightarrow{a}$ adalah vektor posisi dari titik A.
$\overrightarrow{b}$ adalah vektor posisi dari titik B.
$\overrightarrow{c}$ adalah vektor posisi dari titik C.
= $\begin{pmatrix} 2\\ 5\end{pmatrix} - \begin{pmatrix} 1\\ 3\end{pmatrix}$
= $\begin{pmatrix} 1\\ 2\end{pmatrix}$
$\overrightarrow{BC} = \overrightarrow{v} = \overrightarrow{c} - \overrightarrow{b}$
= $\begin{pmatrix} -1\\ 2\end{pmatrix} - \begin{pmatrix} 2\\ 5\end{pmatrix}$
= $\begin{pmatrix} -3\\ -3\end{pmatrix}$
$(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{u} = \overrightarrow{u}.\overrightarrow{u} + \overrightarrow{v}.\overrightarrow{u}$
= $\begin{pmatrix} 1\\ 2\end{pmatrix}.\begin{pmatrix} 1\\ 2\end{pmatrix} + \begin{pmatrix} -3\\ -3\end{pmatrix}.\begin{pmatrix} 1\\ 2\end{pmatrix}$
= $5 - 9$
= $-4$ → B.
Note:
$\overrightarrow{a}$ adalah vektor posisi dari titik A.
$\overrightarrow{b}$ adalah vektor posisi dari titik B.
$\overrightarrow{c}$ adalah vektor posisi dari titik C.
$5$. Jika $\overrightarrow{p}$, $\overrightarrow{q}$, dan $\overrightarrow{s}$ berturut-turut adalah vektor posisi titik-titik sudut jajaran genjang PQRS dengan PQ sejajar SR, maka $\overrightarrow{s}$ = . . . .
$A.\ -\overrightarrow{p} + \overrightarrow{q} +\overrightarrow{r}$
$B.\ -\overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$
$C.\ \overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$
$D.\ \overrightarrow{p} - \overrightarrow{q} - \overrightarrow{r}$
$E.\ \overrightarrow{p} + \overrightarrow{q} + \overrightarrow{r}$
[Soal UM UGM]
$A.\ -\overrightarrow{p} + \overrightarrow{q} +\overrightarrow{r}$
$B.\ -\overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$
$C.\ \overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$
$D.\ \overrightarrow{p} - \overrightarrow{q} - \overrightarrow{r}$
$E.\ \overrightarrow{p} + \overrightarrow{q} + \overrightarrow{r}$
[Soal UM UGM]
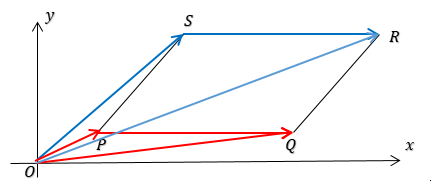
Perhatikan gambar!
PQ sejajar SR dan sama panjang, berarti $\overrightarrow{SR} = \overrightarrow{PQ} = \overrightarrow{q} - \overrightarrow{p}$.
Lihat $\Delta OSR$ dan perhatikan vektor posisi dari titik S dan titik R !
$\overrightarrow{SR} = \overrightarrow{r} - \overrightarrow{s}$
$\overrightarrow{q} - \overrightarrow{p} = \overrightarrow{r} - \overrightarrow{s}$
$\overrightarrow{s} = \overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$ → C.
PQ sejajar SR dan sama panjang, berarti $\overrightarrow{SR} = \overrightarrow{PQ} = \overrightarrow{q} - \overrightarrow{p}$.
Lihat $\Delta OSR$ dan perhatikan vektor posisi dari titik S dan titik R !
$\overrightarrow{SR} = \overrightarrow{r} - \overrightarrow{s}$
$\overrightarrow{q} - \overrightarrow{p} = \overrightarrow{r} - \overrightarrow{s}$
$\overrightarrow{s} = \overrightarrow{p} - \overrightarrow{q} + \overrightarrow{r}$ → C.
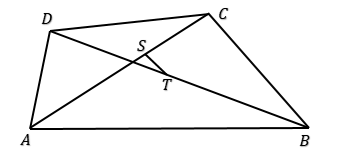
$6$. Pada segiempat sembarang ABCD, S dan T masing-masing adalah titik tengah AC dan BD. Jika $\overrightarrow{u} = \overrightarrow{ST}$, maka $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD}$ dapat dinyatakan dalam $\overrightarrow{u}$ sebagai . . . .
$A.\ \dfrac{1}{4}\overrightarrow{u}$
$B.\ \dfrac{1}{2}\overrightarrow{u}$
$C.\ \overrightarrow{u}$
$D.\ 2\overrightarrow{u}$
$E.\ 4\overrightarrow{u}$
[Soal UMPTN]
$A.\ \dfrac{1}{4}\overrightarrow{u}$
$B.\ \dfrac{1}{2}\overrightarrow{u}$
$C.\ \overrightarrow{u}$
$D.\ 2\overrightarrow{u}$
$E.\ 4\overrightarrow{u}$
[Soal UMPTN]
Ingat rumus perbandingan ruas garis dan vektor !
Lihat $\Delta ABD$ dan $\Delta BCD$ ! Karena BT = DT, maka:
$\overrightarrow{AT} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD})$
$\overrightarrow{CT} = {1\over 2}(\overrightarrow{CB} + \overrightarrow{CD})$
$\overrightarrow{AT} + \overrightarrow{CT} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD})$ . . . . (1)
Ingat penjumlahan vektor dengan metode segitiga !
$\overrightarrow{AT} = \overrightarrow{AS} + \overrightarrow{ST}$
$\overrightarrow{CT} = \overrightarrow{CS} + \overrightarrow{ST}$
$\overrightarrow{AS}$ dan $\overrightarrow{CS}$ adalah dua vektor yang sama dan berlawanan arah.
$\overrightarrow{AS} + \overrightarrow{CS} = 0$
$\overrightarrow{AT} + \overrightarrow{CT} = \overrightarrow{AS} + \overrightarrow{ST} + \overrightarrow{CS} + \overrightarrow{ST}$
$\overrightarrow{AT} + \overrightarrow{CT} = 2\overrightarrow{ST}$ . . . . (2).
Dari persamaan (1) dan (2)
$2\overrightarrow{ST} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD})$
$4\overrightarrow{ST} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD}$ → E.
Lihat $\Delta ABD$ dan $\Delta BCD$ ! Karena BT = DT, maka:
$\overrightarrow{AT} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD})$
$\overrightarrow{CT} = {1\over 2}(\overrightarrow{CB} + \overrightarrow{CD})$
$\overrightarrow{AT} + \overrightarrow{CT} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD})$ . . . . (1)
Ingat penjumlahan vektor dengan metode segitiga !
$\overrightarrow{AT} = \overrightarrow{AS} + \overrightarrow{ST}$
$\overrightarrow{CT} = \overrightarrow{CS} + \overrightarrow{ST}$
$\overrightarrow{AS}$ dan $\overrightarrow{CS}$ adalah dua vektor yang sama dan berlawanan arah.
$\overrightarrow{AS} + \overrightarrow{CS} = 0$
$\overrightarrow{AT} + \overrightarrow{CT} = \overrightarrow{AS} + \overrightarrow{ST} + \overrightarrow{CS} + \overrightarrow{ST}$
$\overrightarrow{AT} + \overrightarrow{CT} = 2\overrightarrow{ST}$ . . . . (2).
Dari persamaan (1) dan (2)
$2\overrightarrow{ST} = {1\over 2}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD})$
$4\overrightarrow{ST} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CB} + \overrightarrow{CD}$ → E.
$7$. Jika $\overrightarrow{a} = (2, k)$ dan $\overrightarrow{b} = (3, 5)$ dan $\angle (\overrightarrow{a}, \overrightarrow{b}) = \dfrac{\pi}{4}$ maka
konstanta possitif $k$ adalah . . . .
$A.\ \dfrac{1}{4}$
$B.\ \dfrac{1}{2}$
$C.\ 2$
$D.\ 4$
$E.\ 8$
[Soal UMPTN]
konstanta possitif $k$ adalah . . . .
$A.\ \dfrac{1}{4}$
$B.\ \dfrac{1}{2}$
$C.\ 2$
$D.\ 4$
$E.\ 8$
[Soal UMPTN]
Ingat perkalian dua vektor !
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos\ \theta$
$(2, k).(3, 5) = \sqrt{2^2 + k^2}.\sqrt{3^2 + 5^2}.cos\ \dfrac{\pi}{4}$
$6 + 5k = \sqrt{4 + k^2}.\sqrt{34}.\dfrac{1}{2}\sqrt{2}$
$(6 + 5k)^2 = (k^2 + 4).34.\dfrac{1}{2}$
$25k^2 + 60k + 36 = 17k^2 + 68$
$8k^2 + 60k - 32 = 0$
$2k^2 + 15k - 8 = 0$
$(k + 8)(2k - 1) = 0$
$k = -8\ atau\ k = \dfrac{1}{2}$ → B.
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos\ \theta$
$(2, k).(3, 5) = \sqrt{2^2 + k^2}.\sqrt{3^2 + 5^2}.cos\ \dfrac{\pi}{4}$
$6 + 5k = \sqrt{4 + k^2}.\sqrt{34}.\dfrac{1}{2}\sqrt{2}$
$(6 + 5k)^2 = (k^2 + 4).34.\dfrac{1}{2}$
$25k^2 + 60k + 36 = 17k^2 + 68$
$8k^2 + 60k - 32 = 0$
$2k^2 + 15k - 8 = 0$
$(k + 8)(2k - 1) = 0$
$k = -8\ atau\ k = \dfrac{1}{2}$ → B.
$8$. Jika $\overrightarrow{OA} = (1, 2)$, $\overrightarrow{OB} = (4, 2)$ dan $\theta = \angle (\overrightarrow{OA}, \overrightarrow{OB})$,
maka tan $\theta$ = . . . .
$A.\ \dfrac35$
$B.\ \dfrac34$
$C.\ \dfrac43$
$D.\ \dfrac{9}{16}$
$E.\ \dfrac{16}{9}$
maka tan $\theta$ = . . . .
$A.\ \dfrac35$
$B.\ \dfrac34$
$C.\ \dfrac43$
$D.\ \dfrac{9}{16}$
$E.\ \dfrac{16}{9}$
Ingat perkalian vektor !
$\overrightarrow{OA}.\overrightarrow{OB} = |\overrightarrow{OA}|.|\overrightarrow{OB}|.cos \theta$
$(1, 2).(4, 2) = \sqrt{1^2 + 2^2}.\sqrt{4^2 + 2^2}.cos \theta$
$4 + 4 = \sqrt{5}.\sqrt{20}.cos \theta$
$8 = \sqrt{100}.cos \theta$
$8 = 10.cos \theta$
$cos\ \theta = \dfrac{4}{5}$
Perhatikan segitiga siku-siku dibawah !
Dengan menggunakan segitiga siku-siku didapat
$tan\ \theta = \dfrac{3}{4}$ → B.
$\overrightarrow{OA}.\overrightarrow{OB} = |\overrightarrow{OA}|.|\overrightarrow{OB}|.cos \theta$
$(1, 2).(4, 2) = \sqrt{1^2 + 2^2}.\sqrt{4^2 + 2^2}.cos \theta$
$4 + 4 = \sqrt{5}.\sqrt{20}.cos \theta$
$8 = \sqrt{100}.cos \theta$
$8 = 10.cos \theta$
$cos\ \theta = \dfrac{4}{5}$
Perhatikan segitiga siku-siku dibawah !
Dengan menggunakan segitiga siku-siku didapat
$tan\ \theta = \dfrac{3}{4}$ → B.
$9$. Diketahui persegi panjang OACB dan D titik tengah OA, CD memotong diagonal AB di P. Jika $\overrightarrow{OA} = \overrightarrow{a}$ dan $\overrightarrow{OB} = \overrightarrow{b}$, maka $\overrightarrow{OP}$ dapat dinyatakan sebagai . . . .
$A.\ \dfrac{1}{2}(\overrightarrow{a} + \overrightarrow{b})$
$B.\ \dfrac{1}{3}(\overrightarrow{a} + \overrightarrow{b})$
$C.\ \dfrac{2}{3}\overrightarrow{a} + \dfrac{1}{3}\overrightarrow{b}$
$D.\ \dfrac{1}{3}\overrightarrow{a} + \dfrac{2}{3}\overrightarrow{b}$
$E.\ \dfrac{1}{2}\overrightarrow{a} + \dfrac{2}{3}\overrightarrow{b}$
[Soal SPMB]
$A.\ \dfrac{1}{2}(\overrightarrow{a} + \overrightarrow{b})$
$B.\ \dfrac{1}{3}(\overrightarrow{a} + \overrightarrow{b})$
$C.\ \dfrac{2}{3}\overrightarrow{a} + \dfrac{1}{3}\overrightarrow{b}$
$D.\ \dfrac{1}{3}\overrightarrow{a} + \dfrac{2}{3}\overrightarrow{b}$
$E.\ \dfrac{1}{2}\overrightarrow{a} + \dfrac{2}{3}\overrightarrow{b}$
[Soal SPMB]
Perhatikan gambar !
Segitiga ADP sebangun dengan segitiga BCP
$\dfrac{AD}{BC} = \dfrac{AP}{BP}$
$\dfrac{1}{2} = \dfrac{AP}{BP}$
$AP : BP = 1 : 2$
Perhatikan segitiga OAB, dan ingat perbandingan ruas garis dan vektor !
$\overrightarrow{OP} = \dfrac{2\overrightarrow{OA} + \overrightarrow{OB}}{2 + 1 }$
$\overrightarrow{OP} = \dfrac{2\overrightarrow{a} + \overrightarrow{b}}{3}$
$\overrightarrow{OP} = \dfrac{2}{3}\overrightarrow{a} + \dfrac{1}{3}\overrightarrow{b}$ → C.
Segitiga ADP sebangun dengan segitiga BCP
$\dfrac{AD}{BC} = \dfrac{AP}{BP}$
$\dfrac{1}{2} = \dfrac{AP}{BP}$
$AP : BP = 1 : 2$
Perhatikan segitiga OAB, dan ingat perbandingan ruas garis dan vektor !
$\overrightarrow{OP} = \dfrac{2\overrightarrow{OA} + \overrightarrow{OB}}{2 + 1 }$
$\overrightarrow{OP} = \dfrac{2\overrightarrow{a} + \overrightarrow{b}}{3}$
$\overrightarrow{OP} = \dfrac{2}{3}\overrightarrow{a} + \dfrac{1}{3}\overrightarrow{b}$ → C.
$10$. Bentuk sederhana dari $3\overrightarrow{a} - (2\overrightarrow{b} + 5\overrightarrow{c}) - (2\overrightarrow{a} - \overrightarrow{b} +\overrightarrow{c})$ adalah . . . .
$A.\ \overrightarrow{a} + \overrightarrow{b} + 6\overrightarrow{c}$
$B.\ \overrightarrow{a} - \overrightarrow{b} - 6\overrightarrow{c}$
$C.\ 6\overrightarrow{a} + \overrightarrow{b} - \overrightarrow{c}$
$D.\ \overrightarrow{a} - 6\overrightarrow{b} + \overrightarrow{c}$
$E.\ \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$
$A.\ \overrightarrow{a} + \overrightarrow{b} + 6\overrightarrow{c}$
$B.\ \overrightarrow{a} - \overrightarrow{b} - 6\overrightarrow{c}$
$C.\ 6\overrightarrow{a} + \overrightarrow{b} - \overrightarrow{c}$
$D.\ \overrightarrow{a} - 6\overrightarrow{b} + \overrightarrow{c}$
$E.\ \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$
$3\overrightarrow{a} - (2\overrightarrow{b} + 5\overrightarrow{c}) - (2\overrightarrow{a} - \overrightarrow{b} +\overrightarrow{c})$
= $3\overrightarrow{a} - 2\overrightarrow{b} - 5\overrightarrow{c} - 2\overrightarrow{a} +\overrightarrow{b} - \overrightarrow{c}$
= $\overrightarrow{a} - \overrightarrow{b} - 6\overrightarrow{c}$ → B.
= $3\overrightarrow{a} - 2\overrightarrow{b} - 5\overrightarrow{c} - 2\overrightarrow{a} +\overrightarrow{b} - \overrightarrow{c}$
= $\overrightarrow{a} - \overrightarrow{b} - 6\overrightarrow{c}$ → B.
$11$. $\overrightarrow{a} = -\hat{i} + 4\hat{j}$, $\overrightarrow{b} = 2\hat{i} + \hat{j}$, $\overrightarrow{c} = 3\hat{i} - 4\hat{j}$, dan
$\overrightarrow{x} = p\overrightarrow{a} + q\overrightarrow{b}$ dengan p dan q bilangan real tidak nol. Jika $\overrightarrow{x}$ sejajar $\overrightarrow{c}$, maka p dan q memenuhi hubungan . . . .
$A.\ 8p - 11q = 0$.
$B.\ 8p + 11q = 0$
$C.\ 8p - 11q = 0$
$D.\ 11p - 8q = 0$
$E.\ 11p + 8q = 0$
[Soal UMPTN]
$\overrightarrow{x} = p\overrightarrow{a} + q\overrightarrow{b}$ dengan p dan q bilangan real tidak nol. Jika $\overrightarrow{x}$ sejajar $\overrightarrow{c}$, maka p dan q memenuhi hubungan . . . .
$A.\ 8p - 11q = 0$.
$B.\ 8p + 11q = 0$
$C.\ 8p - 11q = 0$
$D.\ 11p - 8q = 0$
$E.\ 11p + 8q = 0$
[Soal UMPTN]
$\overrightarrow{x} = p\overrightarrow{a} + q\overrightarrow{b}$
$\overrightarrow{x} = p(-\hat{i} + 4\hat{j}) + q(2\hat{i} + \hat{j})$
= $-p\hat{i} + 4p\hat{j} + 2q\hat{i} + q\hat{j}$
= $(2q - p)\hat{i} + (4p + q)\hat{j}$
$\overrightarrow{x}\ sejajar\ \overrightarrow{c}$
$\dfrac{2q - p}{3} = \dfrac{4p + q}{-4}$
$4p - 8q = 12p + 3q$
$8p + 11q = 0$ → B.
$\overrightarrow{x} = p(-\hat{i} + 4\hat{j}) + q(2\hat{i} + \hat{j})$
= $-p\hat{i} + 4p\hat{j} + 2q\hat{i} + q\hat{j}$
= $(2q - p)\hat{i} + (4p + q)\hat{j}$
$\overrightarrow{x}\ sejajar\ \overrightarrow{c}$
$\dfrac{2q - p}{3} = \dfrac{4p + q}{-4}$
$4p - 8q = 12p + 3q$
$8p + 11q = 0$ → B.
$12$. Diketahui $\overrightarrow{a} = 3\hat{i} - 2\hat{j}$, $\overrightarrow{b} = -\hat{i} + 4\hat{j}$, dan $\overrightarrow{r} = 7\hat{i} - 8\hat{j}$. Jika $\overrightarrow{r} = k\overrightarrow{a} + m\overrightarrow{b}$, maka $k + m =$ . . . .
$A.\ 3$
$B.\ 2$
$C.\ 1$
$D.\ -1$
$E.\ -2$
[Soal UMPTN]
$A.\ 3$
$B.\ 2$
$C.\ 1$
$D.\ -1$
$E.\ -2$
[Soal UMPTN]
$\overrightarrow{r} = k\overrightarrow{a} + m\overrightarrow{b}$
$7\hat{i} - 8\hat{j} = k(3\hat{i} - 2\hat{j}) + m(-\hat{i} + 4\hat{j})$
$7\hat{i} - 8\hat{j} = (3k - m)\hat{i} + (4m - 2k)\hat{j}$
Didapat dua persamaan dengan dua variabel.
$3k - m = 7$
$m = 3k - 7$ . . . . (1)
$4m - 2k = -8$ . . . . (2)
Substitusi (1) ke dalam (2)
$4(3k - 7) - 2k = -8$
$12k - 28 - 2k = -8$
$10k = 20$
$k = 2$.
$m = 3k - 7$ dari pers (1)
$m = 3.2 - 7$
$m = -1$
$k + m = 2 - 1$
$= 1.$ → C.
$7\hat{i} - 8\hat{j} = k(3\hat{i} - 2\hat{j}) + m(-\hat{i} + 4\hat{j})$
$7\hat{i} - 8\hat{j} = (3k - m)\hat{i} + (4m - 2k)\hat{j}$
Didapat dua persamaan dengan dua variabel.
$3k - m = 7$
$m = 3k - 7$ . . . . (1)
$4m - 2k = -8$ . . . . (2)
Substitusi (1) ke dalam (2)
$4(3k - 7) - 2k = -8$
$12k - 28 - 2k = -8$
$10k = 20$
$k = 2$.
$m = 3k - 7$ dari pers (1)
$m = 3.2 - 7$
$m = -1$
$k + m = 2 - 1$
$= 1.$ → C.
$13$. Jika vektor $\overrightarrow{a}$ dan vektor $\overrightarrow{b}$ membentuk sudut $60^{\circ}$, $|\overrightarrow{a}| = 4$ dan $|\overrightarrow{b}| = 3$, maka $\overrightarrow{a}.(\overrightarrow{a} - \overrightarrow{b})$ = . . . .
$A.\ 2$
$B.\ 4$
$C.\ 6$
$D.\ 8$
$E.\ 10$
$A.\ 2$
$B.\ 4$
$C.\ 6$
$D.\ 8$
$E.\ 10$
$\overrightarrow{a}.(\overrightarrow{a} - \overrightarrow{b}) = \overrightarrow{a}.\overrightarrow{a} - \overrightarrow{a}.\overrightarrow{b}$
$= |\overrightarrow{a}|^2 - |\overrightarrow{a}|.|\overrightarrow{b}|cos \theta$
$= 4^2 - 4.3.cos 60^{\circ}$
$= 4^2 - 4.3.\dfrac12$
$= 16 - 6$
$= 10$ → E.
Ingat !
$\overrightarrow{a}.\overrightarrow{a} = |\overrightarrow{a}|^2$
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos \theta$
$= |\overrightarrow{a}|^2 - |\overrightarrow{a}|.|\overrightarrow{b}|cos \theta$
$= 4^2 - 4.3.cos 60^{\circ}$
$= 4^2 - 4.3.\dfrac12$
$= 16 - 6$
$= 10$ → E.
Ingat !
$\overrightarrow{a}.\overrightarrow{a} = |\overrightarrow{a}|^2$
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos \theta$
$14$. Jika vektor $\overrightarrow{a} = \begin{pmatrix} 1\\ 2\\ 3\end{pmatrix}$, vektor $\overrightarrow{b} = \begin{pmatrix} 1\\ 0\\ 2\end{pmatrix}$, dan vektor $\overrightarrow{c} = \begin{pmatrix} 4\\ 2\\ 1\end{pmatrix}$
dengan $2\overrightarrow{a} + 3\overrightarrow{b} + k\overrightarrow{c} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$ dengan k bilangan
real. Maka nilai k = . . . .
$A.\ -1$
$B.\ -2$
$C.\ -3$
$D.\ 3$
$E.\ 2$
dengan $2\overrightarrow{a} + 3\overrightarrow{b} + k\overrightarrow{c} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$ dengan k bilangan
real. Maka nilai k = . . . .
$A.\ -1$
$B.\ -2$
$C.\ -3$
$D.\ 3$
$E.\ 2$
$2\overrightarrow{a} + 3\overrightarrow{b} + k\overrightarrow{c} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$
$2\begin{pmatrix} 1\\ 2\\ 3\end{pmatrix} + 3\begin{pmatrix} 1\\ 0\\ 2\end{pmatrix} + k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$
$\begin{pmatrix} 2\\ 4\\ 6\end{pmatrix} + \begin{pmatrix} 3\\ 0\\ 6\end{pmatrix} + k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$
$k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -8\\ -4\\ -2\end{pmatrix}$
$k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = -2\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix}$
$k = -2$ → B.
$2\begin{pmatrix} 1\\ 2\\ 3\end{pmatrix} + 3\begin{pmatrix} 1\\ 0\\ 2\end{pmatrix} + k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$
$\begin{pmatrix} 2\\ 4\\ 6\end{pmatrix} + \begin{pmatrix} 3\\ 0\\ 6\end{pmatrix} + k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -3\\ 0\\ 10\end{pmatrix}$
$k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = \begin{pmatrix} -8\\ -4\\ -2\end{pmatrix}$
$k\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix} = -2\begin{pmatrix} 4\\ 2\\ 1\end{pmatrix}$
$k = -2$ → B.
$15$. Diberikan vektor-vektor $\overrightarrow{a} = x\hat{i} - 3x\hat{j} + 6y\hat{k}$, $\overrightarrow{b} = (1 - y)\hat{i} + 3\hat{j} - (1 + x)\hat{k}$ dengan $x > 0$. Jika $\overrightarrow{a}$ dan $\overrightarrow{b}$ sejajar, maka $\overrightarrow{a} + 3\overrightarrow{b} =$ . . . .
$A.\ \overrightarrow{0}$
$B.\ -7\hat{i} + 21\hat{j} + 21\hat{k}$
$C.\ \hat{i} - 3\hat{j} - 3\hat{k}$
$D.\ 2\hat{i} + 3\hat{j} - 3\hat{k}$
$E.\ -6\hat{i} - 24\hat{k}$
[Soal SNMPTN]
$A.\ \overrightarrow{0}$
$B.\ -7\hat{i} + 21\hat{j} + 21\hat{k}$
$C.\ \hat{i} - 3\hat{j} - 3\hat{k}$
$D.\ 2\hat{i} + 3\hat{j} - 3\hat{k}$
$E.\ -6\hat{i} - 24\hat{k}$
[Soal SNMPTN]
Karena $\overrightarrow{a}$ sejajar $\overrightarrow{b}$, maka:
$\dfrac{x}{1 - y} = \dfrac{-3x}{3} = \dfrac{6y}{-(1 + x)}$
$\dfrac{x}{1 - y} = -x = \dfrac{6y}{-(1 + x)}$
Pertama:
$\dfrac{x}{1 - y} = -x$
$1 = y - 1$
$y = 2$
Kedua:
$-x = \dfrac{6y}{-(1 + x)}$
$x(1 + x) = 6y$
$x + x^2 = 6.2$
$x^2 + x - 12 = 0$
$(x + 4)(x - 3) = 0$
$x = -4\ atau\ x = 3$
Karena $x > 0$, maka $x$ yang memenuhi syarat adalah $x = 3$.
vektor-vektornya adalah:
$\overrightarrow{a} = 3\hat{i} - 9\hat{j} + 12\hat{k}$
$\overrightarrow{b} = -\hat{i} + 3\hat{j} - 4\hat{k}$
$\overrightarrow{a} + 3\overrightarrow{b} = \overrightarrow{0}$ → A.
$\dfrac{x}{1 - y} = \dfrac{-3x}{3} = \dfrac{6y}{-(1 + x)}$
$\dfrac{x}{1 - y} = -x = \dfrac{6y}{-(1 + x)}$
Pertama:
$\dfrac{x}{1 - y} = -x$
$1 = y - 1$
$y = 2$
Kedua:
$-x = \dfrac{6y}{-(1 + x)}$
$x(1 + x) = 6y$
$x + x^2 = 6.2$
$x^2 + x - 12 = 0$
$(x + 4)(x - 3) = 0$
$x = -4\ atau\ x = 3$
Karena $x > 0$, maka $x$ yang memenuhi syarat adalah $x = 3$.
vektor-vektornya adalah:
$\overrightarrow{a} = 3\hat{i} - 9\hat{j} + 12\hat{k}$
$\overrightarrow{b} = -\hat{i} + 3\hat{j} - 4\hat{k}$
$\overrightarrow{a} + 3\overrightarrow{b} = \overrightarrow{0}$ → A.
$16$. Vektor $\overrightarrow{u} = (x, y, 1)$ sejajar $\overrightarrow{v} = (-1, 3, z)$. Jika
$\overrightarrow{u}$ tegak lurus (3, -2, 3), maka y = . . . .
$A.\ 3$
$B.\ 1$
$C.\ \dfrac{1}{3}$
$D.\ -\dfrac{1}{3}$
$E.\ -1$
[UM UGM]
$\overrightarrow{u}$ tegak lurus (3, -2, 3), maka y = . . . .
$A.\ 3$
$B.\ 1$
$C.\ \dfrac{1}{3}$
$D.\ -\dfrac{1}{3}$
$E.\ -1$
[UM UGM]
Karena Vektor $\overrightarrow{u}$ sejajar $\overrightarrow{v}$ dan $\overrightarrow{u}$ tegak lurus $(3, -2, 3)$ maka $\overrightarrow{v}$ juga tegak lurus $(3, -2, 3)$.
Pertama:
$\overrightarrow{v}$ juga tegak lurus $(3, -2, 3)$.
$(-1, 3, z).(3, -2, 3) = 0$
$-3 - 6 + 3z = 0$
$3z = 9$
$z = 3$
Kedua:
$\overrightarrow{u}$ sejajar $\overrightarrow{v}$
$\dfrac{x}{-1} = \dfrac{y}{3} = \dfrac{1}{z}$
$\dfrac{x}{-1} = \dfrac{y}{3} = \dfrac{1}{3}$
$\dfrac{y}{3} = \dfrac{1}{3}$
$y = 1$ → B.
Pertama:
$\overrightarrow{v}$ juga tegak lurus $(3, -2, 3)$.
$(-1, 3, z).(3, -2, 3) = 0$
$-3 - 6 + 3z = 0$
$3z = 9$
$z = 3$
Kedua:
$\overrightarrow{u}$ sejajar $\overrightarrow{v}$
$\dfrac{x}{-1} = \dfrac{y}{3} = \dfrac{1}{z}$
$\dfrac{x}{-1} = \dfrac{y}{3} = \dfrac{1}{3}$
$\dfrac{y}{3} = \dfrac{1}{3}$
$y = 1$ → B.
$17$. Agar kedua vektor $\overrightarrow{a} = (x, 4, 7)$ dan $\overrightarrow{b} = (6, y, 14)$ segaris, haruslah nilai $x - y$ sama dengan . . . .
$A.\ -5$
$B.\ -2$
$C.\ 3$
$D.\ 4$
$E.\ 6$
[Soal UMPTN]
$A.\ -5$
$B.\ -2$
$C.\ 3$
$D.\ 4$
$E.\ 6$
[Soal UMPTN]
vektor $\overrightarrow{a}$ koliner dengan vektor $\overrightarrow{b}$, sehingga:
$vektor\ \overrightarrow{a} = k.vektor\ \overrightarrow{b}$
$(x, 4, 7) = k(6, y, 14)$
$(x, 4, 7) = (6k, ky, 14k)$
$7 = 14k → k = \dfrac{1}{2}$
$x = 6k$
$= 6.\dfrac{1}{2}$
$= 3$
$4 = ky$
$4 = \dfrac{1}{2}y$
$y = 8$
$x - y = 3 - 8$
$= -5$ → A.
$vektor\ \overrightarrow{a} = k.vektor\ \overrightarrow{b}$
$(x, 4, 7) = k(6, y, 14)$
$(x, 4, 7) = (6k, ky, 14k)$
$7 = 14k → k = \dfrac{1}{2}$
$x = 6k$
$= 6.\dfrac{1}{2}$
$= 3$
$4 = ky$
$4 = \dfrac{1}{2}y$
$y = 8$
$x - y = 3 - 8$
$= -5$ → A.
$18.\ A = (-1, 5, 4)$; $B = (2, -1, -2)$; $C = (3, p, q)$. Jika titik-titik $A,\ B,\ dan\ C$ segaris, maka nilai $p\ dan\ q$ berturut-turut adalah . . . .
$A.\ -3\ dan\ -4$
$B.\ -1\ dan| -4$
$C.\ -3\ dan\ 0$
$D.\ -1\ dan\ 0$
$E.\ 3\ dan\ 0$
[Soal UMPTN]
$A.\ -3\ dan\ -4$
$B.\ -1\ dan| -4$
$C.\ -3\ dan\ 0$
$D.\ -1\ dan\ 0$
$E.\ 3\ dan\ 0$
[Soal UMPTN]
$\overrightarrow{AB} = \overrightarrow{b} - \overrightarrow{a}$
$= (3, -6, -6)$
$\overrightarrow{BC} = \overrightarrow{c} - \overrightarrow{b}$
$= (1, p + 1, q + 2)$
$\overrightarrow{AB}$ segaris atau koliner dengan $\overrightarrow{BC}$
$\overrightarrow{AB} = k\overrightarrow{BC}$
$(3, -6, -6) = k(1, p + 1, q + 2)$
$(3, -6, -6) = (k, k(p + 1), k(q + 2))$
$k = 3$
$k(p + 1) = -6$
$3(p + 1) = -6$
$3p + 3 = -6$
$3p = -9$
$p = -3$
$k(q + 2) = -6$
$3(q + 2) = -6$
$3q + 6 = -6$
$3q = -12$
$q = -4$
$Jadi\ p = -3,\ q = -4$ → A.
$= (3, -6, -6)$
$\overrightarrow{BC} = \overrightarrow{c} - \overrightarrow{b}$
$= (1, p + 1, q + 2)$
$\overrightarrow{AB}$ segaris atau koliner dengan $\overrightarrow{BC}$
$\overrightarrow{AB} = k\overrightarrow{BC}$
$(3, -6, -6) = k(1, p + 1, q + 2)$
$(3, -6, -6) = (k, k(p + 1), k(q + 2))$
$k = 3$
$k(p + 1) = -6$
$3(p + 1) = -6$
$3p + 3 = -6$
$3p = -9$
$p = -3$
$k(q + 2) = -6$
$3(q + 2) = -6$
$3q + 6 = -6$
$3q = -12$
$q = -4$
$Jadi\ p = -3,\ q = -4$ → A.
$19$. Diketahui $\overrightarrow{a} + \overrightarrow{b} = \hat{i} - \hat{j} + 4\hat{k}$ dan $|\overrightarrow{a} - \overrightarrow{b}| = \sqrt{14}$. Hasil dari $\overrightarrow{a}.\overrightarrow{b} =$ . . . .
$A.\ 4$
$B.\ 2$
$C.\ 1$
$D.\ \dfrac{1}{2}$
$E.\ 0$
[Soal SPMB]
$A.\ 4$
$B.\ 2$
$C.\ 1$
$D.\ \dfrac{1}{2}$
$E.\ 0$
[Soal SPMB]
Dari:
$\overrightarrow{a} + \overrightarrow{b} = \hat{i} - \hat{j} + 4\hat{k}$
Didapat:
$|\overrightarrow{a} + \overrightarrow{b}|^2 = 1^2 + (-1)^2 + 4^2$
$|\overrightarrow{a} + \overrightarrow{b}|^2 = 18$
Ingat !
$\bullet$ $|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta$
sehingga:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 18$ . . . . (1)
Karena:
$|\overrightarrow{a} - \overrightarrow{b}| = \sqrt{14}$.
maka:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 14$ . . . . (2)
Eliminasi persamaan (1) dan (2)
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 18$ . . . . (1)
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 14$ . . . . (2)
---------------------------------------------------------------- ---
$4|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 4$
$|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 1$
Ingat !
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos \theta$
$\overrightarrow{a}.\overrightarrow{b} = 1$ → C.
$\overrightarrow{a} + \overrightarrow{b} = \hat{i} - \hat{j} + 4\hat{k}$
Didapat:
$|\overrightarrow{a} + \overrightarrow{b}|^2 = 1^2 + (-1)^2 + 4^2$
$|\overrightarrow{a} + \overrightarrow{b}|^2 = 18$
Ingat !
$\bullet$ $|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta$
sehingga:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 18$ . . . . (1)
Karena:
$|\overrightarrow{a} - \overrightarrow{b}| = \sqrt{14}$.
maka:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 14$ . . . . (2)
Eliminasi persamaan (1) dan (2)
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 18$ . . . . (1)
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 14$ . . . . (2)
---------------------------------------------------------------- ---
$4|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 4$
$|\overrightarrow{a}||\overrightarrow{b}|cos \theta = 1$
Ingat !
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos \theta$
$\overrightarrow{a}.\overrightarrow{b} = 1$ → C.
$20$. Diberikan vektor $\overrightarrow{a}$ dan $\overrightarrow{b}$. Jika $|\overrightarrow{a} + \overrightarrow{b}|^2 = \overrightarrow{a}.\overrightarrow{b}$ dan $(|\overrightarrow{a}| + |\overrightarrow{b}|)^2 = \dfrac{5}{ 2}|\overrightarrow{a}|.|\overrightarrow{b}|$, maka sudut antara vektor $\overrightarrow{a}$ dan $\overrightarrow{b}$ adalah . . . .
$A.\ 30^o$
$B.\ 45^o$
$C.\ 60^o$
$D.\ 90^o$
$E.\ 120^o$
[Soal SBMPTN]
$A.\ 30^o$
$B.\ 45^o$
$C.\ 60^o$
$D.\ 90^o$
$E.\ 120^o$
[Soal SBMPTN]
Ingat !
$\bullet$ $|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
$\bullet$ $\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
sehingga:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta = |\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 = -|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$ . . . . (1)
Dari:
$(|\overrightarrow{a}| + |\overrightarrow{b}|)^2 = \dfrac{5}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
Didapat:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}|.|\overrightarrow{b}| = \dfrac{5}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 = \dfrac{1}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$ . . . . (2)
Substitusi persamaan (1) ke dalam persamaan (2)
$-|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta = \dfrac{1}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
$-cos\ \theta = \dfrac{1}{2}$
$cos\ \theta = -\dfrac{1}{2}$
$\theta = 120^o$ → E.
$\bullet$ $|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
$\bullet$ $\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
sehingga:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta = |\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 = -|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta$ . . . . (1)
Dari:
$(|\overrightarrow{a}| + |\overrightarrow{b}|)^2 = \dfrac{5}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
Didapat:
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2|\overrightarrow{a}|.|\overrightarrow{b}| = \dfrac{5}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
$|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 = \dfrac{1}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$ . . . . (2)
Substitusi persamaan (1) ke dalam persamaan (2)
$-|\overrightarrow{a}||\overrightarrow{b}|cos\ \theta = \dfrac{1}{2}|\overrightarrow{a}|.|\overrightarrow{b}|$
$-cos\ \theta = \dfrac{1}{2}$
$cos\ \theta = -\dfrac{1}{2}$
$\theta = 120^o$ → E.
$21$. Diketahui vektor $\overrightarrow{a} = 4\hat{i} - 2\hat{j} + 2\hat{k}$ dan vektor
$\overrightarrow{b} = 2\hat{i} - 6\hat{j} + 4\hat{k}$. Proyeksi vektor orthogonal vektor $\overrightarrow{a}$
terhadap vektor $\overrightarrow{b}$ adalah . . . .
$A.\ \hat{i} - \hat{j} + \hat{k}$
$B.\ \hat{i} - 3\hat{j} + 2\hat{k}$
$C.\ \hat{i} - 4\hat{j} + 4\hat{k}$
$D.\ 2\hat{i} - \hat{j} + \hat{k}$
$E.\ 6\hat{i} - 8\hat{j} + 6\hat{k}$
[Soal UN]
$\overrightarrow{b} = 2\hat{i} - 6\hat{j} + 4\hat{k}$. Proyeksi vektor orthogonal vektor $\overrightarrow{a}$
terhadap vektor $\overrightarrow{b}$ adalah . . . .
$A.\ \hat{i} - \hat{j} + \hat{k}$
$B.\ \hat{i} - 3\hat{j} + 2\hat{k}$
$C.\ \hat{i} - 4\hat{j} + 4\hat{k}$
$D.\ 2\hat{i} - \hat{j} + \hat{k}$
$E.\ 6\hat{i} - 8\hat{j} + 6\hat{k}$
[Soal UN]
Ingat !
Jika proyeksi vektor orthogonal vektor $\overrightarrow{a}$ terhadap vektor $\overrightarrow{b}$ adalah $\overrightarrow{c}$,
maka:
$\overrightarrow{c} = \dfrac{\overrightarrow{a}.\overrightarrow{b}}{ |\overrightarrow{b}|^2}.\overrightarrow{b}$
$\overrightarrow{c} = \dfrac{(4, -2, 2).(2, -6, 4)}{(2^2 + (-6)^2 + 4^2)}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = \dfrac{28}{56}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = \dfrac{1}{2}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = (\hat{i} - 3\hat{j} + 2\hat{k})$ → B.
Jika proyeksi vektor orthogonal vektor $\overrightarrow{a}$ terhadap vektor $\overrightarrow{b}$ adalah $\overrightarrow{c}$,
maka:
$\overrightarrow{c} = \dfrac{\overrightarrow{a}.\overrightarrow{b}}{ |\overrightarrow{b}|^2}.\overrightarrow{b}$
$\overrightarrow{c} = \dfrac{(4, -2, 2).(2, -6, 4)}{(2^2 + (-6)^2 + 4^2)}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = \dfrac{28}{56}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = \dfrac{1}{2}.(2\hat{i} - 6\hat{j} + 4\hat{k})$
$\overrightarrow{c} = (\hat{i} - 3\hat{j} + 2\hat{k})$ → B.
$22$. Agar vektor $\overrightarrow{a} = 2\hat{i} + p\hat{j} + \hat{k}$ dan $\overrightarrow{b} = 3\hat{i} + 2\hat{j} + 4\hat{k}$ saling tegak lurus, maka nilai $p$ adalah . . . .
$A.\ 5$
$B.\ -5$
$C.\ -8$
$D.\ -9$
$E.\ -10$
[Soal SNMPTN]
$A.\ 5$
$B.\ -5$
$C.\ -8$
$D.\ -9$
$E.\ -10$
[Soal SNMPTN]
Vektor $\overrightarrow{a}$ dan vektor $\overrightarrow{b}$ saling tegak lurus jika sudut antara kedua vektor adalah $90^o$.
Ingat perkalian vektor.
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos\ \theta$
$(2, p, 1)(3, 2, 4) = 0$ → $cos\ 90^o = 0$
$6 + 2p + 4 = 0$
$2p + 10 = 0$
$p = -5$ → B.
Ingat perkalian vektor.
$\overrightarrow{a}.\overrightarrow{b} = |\overrightarrow{a}|.|\overrightarrow{b}|cos\ \theta$
$(2, p, 1)(3, 2, 4) = 0$ → $cos\ 90^o = 0$
$6 + 2p + 4 = 0$
$2p + 10 = 0$
$p = -5$ → B.
$23$. Diketahui vektor $\overrightarrow{a} = \begin{pmatrix} p\\ 2\\ -1\end{pmatrix}$; $\overrightarrow{b} = \begin{pmatrix} 4\\ -3\\ 6\end{pmatrix}$; $\overrightarrow{c} = \begin{pmatrix} 2\\ -1\\ 3\end{pmatrix}$. Jika $\overrightarrow{a}$ tegak lurus $\overrightarrow{b}$, maka hasil dari $(\overrightarrow{a} - 2\overrightarrow{b}).3\overrightarrow{c}$ adalah . . . .
$A.\ 171$
$B.\ 63$
$C.\ -63$
$D.\ -111$
$E.\ -171$
[Soal UN]
$A.\ 171$
$B.\ 63$
$C.\ -63$
$D.\ -111$
$E.\ -171$
[Soal UN]
Karena $\overrightarrow{a}$ tegak lurus $\overrightarrow{b}$, maka: $\overrightarrow{a}.\overrightarrow{b} = 0$
$(p, 2, -1).(4, -3, 6) = 0$
$4p - 6 - 6 = 0$
$4p = 12$
$p = 3$
$\left(\overrightarrow{a} - 2\overrightarrow{b}\right).3\overrightarrow{c}$
$= \left(\begin{pmatrix} 3\\ 2\\ -1\end{pmatrix} - 2\begin{pmatrix} 4\\ -3\\ 6\end{pmatrix}\right).3\begin{pmatrix} 2\\ -1\\ 3\end{pmatrix}$
$= \left(\begin{pmatrix} 3\\ 2\\ -1\end{pmatrix} - \begin{pmatrix} 8\\ -6\\ 12\end{pmatrix}\right).\begin{pmatrix} 6\\ -3\\ 9\end{pmatrix}$
$= \begin{pmatrix} -5\\ 8\\ -13\end{pmatrix}.\begin{pmatrix} 6\\ -3\\ 9\end{pmatrix}$
$= -30 - 24 - 117$
$= -171$ → E.
$(p, 2, -1).(4, -3, 6) = 0$
$4p - 6 - 6 = 0$
$4p = 12$
$p = 3$
$\left(\overrightarrow{a} - 2\overrightarrow{b}\right).3\overrightarrow{c}$
$= \left(\begin{pmatrix} 3\\ 2\\ -1\end{pmatrix} - 2\begin{pmatrix} 4\\ -3\\ 6\end{pmatrix}\right).3\begin{pmatrix} 2\\ -1\\ 3\end{pmatrix}$
$= \left(\begin{pmatrix} 3\\ 2\\ -1\end{pmatrix} - \begin{pmatrix} 8\\ -6\\ 12\end{pmatrix}\right).\begin{pmatrix} 6\\ -3\\ 9\end{pmatrix}$
$= \begin{pmatrix} -5\\ 8\\ -13\end{pmatrix}.\begin{pmatrix} 6\\ -3\\ 9\end{pmatrix}$
$= -30 - 24 - 117$
$= -171$ → E.
$24$. Jika $\overrightarrow{u}$ dan $\overrightarrow{v}$ adalah dua vektor satuan membentuk sudut $30^o$, maka $(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{v}$ = . . . .
$A.\ \dfrac{3}{2}$
$B.\ \dfrac{\sqrt{3}}{2} + 1$
$C.\ \dfrac{\sqrt{3}}{2} - 1$
$D.\ \dfrac{\sqrt{2}}{2} + 1$
$E.\ \dfrac{1}{\sqrt{3}} + 1$
[Soal SNMPTN]
$A.\ \dfrac{3}{2}$
$B.\ \dfrac{\sqrt{3}}{2} + 1$
$C.\ \dfrac{\sqrt{3}}{2} - 1$
$D.\ \dfrac{\sqrt{2}}{2} + 1$
$E.\ \dfrac{1}{\sqrt{3}} + 1$
[Soal SNMPTN]
Ingat !
Panjang dari vektor satuan = 1.
$(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{v} = \overrightarrow{u}.\overrightarrow{v} + \overrightarrow{v}.\overrightarrow{v}$
$= |\overrightarrow{u}|.|\overrightarrow{v}|cos \theta + |\overrightarrow{v}|^2$
$= 1.1.\dfrac{1}{2}\sqrt{3} + 1$
$= \dfrac{1}{2}\sqrt{3} + 1$ → B.
Panjang dari vektor satuan = 1.
$(\overrightarrow{u} + \overrightarrow{v}).\overrightarrow{v} = \overrightarrow{u}.\overrightarrow{v} + \overrightarrow{v}.\overrightarrow{v}$
$= |\overrightarrow{u}|.|\overrightarrow{v}|cos \theta + |\overrightarrow{v}|^2$
$= 1.1.\dfrac{1}{2}\sqrt{3} + 1$
$= \dfrac{1}{2}\sqrt{3} + 1$ → B.
$25$. Diketahui titik $A(1, -2, -8)$ dan titik $B(3, -4, 0)$. Titik $P$ terletak pada perpanjangan $AB$ sehingga $\overrightarrow{AP} = -3\overrightarrow{PB}$. Jika $\overrightarrow{p}$ merupakan vektor posisi titik $P$, maka $\overrightarrow{p} =$ . . . .
$A.\ 4\hat{i} - 5\hat{j} + 4\hat{k}$
$B.\ 4\hat{i} - 5\hat{j} - 4\hat{k}$
$C.\ -{j} - 12\hat{k}$
$D.\ -3\hat{i} - \hat{j} - 12\hat{k}$
$E.\ -\hat{i} - 5\hat{j} - 2\hat{k}$
[Soal SPMB]
$A.\ 4\hat{i} - 5\hat{j} + 4\hat{k}$
$B.\ 4\hat{i} - 5\hat{j} - 4\hat{k}$
$C.\ -{j} - 12\hat{k}$
$D.\ -3\hat{i} - \hat{j} - 12\hat{k}$
$E.\ -\hat{i} - 5\hat{j} - 2\hat{k}$
[Soal SPMB]
Misalkan titik $P(x, y, z)$
$\overrightarrow{AP} = -3\overrightarrow{PB}$
$\overrightarrow{AP} = 3\overrightarrow{BP}$
$\overrightarrow{p} - \overrightarrow{a} = 3(\overrightarrow{p} -\overrightarrow{b})$
$\begin{pmatrix} x\\ y\\ z\end{pmatrix} - \begin{pmatrix} 1\\ -2\\ -8\end{pmatrix} = 3\left(\begin{pmatrix} x\\ y\\ z\end{pmatrix} - \begin{pmatrix} 3\\ -4\\ 0\end{pmatrix}\right)$
$\begin{pmatrix} x - 1\\ y + 2\\ z + 8\end{pmatrix} = 3\begin{pmatrix} x - 3\\ y + 4\\ z\end{pmatrix}$
$z + 8 = 3z$
$z = 4$
$y + 2 = 3y + 12$
$-10 = 2y$
$y = -5$
$x - 1 = 3x - 9$
$2x = 8$
$x = 4$
Koordinat titik $P = (4, -5, 4)$, maka $\overrightarrow{p} = 4\hat{i} - 5\hat{j} + 4\hat{k}$ → A.
$\overrightarrow{AP} = -3\overrightarrow{PB}$
$\overrightarrow{AP} = 3\overrightarrow{BP}$
$\overrightarrow{p} - \overrightarrow{a} = 3(\overrightarrow{p} -\overrightarrow{b})$
$\begin{pmatrix} x\\ y\\ z\end{pmatrix} - \begin{pmatrix} 1\\ -2\\ -8\end{pmatrix} = 3\left(\begin{pmatrix} x\\ y\\ z\end{pmatrix} - \begin{pmatrix} 3\\ -4\\ 0\end{pmatrix}\right)$
$\begin{pmatrix} x - 1\\ y + 2\\ z + 8\end{pmatrix} = 3\begin{pmatrix} x - 3\\ y + 4\\ z\end{pmatrix}$
$z + 8 = 3z$
$z = 4$
$y + 2 = 3y + 12$
$-10 = 2y$
$y = -5$
$x - 1 = 3x - 9$
$2x = 8$
$x = 4$
Koordinat titik $P = (4, -5, 4)$, maka $\overrightarrow{p} = 4\hat{i} - 5\hat{j} + 4\hat{k}$ → A.
Demikianlah Soal dan Pembahasan Vektor. Selamat belajar !
www.maretong.com






bagus dan terimaksih
ReplyDeleteMantap sekali
ReplyDeleteTerimakasih
ReplyDeletemakasihhh:v
ReplyDeleteTerima kasih:)
ReplyDeletecontoh soal beragam, terimakasih!
ReplyDeleteTerimah kasih soalnya baru² semua aku bisa belajar bentuk yang baru agak kesulitan aku sih
ReplyDeleteno20 seharusnya akar lal^2+lbl^2+2lallblcos teta = lallblcos teta
ReplyDeletekarena di keterngnnya la+bl=a.b bukan la+bl^2=a.b
makasihh (✿^‿^)
ReplyDeletemohon ijin share
ReplyDeletemakasih modulnya bagus bgt ,boleh minta file yang bisa didowlodnya donk
ReplyDeletebagus makasih
ReplyDelete