Daftar isi
Soal dan Pembahasan Trigonometri SMA kelas 10. Trigonometri merupakan nilai perbandingan sisi-sisi pada segitiga siku-siku maupun koordinat Cartesius yang dikaitkan dengan suatu sudut. Ada enam perbandingan yang menjadi dasar dari trigonometri, yaitu sinus (sin), cosinus (cos), tangen (tan), sekan (sec), cosekan (csc), dan cotangen (cot).
Perbandingan Trigonometri
1. Perbandingan Trigonometri Dalam Segitiga Siku-Siku
Segitiga siku-siku terdiri dari dua sisi yang saling tegak lurus dan satu sisi miring. Trigonometri merupakan besar suatu sudut yang dinyatakan dalam bentuk perbandingan panjang sisi-sisi segitiga tersebut. Perhatikan gambar dan keterangan di bawah !$Sinus = \dfrac{Depan}{Miring}$ $\Rightarrow$ $sin \:\alpha = \dfrac{y}{r}$ || $cosec\:\alpha = \dfrac{r}{y}$
$Cosinus = \dfrac{Samping}{Miring}$ $\Rightarrow$ $cos\:\alpha = \dfrac{x}{r}$ || $sec\:\alpha = \dfrac{r}{x}$
$Tangen = \dfrac{Depan}{Samping}$ $\Rightarrow$ $tan\:\alpha = \dfrac{y}{x}$ || $cot\:\alpha = \dfrac{x}{y}$
2. Perbandingan Trigonometri Dalam Koordinat Cartesius
Trigonometri bukan hanya perbandingan sisi-sisi pada segitiga siku-siku. Perbandingan trigonometri juga dapat dinyatakan dalam koordinat Cartesius. Trigonometri dalam segitiga siku-siku terbatas hanya pada sudut lancip, sedangkan dalam koordinat Cartesius bisa mencakup sudut-sudut tumpul. Perhatikan gambar dan keterangan di bawah !$sinus = \dfrac{ordinat}{radius}$ $\Rightarrow$ $sin\:\alpha = \dfrac{b}{r}$ || $cosec\:\alpha = \dfrac{r}{b}$
$cosinus = \dfrac{absis}{radius}$ $\Rightarrow$ $cos\:\alpha = \dfrac{a}{r}$ || $sec\:\alpha = \dfrac{r}{a}$
$tangen = \dfrac{ordinat}{absis}$ $\Rightarrow$ $tan\:\alpha = \dfrac{b}{a}$ || $cot\:\alpha = \dfrac{a}{b}$
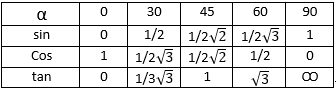
3. Sudut-sudut Istimewa
4. Pengertian Kuadran
Kuadran adalah empat bidang yang sama besar yang dibatasi oleh sistem koordinat Cartesius. Sudut $0^{\circ}$ adalah acuan perputaran yang arahnya berlawanan putaran jarum jam. Empat bidang yang terbentuk dibagi menjadi empat kuadran.$Kuadran\ I:\ 0^{\circ} < α < 90^{\circ}$
$Kuadran\ II:\ 90^{\circ} < α < 180^{\circ}$
$Kuadran\ III:\ 180^{\circ} < α < 270^{\circ}$
$Kuadran\ IV:\ 270^{\circ} < α < 3600^{\circ}$
Rumus Sudut-sudut Berelasi
$A.\: Relasi \;\theta\; dengan \;(90^{\circ} - \theta)$$sin\:(90^{\circ} - \theta) = cos\:\theta$ || $cosec\:(90^{\circ} - \theta) = sec \:\theta$
$cos\:(90^{\circ} - \theta) = sin\:\theta$ || $sec\:(90^{\circ} - \theta) = cosec\:\theta$
$tan\:(90^{\circ} - \theta) = cot\:\theta$ || $cot\:(90^{\circ} - \theta) = tan\:\theta$
$B.\: Relasi \;\theta\; dengan \;(90^{\circ} + \theta)$
$sin\:(90^{\circ} + \theta) = cos\:\theta$ || $cosec\:(90^{\circ} + \theta) = sec\:\theta$
$cos\:(90^{\circ} + \theta) = -sin\:\theta$ || $sec\:(90^{\circ} + \theta) = -cosec\:\theta$
$tan\:(90^{\circ} + \theta) = -cot\:\theta$ || $cot\:(90^{\circ} + \theta) = -tan\:\theta$
$C.\: Relasi\; \theta\; dengan \;(270^{\circ} - \theta)$
$sin\:(270^{\circ} - \theta) = -cos\:\theta$ || $cosec\:(270^{\circ} - \theta) = -sec\:\theta$
$cos\:(270^{\circ} - \theta) = -sin\:\theta$ || $sec\:(270^{\circ} - \theta) = -cosec\:\theta$
$tan\:(270^{\circ} - \theta) = cot\:\theta$ || $cot\:(270^{\circ} - \theta) = tan\:\theta$
$D.\: Relasi \;\theta\; dengan \;(270^{\circ} + \theta)$
$sin\:(270^{\circ} + \theta) = -cos\:\theta$ || $cosec\:(270^{\circ} + \theta) = -sec\:\theta$
$cos\:(270^{\circ} + \theta) = sin\:\theta$ || $sec\:(270^{\circ} + \theta) = cosec\:\theta$
$tan\:(270^{\circ} + \theta) = -cot\:\theta$ || $cot\:(270^{\circ} + \theta) = -tan\:\theta$
$E.\: Relasi\; \theta\; dengan \;(-\theta)$
$sin\:(-\theta) = -sin\:\theta$ || $cosec\:(-\theta) = -cosec\:\theta$
$cos\:(-\theta) = cos\:\theta$ || $sec\:(-\theta) = sec\:\theta$
$tan\:(-\theta) = -tan\:\theta$ || $cot\:(-\theta) = -cot\:\theta$
$F.\: Relasi\; \theta\; dengan \;(360^{\circ} + \theta)$
$sin \:(360^{\circ} + \theta) = sin \:\theta$ || $cosec \:(360^{\circ} + \theta) = cosec \:\theta$
$cos \:(360^{\circ} + \theta) = cos \:\theta$ || $sec \:(360^{\circ} + \theta) = sec \:\theta$
$tan \:(360^{\circ} + \theta) = tan \:\theta$ || $cot \:(360^{\circ} + \theta) = cot \:\theta$
$G.\: Relasi \;\theta\; dengan \;(180^{\circ} - \theta)$
$sin \:(180^{\circ} - \theta) = sin \:\theta$ || $cosec \:(180^{\circ} - \theta) = cosec \:\theta$
$cos \:(180^{\circ} - \theta) = -cos \:\theta$ || $sec \:(180^{\circ} - \theta) = -sec \:\theta$
$tan \:(180^{\circ} - \theta) = -tan \:\theta$ || $cot \:(180^{\circ} - \theta) = -cot \:\theta$
$H.\: Relasi \;\theta\; dengan \;(180^{\circ} + \theta)$
$sin \:(180^{\circ} + \theta) = -sin \:\theta$ || $cosec \:(180^{\circ} + \theta) = -cosec \:\theta$
$cos \:(180^{\circ} + \theta) = -cos \:\theta$ || $sec \:(180^{\circ} + \theta) = -sec \:\theta$
$tan \:(180^{\circ} + \theta) = tan \:\theta$ || $cot \:(180^{\circ} - \theta) = cot \:\theta$
$I.\: Relasi \;\theta\; dengan \;(360^{\circ} - \theta)$
$sin \:(360^{\circ} - \theta) = -sin \:\theta$ || $cosec \:(360^{\circ} - \theta) = -cosec \:\theta$
$cos \:(360^{\circ} - \theta) = cos \:\theta$ || $sec \:(360^{\circ} - \theta) = sec \:\theta$
$tan \:(360^{\circ} - \theta) = -tan \:\theta$ || $cot \:(360^{\circ} - \theta) = -cot \:\theta$
Koordinat Kutub dan Koordinat Cartesius
Terdapat hubungan antara koordinat kutub dengan koordinat cartesius. $P(a, b)$ disebut koordinat cartesius dan $P(r,\; \alpha)$ disebut sebagai koordinat kutub. Dalam hal ini berlaku hubungan sebagai berikut:
$Sin\ \alpha = \dfrac{b}{r} → b = r sin \:\alpha$
$Cos\ \alpha = \dfrac{a}{r} → a = r cos \:\alpha$
$tan\ \alpha = \dfrac{b}{a} → \alpha = arc\:\left[tan \:\left(\dfrac{b}{a}\right)\right]$
$r = \sqrt{a^{2} + b^{2}}$
Rumus Identitas Trigonometri
$1.\: sec \:\theta = \dfrac{1}{cos\: θ}$$2.\: cosec\: \theta = \dfrac{1}{sin\: θ}$
$3.\: cot\:\theta = \dfrac{1}{tan\:\theta}$
$4.\: tan\:\theta = \dfrac{sin\:\theta}{cos\:\theta}$
$5.\: cot\:\theta = \dfrac{cos\:\theta}{sin\:\theta}$
$6.\: sin^{2}\:\theta + cos^{2}\:\theta = 1$
$7.\: 1 + tan^{2}\:\theta = sec^{2}\:\theta$
$8.\: 1 + cot^{2}\:\theta = cosec^{2}\:\theta$
Aturan Sinus dan Cosinus
1. Rumus Aturan Sinus
$\dfrac{a}{sin A} = \dfrac{b}{sin B} = \dfrac{c}{sin C}$2. Rumus Aturan Cosinus
$1.\: a^{2} = b^{2} + c^{2} - 2bcCos\; A$$2.\: b^{2} = a^{2} + c^{2} - 2acCos\; B$
$3.\: c^{2} = a^{2} + b^{2} - 2abCos\: C$
3. Rumus Luas Segitiga Sembarang
$L = \dfrac{1}{2}abSin\; C$$L = \dfrac{1}{2}acSin\; B$
$L = \dfrac{1}{2}bcSin\; A$
$L = \dfrac{a^{2}Sin\; B Sin\; C}{2Sin\; (B + C)}$
$L = \dfrac{b^{2}Sin\; A Sin\; C}{2Sin\; (A + C)}$
$L = \dfrac{c^{2}Sin\; A Sin\; B}{2Sin\; (A + B)}$
$L = \sqrt{s(s - a)(s - b)(s - c)}$ dengan $s = \dfrac{1}{2}(a + b + c)$
4. Rumus Luas Segi n Beraturan
A. Jika jari-jari lingkaran luar segi $n$ diketahui adalah $R$ maka luas $(L)$ segi $n$ beraturan adalah:
$L = \dfrac{n}{2}R^{2}sin\;\left(\dfrac{360}{n}\right)$
B. Jika panjang sisi segi $n$ beraturan diketahui adalah $p$ maka luas segi $n$ beraturan adalah:
$L = \dfrac{n}{4}p^{2}cot\;\left(\dfrac{180}{n}\right)$
Contoh Soal Trigonometri SMA kelas 10 dan Pembahasan
$1$. Perhatikan segitiga ABC dibawah! Segitiga ABC siku-siku di B.
Maka $sin \;\theta =$ . . . .
$A.\ \dfrac ab$
$B.\ \dfrac ac$
$C.\ \dfrac ca$
$D.\ \dfrac cb$
$E.\ \dfrac ba$
Maka $sin \;\theta =$ . . . .
$A.\ \dfrac ab$
$B.\ \dfrac ac$
$C.\ \dfrac ca$
$D.\ \dfrac cb$
$E.\ \dfrac ba$
$sin \;θ = \dfrac{c}{b}$
ingat !
$sin = \dfrac{depan}{miring}$ → D.
ingat !
$sin = \dfrac{depan}{miring}$ → D.
$2$. Segitiga PQR siku-siku di R. $2cos\; \alpha - sin\; \beta$ = . . . .
$A.\ \dfrac 35$
$B.\ \dfrac 45$
$C.\ 1$
$D.\ \dfrac 53$
$E.\ \dfrac 54$
$A.\ \dfrac 35$
$B.\ \dfrac 45$
$C.\ 1$
$D.\ \dfrac 53$
$E.\ \dfrac 54$
$PQ = 5$ → dalil phytagoras.
$cos\; α = \dfrac{PR}{PQ} = \dfrac{4}{5}$
$sin\; β = \dfrac{PR}{PQ} = \dfrac{4}{5}$
$2cos\; α - sin\; β = 2.\dfrac{4}{5} - \dfrac{4}{5}$
$= \dfrac{4}{5}$ → B.
$cos\; α = \dfrac{PR}{PQ} = \dfrac{4}{5}$
$sin\; β = \dfrac{PR}{PQ} = \dfrac{4}{5}$
$2cos\; α - sin\; β = 2.\dfrac{4}{5} - \dfrac{4}{5}$
$= \dfrac{4}{5}$ → B.
$3$. Jika $sin\ α = \dfrac {5}{13}$, dengan $α$ sudut lancip, maka $cos\ α =$ . . . .
$A.\ \dfrac{5}{12}$
$B.\ 1$
$C.\ \dfrac{13}{12}$
$D.\ \dfrac{12}{5}$
$E.\ \dfrac{12}{13}$
$A.\ \dfrac{5}{12}$
$B.\ 1$
$C.\ \dfrac{13}{12}$
$D.\ \dfrac{12}{5}$
$E.\ \dfrac{12}{13}$
$4.$ Jika $tan\ A = \dfrac34$, dengan $A$ sudut lancip. Maka $2sin\ A + cos\ A =$ . . . .
$A.\ 1$
$B.\ \dfrac32$
$C.\ 2$
$D.\ 3$
$E.\ 4$
$A.\ 1$
$B.\ \dfrac32$
$C.\ 2$
$D.\ 3$
$E.\ 4$
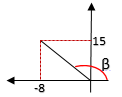
$5.$ Perhatikan gambar dibawah! Nilai $sin\ β$ adalah . . . .
$A.\ -\dfrac{15}{17}$
$B.\ \dfrac{15}{17}$
$C.\ -\dfrac{8}{17}$
$D.\ \dfrac{8}{17}$
$E.\ -\dfrac{8}{15}$
$A.\ -\dfrac{15}{17}$
$B.\ \dfrac{15}{17}$
$C.\ -\dfrac{8}{17}$
$D.\ \dfrac{8}{17}$
$E.\ -\dfrac{8}{15}$
$x = -8,\ y = 15,\ r = 17$ → Phytagoras
Koordinat Cartesius → $sin = \dfrac{ordinat}{radius}$
$sin\; β = \dfrac{y}{r} = \dfrac{15}{17}$ → B.
Koordinat Cartesius → $sin = \dfrac{ordinat}{radius}$
$sin\; β = \dfrac{y}{r} = \dfrac{15}{17}$ → B.
$6.$ Perhatikan gambar dibawah! $Cos\ θ =$ . . . .
$A.\ \dfrac{7}{25}$
$B.\ -\dfrac{7}{25}$
$C.\ \dfrac{24}{25}$
$D.\ -\dfrac{24}{25}$
$E.\ -\dfrac{7}{24}$
$A.\ \dfrac{7}{25}$
$B.\ -\dfrac{7}{25}$
$C.\ \dfrac{24}{25}$
$D.\ -\dfrac{24}{25}$
$E.\ -\dfrac{7}{24}$
$x = 7,\ y = -24,\ r = 25$ (Phytagoras)
Koordinat Cartesius → $cos = \dfrac{absis}{radius}$
$cos\; θ = \dfrac{x}{r} = \dfrac{7}{25}$ → A.
Koordinat Cartesius → $cos = \dfrac{absis}{radius}$
$cos\; θ = \dfrac{x}{r} = \dfrac{7}{25}$ → A.
$7.$ Nilai dari $sin\ 30^{\circ}cos\ 60^{\circ} - cos\ 30^{\circ}sin\ 60^{\circ} =$ . . .
$A.\ \dfrac12$
$B.\ 1$
$C.\ -\dfrac12$
$D.\ -1$
$E.\ \dfrac12\sqrt{3}$
$A.\ \dfrac12$
$B.\ 1$
$C.\ -\dfrac12$
$D.\ -1$
$E.\ \dfrac12\sqrt{3}$
$sin\ 30^{\circ}cos\ 60^{\circ} - cos\ 30^{\circ}sin\ 60^{\circ}$ $= \dfrac{1}{2}.\dfrac{1}{2} - \dfrac{1}{2}\sqrt{3}.\dfrac{1}{2}\sqrt{3}$
$= \dfrac{1}{4} - \dfrac{3}{4}$
$= -\dfrac{1}{2}$ → C.
$= \dfrac{1}{4} - \dfrac{3}{4}$
$= -\dfrac{1}{2}$ → C.
$8.$ Nilai dari $\dfrac{tan\ 60^{\circ}sin\ 30^{\circ}}{cos\ 60^{\circ}} =$ . . . .
$A.\; 1$
$B.\; \sqrt{2}$
$C.\; \dfrac12\sqrt{3}$
$D.\; \sqrt{3}$
$E.\; 2$
$A.\; 1$
$B.\; \sqrt{2}$
$C.\; \dfrac12\sqrt{3}$
$D.\; \sqrt{3}$
$E.\; 2$
$\dfrac{tan\ 60^{\circ}sin\ 30^{\circ}}{cos\ 60^{\circ}}$ $= \dfrac{\sqrt{3}.\dfrac12}{\dfrac12}$
$= \sqrt{3}$ → D.
$= \sqrt{3}$ → D.
$9.$ Jika $tan\; α = \sqrt{3}$, maka $cos\; α =$ . . . .
$A.\; 0$
$B.\; \dfrac12$
$C.\; \sqrt{2}$
$D.\; \dfrac12\sqrt{3}$
$E.\; 1$
$A.\; 0$
$B.\; \dfrac12$
$C.\; \sqrt{2}$
$D.\; \dfrac12\sqrt{3}$
$E.\; 1$
$10.$ Nilai dari $2sin\dfrac{\pi}{3}cos\dfrac{\pi}{6} =$ . . . .
$A.\; \dfrac12$
$B.\; \sqrt{2}$
$C.\; \dfrac32$
$D.\; \sqrt{3}$
$E.\; 2$
$A.\; \dfrac12$
$B.\; \sqrt{2}$
$C.\; \dfrac32$
$D.\; \sqrt{3}$
$E.\; 2$
$2sin\ \dfrac{\pi}{3}cos\ \dfrac{\pi}{6}$ $= 2sin\ 60^{\circ}cos\ 30^{\circ}$
$= 2.\dfrac{1}{2}\sqrt{3}.\dfrac{1}{2}\sqrt{3}$
$= 2.\dfrac{3}{4}$
$= \dfrac{3}{2}$ → C.
$= 2.\dfrac{1}{2}\sqrt{3}.\dfrac{1}{2}\sqrt{3}$
$= 2.\dfrac{3}{4}$
$= \dfrac{3}{2}$ → C.
$11$. Perhatikan gambar dibawah ! Jika $cos\ P = \dfrac{1}{2}\sqrt{3}$, maka $3mn =$ . . . .
$A.\ 6$
$B.\ 8$
$C.\ 10$
$D.\ 12$
$E.\ 14$
$A.\ 6$
$B.\ 8$
$C.\ 10$
$D.\ 12$
$E.\ 14$
$cos\; P = \dfrac{\sqrt{3}}{2}$
$P = 30^{\circ}$
$cos\; P = \dfrac{2}{n}$
$\dfrac{\sqrt{3}}{2} = \dfrac{2}{n}$
$n = \dfrac{4}{3}\sqrt{3}$
$tan \;30^{\circ} = \dfrac{m}{2}$
$\dfrac{1}{3}\sqrt{3} = \dfrac{m}{2}$
$m = \dfrac{2}{3}\sqrt{3}$
$3mn = 3.\dfrac{2}{3}\sqrt{3}.\dfrac{4}{3}\sqrt{3}$
$= 8$ → B.
$P = 30^{\circ}$
$cos\; P = \dfrac{2}{n}$
$\dfrac{\sqrt{3}}{2} = \dfrac{2}{n}$
$n = \dfrac{4}{3}\sqrt{3}$
$tan \;30^{\circ} = \dfrac{m}{2}$
$\dfrac{1}{3}\sqrt{3} = \dfrac{m}{2}$
$m = \dfrac{2}{3}\sqrt{3}$
$3mn = 3.\dfrac{2}{3}\sqrt{3}.\dfrac{4}{3}\sqrt{3}$
$= 8$ → B.
$12$. Jika $sin \;\dfrac{1}{2}\alpha = \dfrac{1}{2}$ dengan $0^{\circ} < \alpha < 90^{\circ}$. Maka $cos\ α =$ . . . .
$A.\ \dfrac18$
$B.\ \dfrac14$
$C.\ \dfrac12$
$D.\ 1$
$E.\ 2$
$A.\ \dfrac18$
$B.\ \dfrac14$
$C.\ \dfrac12$
$D.\ 1$
$E.\ 2$
$sin \;\dfrac{1}{2}α = sin \;30^{\circ}$
$\dfrac{1}{2}α = 30^{\circ}$
$α = 60^{\circ}$
$cos\ 60 = \dfrac12$ → C.
$\dfrac{1}{2}α = 30^{\circ}$
$α = 60^{\circ}$
$cos\ 60 = \dfrac12$ → C.
$13$. Jika $tan\ x = m$ dengan $90^{\circ} < x < 180^{\circ}$. Maka $sin\ x cos\ x =$ . . . .
$A. \;\sqrt{1 + m^{2}}$
$B. \;\sqrt{1 - m^{2}}$
$C. \;\dfrac{m}{1 + m^{2}}$
$D. \;\dfrac{-m}{1 + m^{2}}$
$E. \;\dfrac{-m}{\sqrt{1 + m^{2}}}$
$A. \;\sqrt{1 + m^{2}}$
$B. \;\sqrt{1 - m^{2}}$
$C. \;\dfrac{m}{1 + m^{2}}$
$D. \;\dfrac{-m}{1 + m^{2}}$
$E. \;\dfrac{-m}{\sqrt{1 + m^{2}}}$
Perhatikan segitiga siku-sikunya!
Karena $tan\ x = m$ di kuadran II, maka $m$ pastilah bernilai negatif. Nilai sinus di kuadran II adalah positif. Supaya nilai sinus menjad positif, maka:
$sin\; x = -\dfrac{m}{\sqrt{1 + m^{2}}}$
$Cos\ x$ di kuadran II bernilai negatif, maka:
$cos\; x = -\dfrac{1}{\sqrt{1 + m^{2}}}$
$sin\; x.cos\; x = -\dfrac{m}{\sqrt{1 + m^{2}}}$.$\left(-\dfrac{1}{\sqrt{1 + m^{2}}}\right)$
$= \dfrac{m}{1 + m^{2}}$ → C.
Karena $tan\ x = m$ di kuadran II, maka $m$ pastilah bernilai negatif. Nilai sinus di kuadran II adalah positif. Supaya nilai sinus menjad positif, maka:
$sin\; x = -\dfrac{m}{\sqrt{1 + m^{2}}}$
$Cos\ x$ di kuadran II bernilai negatif, maka:
$cos\; x = -\dfrac{1}{\sqrt{1 + m^{2}}}$
$sin\; x.cos\; x = -\dfrac{m}{\sqrt{1 + m^{2}}}$.$\left(-\dfrac{1}{\sqrt{1 + m^{2}}}\right)$
$= \dfrac{m}{1 + m^{2}}$ → C.
$14$. Jika $cos\ α = -\dfrac12$ dan $α$ berada di kuadran II, maka $tan\ α =$ . . . .
$A.\ 0$
$B.\ \dfrac{1}{3}\sqrt{3}$
$C.\ -\sqrt{3}$
$D.\ \sqrt{3}$
$E.\ -1$
$A.\ 0$
$B.\ \dfrac{1}{3}\sqrt{3}$
$C.\ -\sqrt{3}$
$D.\ \sqrt{3}$
$E.\ -1$
$cos\; α = -\dfrac{1}{2}$ dan $α$ berada di kuadran II. Berarti $α = 120^{\circ}$
$tan \;120^{\circ} = tan \;(180^{\circ} - 60^{\circ})$
$= -tan\;60^{\circ}$
$= -\sqrt{3}$ → C.
$tan \;120^{\circ} = tan \;(180^{\circ} - 60^{\circ})$
$= -tan\;60^{\circ}$
$= -\sqrt{3}$ → C.
$15$. Jika $sin\ θ.cos\ θ > 0$, maka $θ$ berada di kuadran . . . .
$A.\ I\ dan\ II$
$B.\ I\ dan\ III$
$C.\ I\ dan\ IV$
$D.\ II\ dan\ III$
$E.\ III\ dan\ IV$
$A.\ I\ dan\ II$
$B.\ I\ dan\ III$
$C.\ I\ dan\ IV$
$D.\ II\ dan\ III$
$E.\ III\ dan\ IV$
$sin\ θ.cos\ θ > 0$
Supaya $sin\ θ.cos\ θ > 0$ (positif), maka:
$(i).\ sin\ θ > 0$ (positif) dan $cos\ θ > 0$ (positif).
berarti $θ$ ada di kuadran I.
$(ii).\ sin\ θ < 0$ (negatif) dan $cos\ θ < 0$ (negatif).
berarti $θ$ ada di kuadran III. → B.
Supaya $sin\ θ.cos\ θ > 0$ (positif), maka:
$(i).\ sin\ θ > 0$ (positif) dan $cos\ θ > 0$ (positif).
berarti $θ$ ada di kuadran I.
$(ii).\ sin\ θ < 0$ (negatif) dan $cos\ θ < 0$ (negatif).
berarti $θ$ ada di kuadran III. → B.
$16$. Jika $cosec\; α = -\sqrt{2}$ dengan $180^{\circ} < \alpha < 270^{\circ}$, maka $tan\ α =$ . . . .
$A.\ 0$
$B.\ -\dfrac12\sqrt{2}$
$C.\ -\sqrt{2}$
$D.\ -1$
$E.\ 1$
$A.\ 0$
$B.\ -\dfrac12\sqrt{2}$
$C.\ -\sqrt{2}$
$D.\ -1$
$E.\ 1$
$cosec\; α = -\sqrt{2}$ di kuadran III,
berarti $α = 225^{\circ}$
$tan \;225^{\circ} = tan \;(180^{\circ} + 45^{\circ})$
$= tan \;45^{\circ}$
$= 1$ → E.
berarti $α = 225^{\circ}$
$tan \;225^{\circ} = tan \;(180^{\circ} + 45^{\circ})$
$= tan \;45^{\circ}$
$= 1$ → E.
$17$. Nilai dari $\dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{cos\ 15^{\circ}} =$ . . . .
$A.\ 0$
$B.\ \dfrac12$
$C.\ \sqrt{2}$
$D.\ 1$
$E.\ \sqrt{3}$
$A.\ 0$
$B.\ \dfrac12$
$C.\ \sqrt{2}$
$D.\ 1$
$E.\ \sqrt{3}$
$\dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{cos\ 15^{\circ}}$
$= \dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{cos\ (90 - 75)^{\circ}}$
$= \dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{sin\ 75^{\circ}}$
$= sin\ 30^{\circ}$
$= \dfrac{1}{2}$ → B.
$= \dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{cos\ (90 - 75)^{\circ}}$
$= \dfrac{sin\ 30^{\circ}sin\ 75^{\circ}}{sin\ 75^{\circ}}$
$= sin\ 30^{\circ}$
$= \dfrac{1}{2}$ → B.
$18$. Jika $sin\; (2x - 10) = cos\; (64 + x)$, maka $x =$ . . . .
$A.\ 10^{\circ}$
$B.\ 11^{\circ}$
$C.\ 12^{\circ}$
$D.\ 13^{\circ}$
$E.\ 14^{\circ}$
$A.\ 10^{\circ}$
$B.\ 11^{\circ}$
$C.\ 12^{\circ}$
$D.\ 13^{\circ}$
$E.\ 14^{\circ}$
$sin \;(2x - 10^{\circ}) = cos \;(64^{\circ} + x)$
$cos \;( 90^{\circ} - (2x - 10^{\circ})) = cos \;(64^{\circ} + x)$
$cos \;(100^{\circ} - 2x) = cos \;(64^{\circ} + x)$
$100^{\circ} - 2x = 64^{\circ} + x$
$36^{\circ} = 3x$
$x = 12^{\circ}$ → C.
$cos \;( 90^{\circ} - (2x - 10^{\circ})) = cos \;(64^{\circ} + x)$
$cos \;(100^{\circ} - 2x) = cos \;(64^{\circ} + x)$
$100^{\circ} - 2x = 64^{\circ} + x$
$36^{\circ} = 3x$
$x = 12^{\circ}$ → C.
$19$. Diketahui segitiga ABC sembarang. $cos \;\dfrac{1}{2}(A + B) =$ . . . .
$A.\; cos\ C$
$B.\; cos\ \dfrac{1}{2}C$
$C.\; sin\ C$
$D.\; Sin\ \dfrac{1}{2}C$
$E.\; sin\ 2C$
$A.\; cos\ C$
$B.\; cos\ \dfrac{1}{2}C$
$C.\; sin\ C$
$D.\; Sin\ \dfrac{1}{2}C$
$E.\; sin\ 2C$
$A + B + C = 180$
$A + B = 180 - C$
$\dfrac12(A + B) = \dfrac12(180 - C)$
$\dfrac12(a + B) = (90 - \dfrac12C)$
$cos\ \dfrac12(A + B) = cos\ (90 - \dfrac12C)$
$cos\ \dfrac12(A + B) = sin\ \dfrac12C$ → D.
$A + B = 180 - C$
$\dfrac12(A + B) = \dfrac12(180 - C)$
$\dfrac12(a + B) = (90 - \dfrac12C)$
$cos\ \dfrac12(A + B) = cos\ (90 - \dfrac12C)$
$cos\ \dfrac12(A + B) = sin\ \dfrac12C$ → D.
$20.$ Jika $sin \;15^{\circ} = a$, maka $cos \;75^{\circ} =$ . . . .
$A.\ a + 1$
$B.\ a - 1$
$C.\ a$
$D.\ 1 - a$
$E.\ -a$
$A.\ a + 1$
$B.\ a - 1$
$C.\ a$
$D.\ 1 - a$
$E.\ -a$
$sin\ 15 = a$.
$cos\ 75 = cos\ (90 - 15)$
$= sin 15$
$= a$ → C.
$cos\ 75 = cos\ (90 - 15)$
$= sin 15$
$= a$ → C.
$21.$ Nilai dari $sin\ 135 + cos\ 135 + tan\ 135 =$ . . . .
$A.\ -1$
$B.\ 0$
$C.\; -\dfrac12\sqrt{2}$
$D.\; \dfrac12\sqrt{2}$
$E.\ 1$
$A.\ -1$
$B.\ 0$
$C.\; -\dfrac12\sqrt{2}$
$D.\; \dfrac12\sqrt{2}$
$E.\ 1$
$sin\ 135 + cos\ 135 + tan\ 135$ $= sin\ (180 - 45) + cos\ (180 - 45) + tan\ (180 - 45)$
$= sin\ 45 - cos\ 45 - tan\ 45$
$= \dfrac{1}{2}\sqrt{2} - \dfrac{1}{2}\sqrt{2} - 1$
$= -1$ → D.
$= sin\ 45 - cos\ 45 - tan\ 45$
$= \dfrac{1}{2}\sqrt{2} - \dfrac{1}{2}\sqrt{2} - 1$
$= -1$ → D.
$22.$ Jika $sin \;A = \dfrac12\sqrt{3}$ dan $A$ sudut tumpul, maka $cos\ A =$ . . . .
$A.\ -\dfrac12$
$B.\ \dfrac12$
$C.\ -\dfrac12\sqrt{2}$
$D.\ \dfrac12\sqrt{2}$
$E.\ -\dfrac12\sqrt{3}$
$A.\ -\dfrac12$
$B.\ \dfrac12$
$C.\ -\dfrac12\sqrt{2}$
$D.\ \dfrac12\sqrt{2}$
$E.\ -\dfrac12\sqrt{3}$
$sin\; A = \dfrac12\sqrt{3}$ dan $A$ sudut tumpul,
berarti $A = 120^{\circ}$
$cos\ 120^o = cos\ (180 - 60)^o$
$= -cos\ 60^o$
$= -\dfrac{1}{2}$ → A.
berarti $A = 120^{\circ}$
$cos\ 120^o = cos\ (180 - 60)^o$
$= -cos\ 60^o$
$= -\dfrac{1}{2}$ → A.
$23$. Jika $cos\ x = -\dfrac45$ untuk $0^{\circ} < x < 180^{\circ}$, maka $sin\ x =$ . . . .
$A.\ -\dfrac35$
$B.\ \dfrac35$
$C.\ -\dfrac45$
$D.\ -\dfrac53$
$E.\ 1$
$A.\ -\dfrac35$
$B.\ \dfrac35$
$C.\ -\dfrac45$
$D.\ -\dfrac53$
$E.\ 1$
berdasarkan koordinat cartesius, kuadran II:
$absis = -4 → a = -4.$
$radius = 5 → r = 5.$
Dengan Dalil Phytagoras, maka:
$ordinat = 3 → b = 3.$
$sin\ x = \dfrac{ordinat}{radius}$
$sin\ x = \dfrac br$
$= \dfrac35$ → B.
$absis = -4 → a = -4.$
$radius = 5 → r = 5.$
Dengan Dalil Phytagoras, maka:
$ordinat = 3 → b = 3.$
$sin\ x = \dfrac{ordinat}{radius}$
$sin\ x = \dfrac br$
$= \dfrac35$ → B.
$24$. Jika $sin\ 23 = m$, maka $cos\ 113 =$ . . . .
$A.\ m$
$B.\ -m$
$C.\ m + 1$
$D.\ 1 - m$
$E.\ \dfrac 1m$
$A.\ m$
$B.\ -m$
$C.\ m + 1$
$D.\ 1 - m$
$E.\ \dfrac 1m$
$cos\ 113 = cos\ (90 + 23)$
$= - sin\ 23$
$= -m$ → B.
$= - sin\ 23$
$= -m$ → B.
$25$. Nilai dari $\dfrac{sin\ 45^{\circ}sin\ 15^{\circ}}{cos\ 135^{\circ}cos\ 105^{\circ}}$ = . . . .
$A.\ -2$
$B.\ -1$
$C.\ 0$
$D.\ 1$
$E.\ 2$
$A.\ -2$
$B.\ -1$
$C.\ 0$
$D.\ 1$
$E.\ 2$
$\dfrac{sin\ 45^{\circ}sin\ 15^{\circ}}{cos\ 135^{\circ}cos\ 105^{\circ}}$
$= \dfrac{sin\ 45sin\ 15}{cos\ (180 - 45)cos\ (90 + 15)}$
$= \dfrac{sin\ 45sin\ 15}{(-cos\ 45)(-sin\ 15)}$
$= \dfrac{sin\ 45sin\ 15}{cos\ 45sin\ 15}$
$= tan\ 45$
$= 1$ → D.
$= \dfrac{sin\ 45sin\ 15}{cos\ (180 - 45)cos\ (90 + 15)}$
$= \dfrac{sin\ 45sin\ 15}{(-cos\ 45)(-sin\ 15)}$
$= \dfrac{sin\ 45sin\ 15}{cos\ 45sin\ 15}$
$= tan\ 45$
$= 1$ → D.
$26$. Nilai dari $tan \;\;200^{\circ} =$ . . . .
$A.\ -tan\ 20$
$B.\ tan\ 20$
$C.\ -cot\ 20$
$D.\ cot\ 20$
$E.\ 1 - tan\ 20$
$A.\ -tan\ 20$
$B.\ tan\ 20$
$C.\ -cot\ 20$
$D.\ cot\ 20$
$E.\ 1 - tan\ 20$
$tan\ 200 = tan\ (180 + 20)$
$= tan\ 20$ → B.
$= tan\ 20$ → B.
$27$. Jika $sin\ (π + A) = m$ dengan $A$ sudut lancip. Maka $cos\ A =$ . . . .
$A.\ -m$
$B.\ m$
$C.\ 1 - m$
$D.\ \sqrt{1 - m^{2}}$
$E.\ -\sqrt{1 - m^{2}}$
$A.\ -m$
$B.\ m$
$C.\ 1 - m$
$D.\ \sqrt{1 - m^{2}}$
$E.\ -\sqrt{1 - m^{2}}$
$28$. Jika $cos \;25^{\circ} = a$, maka $cos\ 295^{\circ} =$ . . . .
$A.\ -a$
$B.\ a$
$C.\ \sqrt{1 + a^{2}}$
$D.\ \sqrt{1 - a^{2}}$
$E.\ 1$
$A.\ -a$
$B.\ a$
$C.\ \sqrt{1 + a^{2}}$
$D.\ \sqrt{1 - a^{2}}$
$E.\ 1$
$29$. Diketahui $sin\ α + cos\ α = 2p$. Maka nilai dari $2sin\ α cos\ α =$ . . . .
$A.\; 2p - 1$
$B.\; 1 - 2p$
$C.\; 1 - 4p^{2}$
$D.\; 4p^{2} - 1$
$E. 1 - 2p^{2}$
$A.\; 2p - 1$
$B.\; 1 - 2p$
$C.\; 1 - 4p^{2}$
$D.\; 4p^{2} - 1$
$E. 1 - 2p^{2}$
$sin\; α + cos\; α = 2p$
$(sin \;α + cos \;α)^{2} = (2p)^{2}$
$(sin^{2}\; α + 2sin\;α.cos\;α + cos^{2}\; α) = 4p^{2}$
$1 + 2sin\;\alpha. cos\;\alpha = 4p^{2}$
Ingat!
$sin^{2}\;\alpha + cos^{2}\;\alpha = 1$
$2sin\;\alpha .cos\;\alpha = 4p^{2} - 1$ → D.
$(sin \;α + cos \;α)^{2} = (2p)^{2}$
$(sin^{2}\; α + 2sin\;α.cos\;α + cos^{2}\; α) = 4p^{2}$
$1 + 2sin\;\alpha. cos\;\alpha = 4p^{2}$
Ingat!
$sin^{2}\;\alpha + cos^{2}\;\alpha = 1$
$2sin\;\alpha .cos\;\alpha = 4p^{2} - 1$ → D.
$30.\; \dfrac{sin\; x.cos \;x}{tan\; x} =$ . . . .
$A. \;sin^{2}\; x$
$B. \;cos^{2}\; x$
$C. \;\dfrac{1}{sin\; x}$
$D. \;sin \;x$
$E. \;cos \;x$
$A. \;sin^{2}\; x$
$B. \;cos^{2}\; x$
$C. \;\dfrac{1}{sin\; x}$
$D. \;sin \;x$
$E. \;cos \;x$
$\dfrac{sin \;x.cos\; x}{tan\; x}$
$= \dfrac{sin \;x.cos\; x}{sin \;x/cos\; x}$
$= sin \;x.cos\; x.{\dfrac{cos\; x}{sin \;x}}$
$= cos^{2}\;x$ → B.
$= \dfrac{sin \;x.cos\; x}{sin \;x/cos\; x}$
$= sin \;x.cos\; x.{\dfrac{cos\; x}{sin \;x}}$
$= cos^{2}\;x$ → B.
$31.$ Pada segitiga $ABC$, diketahui sisi $a = 6\ cm$, $b = 10\ cm$, dan sudut $C = 60^{\circ}$. Luas segitiga tersebut sama dengan . . . .
$A.\; 10 \;cm^{2}$
$B.\; 15\; cm^{2}$
$C.\; 15\sqrt{3}\; cm^{2}$
$D.\; 20 \;cm^{2}$
$E.\; 20\sqrt{3}\; cm^{2}$
$A.\; 10 \;cm^{2}$
$B.\; 15\; cm^{2}$
$C.\; 15\sqrt{3}\; cm^{2}$
$D.\; 20 \;cm^{2}$
$E.\; 20\sqrt{3}\; cm^{2}$
$\begin{align}
L &= \dfrac{1}{2}absin\ C \\
&= \dfrac{1}{2}.6.10.sin\ 60 \\
&= \dfrac{1}{2}.6.10.\dfrac{1}{2}\sqrt{3}\\
&= 15\sqrt{3} → C.\\
\end{align}$
L &= \dfrac{1}{2}absin\ C \\
&= \dfrac{1}{2}.6.10.sin\ 60 \\
&= \dfrac{1}{2}.6.10.\dfrac{1}{2}\sqrt{3}\\
&= 15\sqrt{3} → C.\\
\end{align}$
$32$. Didalam suatu lingkaran dengan jari-jari $8$ cm dibuat segi enam beraturan. Luas segi enam beraturan tersebut sama dengan . . . .
$A.\; 16 \;cm^{2}$
$B.\; 32 \;cm^{2}$
$C.\; 64\sqrt{3} \;cm^{2}$
$D.\; 96\sqrt{2} \;cm^{2}$
$E.\; 96\sqrt{3} \;cm^{2}$
$A.\; 16 \;cm^{2}$
$B.\; 32 \;cm^{2}$
$C.\; 64\sqrt{3} \;cm^{2}$
$D.\; 96\sqrt{2} \;cm^{2}$
$E.\; 96\sqrt{3} \;cm^{2}$
$\begin{align}
L &= \dfrac{n}{2}R^{2}sin\ \dfrac{360}{n}\\
&= \dfrac{6}{2}.8^{2}.sin\ \frac{360}{6}\\
&= \dfrac{6}{2}.8^{2}.sin\ 60^o\\
&= 3.64.\frac{1}{2}\sqrt{3}\\
&= 96\sqrt{3} → E.\\
\end{align}$
L &= \dfrac{n}{2}R^{2}sin\ \dfrac{360}{n}\\
&= \dfrac{6}{2}.8^{2}.sin\ \frac{360}{6}\\
&= \dfrac{6}{2}.8^{2}.sin\ 60^o\\
&= 3.64.\frac{1}{2}\sqrt{3}\\
&= 96\sqrt{3} → E.\\
\end{align}$
$33$. Pada sebuah segitiga $ABC$, diketahui sudut $A = 30^{\circ}$ sudut $B = 45^{\circ}$, dan panjang sisi $a = 10$ cm. Maka panjang sisi $b =$ . . . .
$A.\; 5 \;cm$
$B.\; 5\sqrt{2} \;cm$
$C.\; 5\sqrt{3}\; cm$
$D.\; 10\sqrt{2}\; cm$
$E.\; 10\sqrt{3}\; cm$
$A.\; 5 \;cm$
$B.\; 5\sqrt{2} \;cm$
$C.\; 5\sqrt{3}\; cm$
$D.\; 10\sqrt{2}\; cm$
$E.\; 10\sqrt{3}\; cm$
$34$. Pada sebuah segitiga $ABC$, panjang $BC = 4$ cm dan $AC = 6\sqrt{2}\; cm.$ Panjang $AB =$ . . . .
$A. \;\sqrt{10}\; cm$
$B. \;2\sqrt{10}\; cm$
$C. \;\sqrt{15}\; cm$
$D. \;2\sqrt{15}\; cm$
$E.\; 3\sqrt{15}\; cm$
$A. \;\sqrt{10}\; cm$
$B. \;2\sqrt{10}\; cm$
$C. \;\sqrt{15}\; cm$
$D. \;2\sqrt{15}\; cm$
$E.\; 3\sqrt{15}\; cm$
$35$. Dari segitiga $ABC$ diketahui $a = 8\ cm,\ b = 6\ cm$. Jika luas segitiga adalah $12 \;cm^{2}$, maka besar sudut $C$ adalah . . . .
$A. \;120^{\circ}$
$B. \;90^{\circ}$
$C. \;60^{\circ}$
$D. \;45^{\circ}$
$E. \;30^{\circ}$
$A. \;120^{\circ}$
$B. \;90^{\circ}$
$C. \;60^{\circ}$
$D. \;45^{\circ}$
$E. \;30^{\circ}$
$36$. Diketahui $ΔABC$ dengan besar sudut $A = 60^{\circ}$, dan panjang $AB = 16\ cm$. Panjang $BC$ adalah . . . .
$A.\; 4\sqrt{4}\; cm$
$B.\; 6\sqrt{3}\; cm$
$C.\; 8\sqrt{6}\; cm$
$D.\; 16\sqrt{2}\; cm$
$E.\; 16\sqrt{3}\; cm$
$A.\; 4\sqrt{4}\; cm$
$B.\; 6\sqrt{3}\; cm$
$C.\; 8\sqrt{6}\; cm$
$D.\; 16\sqrt{2}\; cm$
$E.\; 16\sqrt{3}\; cm$
$37$. Jika $tan^{2}\;x + sec\;x = 5$ dengan $0 ≤ x ≤ \dfrac{\pi}{2}$ maka $cos\ x =$ . . . .
$A.\ 0$
$B.\ \dfrac12$
$C.\ \dfrac13$
$D.\ \dfrac12\sqrt{2}$
$E.\ \dfrac12\sqrt{3}$
$A.\ 0$
$B.\ \dfrac12$
$C.\ \dfrac13$
$D.\ \dfrac12\sqrt{2}$
$E.\ \dfrac12\sqrt{3}$
Ingat!
$1 + tan^2\ x = sec^2\ x$
$tan^{2}\;x + sec\;x = 5$
$sec^{2}\;x - 1 + sec\;x = 5$
$sec^{2}\;x + sec\;x - 6 = 0$
$(sec\;x + 3)(sec\;x - 2) = 0$
$sec\;x = -3\ atau\ sec\;x = 2$
karena $x$ berada di kuadran I, maka $sec\ x$ harus positif.
Jadi, $sec\ x = 2$ → $\dfrac{1}{cos\ x} = 2$
$cos\ x = \dfrac{1}{2}$ → B.
$1 + tan^2\ x = sec^2\ x$
$tan^{2}\;x + sec\;x = 5$
$sec^{2}\;x - 1 + sec\;x = 5$
$sec^{2}\;x + sec\;x - 6 = 0$
$(sec\;x + 3)(sec\;x - 2) = 0$
$sec\;x = -3\ atau\ sec\;x = 2$
karena $x$ berada di kuadran I, maka $sec\ x$ harus positif.
Jadi, $sec\ x = 2$ → $\dfrac{1}{cos\ x} = 2$
$cos\ x = \dfrac{1}{2}$ → B.
$38.\; \dfrac{tanA + tanB}{cotA + cotB}$ sama dengan . . . .
$A.\ cot\ A . cot\ B$
$B.\ tan\ A . tan\ B$
$C.\ sec\ A . sec\ B$
$D.\ tan\ A . tan\ B$
$E.\ tan\ A . cosec\ B$
$A.\ cot\ A . cot\ B$
$B.\ tan\ A . tan\ B$
$C.\ sec\ A . sec\ B$
$D.\ tan\ A . tan\ B$
$E.\ tan\ A . cosec\ B$
$\dfrac{tanA + tanB}{cotA + cotB}$ $= \dfrac{tanA + tanB}{1/tanA + 1/tanB}$
$= \dfrac{(tanA + tanB)}{(tanA + tanB)/tanAtanB}$
$= \dfrac{(tanA + tanB)}{(tanA + tanB)}.tanAtanB$
$= tanAtanB$ → B.
$= \dfrac{(tanA + tanB)}{(tanA + tanB)/tanAtanB}$
$= \dfrac{(tanA + tanB)}{(tanA + tanB)}.tanAtanB$
$= tanAtanB$ → B.
$39.\;sin^{4}\;x - cos^{4}\;x - 2sin^{2}\;x =$ . . . .
$A.\; -1$
$B.\; 0$
$C.\; 1$
$D.\; sin^{2}x - cos^{2}x$
$E.\; (sin^{2}x - cos^{2}x)^{2}$
$A.\; -1$
$B.\; 0$
$C.\; 1$
$D.\; sin^{2}x - cos^{2}x$
$E.\; (sin^{2}x - cos^{2}x)^{2}$
Ingat !
$sin^2\ x + cos^2\ x = 1$
$sin^{4}\;x - cos^{4}\;x - 2sin^{2}\;x$
$= (sin^{4}\;x - cos^{4}\;x) - 2sin^{2}\;x$
$= (sin^{2}\;x + cos^{2}\;x)(sin^{2}\;x - cos^{2}\;x) - 2sin^{2}x$
$= (sin^{2}\;x - cos^{2}\;x) - 2sin^{2}\;x$
$= -sin^{2}\;x - cos^{2}\;x$
$= -(sin^{2}\;x + cos^{2}\;x)$
$= -1$ → A.
$sin^2\ x + cos^2\ x = 1$
$sin^{4}\;x - cos^{4}\;x - 2sin^{2}\;x$
$= (sin^{4}\;x - cos^{4}\;x) - 2sin^{2}\;x$
$= (sin^{2}\;x + cos^{2}\;x)(sin^{2}\;x - cos^{2}\;x) - 2sin^{2}x$
$= (sin^{2}\;x - cos^{2}\;x) - 2sin^{2}\;x$
$= -sin^{2}\;x - cos^{2}\;x$
$= -(sin^{2}\;x + cos^{2}\;x)$
$= -1$ → A.
$40$. Koordinat kutub dari $P(4\sqrt{3},\; -4)$ adalah . . . .
$A.\; P(4, \;30^{\circ})$
$B.\; P(4, \;330^{\circ})$
$C.\; P(8, \;30^{\circ})$
$D.\; P(8, \;330^{\circ})$
$E.\; P(12, \;30^{\circ})$
$A.\; P(4, \;30^{\circ})$
$B.\; P(4, \;330^{\circ})$
$C.\; P(8, \;30^{\circ})$
$D.\; P(8, \;330^{\circ})$
$E.\; P(12, \;30^{\circ})$
$P(4\sqrt{3},\; -4)$ → titik P berada dikuadran IV.
$a = 4\sqrt{3}$
$b = -4$
$tan\;\theta = \dfrac{-4}{4\sqrt{3}} $
$tan\;\theta = -\dfrac{1}{\sqrt{3}} $
$tan\;\theta = -\dfrac{1}{3}\sqrt{3} $
karena $θ$ berada di kuadran IV, maka:
$\theta = (360 - 30)$
$\theta = 330^{\circ}$
$\begin{align}
r^{2} &= a^{2} + b^{2}\\
&= (4\sqrt{3})^{2} + 4^{2}\\
&= 64\\
r &= 8\\
\end{align}$
Jadi $P(8,\; 330^{\circ})$ → D.
$a = 4\sqrt{3}$
$b = -4$
$tan\;\theta = \dfrac{-4}{4\sqrt{3}} $
$tan\;\theta = -\dfrac{1}{\sqrt{3}} $
$tan\;\theta = -\dfrac{1}{3}\sqrt{3} $
karena $θ$ berada di kuadran IV, maka:
$\theta = (360 - 30)$
$\theta = 330^{\circ}$
$\begin{align}
r^{2} &= a^{2} + b^{2}\\
&= (4\sqrt{3})^{2} + 4^{2}\\
&= 64\\
r &= 8\\
\end{align}$
Jadi $P(8,\; 330^{\circ})$ → D.
Demikianlah soal dan pembahasan trigonometri SMA kelas 10, semoga bermanfaat. Selamat belajar !
Disusun oleh:
Joslin Sibarani
Alumni Teknik Sipil ITB
www.maretong.com






















Terimaka kasih banyak! pada amretong.com yang telah menyidiakan banyak materi soal dan latihan serta penenyelesaian semoga menjadi berkah tersendiri bagi segenap tim ...
ReplyDeleteTerimakasih, sangat bermanfaat
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteMakasih byk Kak mudah2an sya bisa lolos si itb aamiin :)
ReplyDeleteTerima kasih. sangat membantu.
ReplyDeletePuput lestari
ReplyDeleteP
ReplyDeleteterima kasih ya kak
ReplyDeleteSaya tidak tau apa yg salah karena saya masih SMA dan sekolah daring sehingga bnyk pelajaran yg tidak masuk, terimakasih bnyk buat kakak yg telah berbagi ilmu, saya jadi merasa terbantu memahami sedikit demi sedikit tentang trigonometri..semangat!!!
ReplyDeletehatur nuhun
ReplyDeleteThankyou buat soal soalnya,maretong
ReplyDelete