Soal dan Pembahasan Dimensi Tiga pada sesi ini adalah soal dan pembahasan tentang analisis bangun ruang sisi datar seperti kubus, balok, dan limas. Materi pokok dimensi tiga meliputi jarak antara titik dengan titik, jarak antara titik dengan garis, jarak antara titik dengan bidang, jarak antara garis dengan garis, jarak antara garis dengan bidang, jarak antara bidang dengan bidang, sudut antara garis dengan garis, sudut antara garis dengan bidang, dan sudut antara bidang dengan bidang. Materi ini sangat penting bagi kelas 12 untuk mempersiapkan diri menghadapi soal UN maupun soal Ujian Masuk PTN. Melihat betapa pentingnya soal UN dan UM PTN, maka untuk menyesuaikan dengan situasi, soal-soal yang disajikan di sini diambil dari soal-soal UN maupun Soal masuk PTN yang sudah pernah diujikan.
Soal dan Pembahasan Dimensi Tiga (analisis bangun ruang).
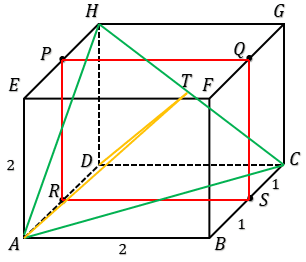
1. Diketahui kubus ABCD.EFGH dengan panjang rusuk 2. Jika bidang AFH dan CFH membagi kubus menjadi tiga buah ruang bagian, perbandingan volume ruang terkecil dengan volume kubus adalah . . . .
$A.\ 1 : 3$
$B.\ 1 : 4$
$C.\ 1 : 5$
$D.\ 1 : 6$
$E.\ 1 : 8$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2019 MtkIPA]
$A.\ 1 : 3$
$B.\ 1 : 4$
$C.\ 1 : 5$
$D.\ 1 : 6$
$E.\ 1 : 8$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2019 MtkIPA]
2. Diberikan kubus ABCD.EFGH dengan panjang rusuk 2. Titik P, Q, R, dan S berturut-turut adalah titik tengah dari EH, FG, AD, dan BC. Jika $\alpha$ adalah sudut antara bidang PQRS dan ACH, maka nilai $sin\ \alpha =$ . . . .
$A.\ \dfrac12\sqrt{6}$
$B.\ \dfrac13\sqrt{6}$
$C.\ \dfrac14\sqrt{6}$
$D.\ \dfrac15\sqrt{6}$
$E.\ \dfrac16\sqrt{6}$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2019 MtkIPA]
$A.\ \dfrac12\sqrt{6}$
$B.\ \dfrac13\sqrt{6}$
$C.\ \dfrac14\sqrt{6}$
$D.\ \dfrac15\sqrt{6}$
$E.\ \dfrac16\sqrt{6}$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2019 MtkIPA]
3. Diketahui kubus ABCD.EFGH dengan panjang rusuk $2\sqrt{2}$ cm. Jika titik P di tengah-tengah AB dan titik Q di tengah tengah BC, maka jarak antara titik H dengan garis PQ adalah . . . . cm.
$A.\ \sqrt{15}$
$B.\ 4$
$C.\ \sqrt{17}$
$D.\ 3\sqrt{2}$
$E.\ \sqrt{19}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2018 MtkIPA]
$A.\ \sqrt{15}$
$B.\ 4$
$C.\ \sqrt{17}$
$D.\ 3\sqrt{2}$
$E.\ \sqrt{19}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2018 MtkIPA]
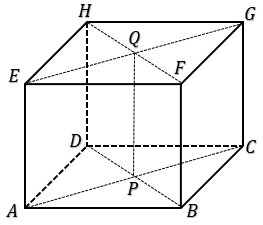
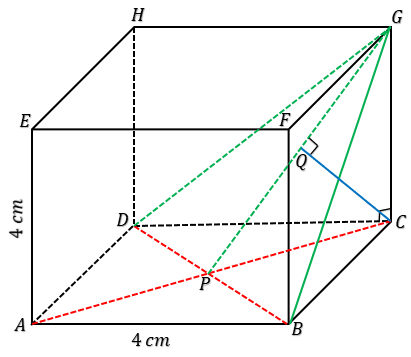
4. Diketahui kubus ABCD.EFGH dengan P dan Q berturut-turut adalah titik tengah HG dan BC. Jika panjang rusuk kubus tersebut
adalah 4 cm, maka jarak P ke Q adalah . . . . cm.
$(A)\ 2\sqrt{3}$
$(B)\ 2\sqrt{6}$
$(C)\ 6\sqrt{2}$
$(D)\ 6\sqrt{3}$
$(E)\ 6\sqrt{6}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2017 MDas]
adalah 4 cm, maka jarak P ke Q adalah . . . . cm.
$(A)\ 2\sqrt{3}$
$(B)\ 2\sqrt{6}$
$(C)\ 6\sqrt{2}$
$(D)\ 6\sqrt{3}$
$(E)\ 6\sqrt{6}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2017 MDas]
$PQ^2 = PG^2 + GC^2 + CQ^2$
$= 2^2 + 4^2 + 2^2$
$= 4 + 16 + 4$
$= 24$
$PQ = \sqrt{24}$
$= 2\sqrt{6}$
jawab: B.
$= 2^2 + 4^2 + 2^2$
$= 4 + 16 + 4$
$= 24$
$PQ = \sqrt{24}$
$= 2\sqrt{6}$
jawab: B.
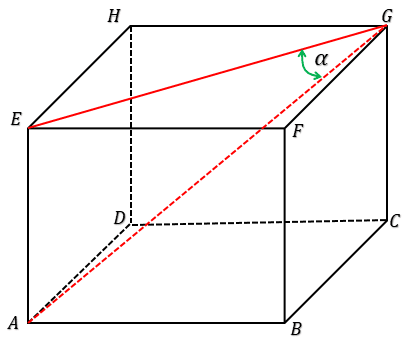
5. Diberikan kubus ABCD.EFGH dan P adalah titik tengah BC. Perbandingan luas segitiga APG dan luas segitiga DPG adalah . . . .
$A.\ 1 : 1$
$B.\ \sqrt{3} : \sqrt{2}$
$C.\ \sqrt{2} : 1$
$D.\ 3 : 2$
$E.\ \sqrt{3} : 1$
[Soal dan Pembahasan Dimensi Tiga UM UGM 2019 MtkIPA]
$A.\ 1 : 1$
$B.\ \sqrt{3} : \sqrt{2}$
$C.\ \sqrt{2} : 1$
$D.\ 3 : 2$
$E.\ \sqrt{3} : 1$
[Soal dan Pembahasan Dimensi Tiga UM UGM 2019 MtkIPA]
Misalkan panjang sisi kubus adalah $a$.
$\begin{align}
GP^2 &= CG^2 + CP^2\\
&= a^2 + \left(\dfrac12a\right)^2\\
&= a^2 + \dfrac14a^2\\
&= \dfrac54a^2\\
GP &= \dfrac12a\sqrt{5}\\
AG &= a\sqrt{3} → diagonal\ ruang\\
DG &= a\sqrt{2} → diagonal\ sisi\\
\end{align}$
Segitiga APG dan DPG adalah segitiga sama kaki.
$Luas\ \Delta APG = \dfrac12.a\sqrt{3}.\dfrac12a\sqrt{2} = \dfrac14a^2\sqrt{6}$
$Luas\ \Delta DPG = \dfrac12.a\sqrt{2}.\dfrac12a\sqrt{3} = \dfrac14a^2\sqrt{6}$
$Luas\ \Delta APD : Luas\ \Delta DPG = 1 : 1$
jawab: A.
6. Diketahui kubus ABCD.EFGH. Titik M berada di rusuk AB sedemikian sehingga $AM : BM = 2 : 1$. Titik N adalah titik tengah rusuk CD. Jika $\alpha$ adalah sudut yang terbentuk antara garis MC dan EN, maka nilai $cos\ \alpha = \cdots$
$A.\ \dfrac{7}{\sqrt{90}}$
$B.\ \dfrac{5}{\sqrt{30}}$
$C.\ \dfrac{7}{\sqrt{30}}$
$D.\ \dfrac{2\sqrt{20}}{9}$
$E.\ \dfrac{\sqrt{10}}{9}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2016 MtkIPA]
$A.\ \dfrac{7}{\sqrt{90}}$
$B.\ \dfrac{5}{\sqrt{30}}$
$C.\ \dfrac{7}{\sqrt{30}}$
$D.\ \dfrac{2\sqrt{20}}{9}$
$E.\ \dfrac{\sqrt{10}}{9}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2016 MtkIPA]
Untuk mempermudah perhitungan, anggap saja panjang sisi kubus adalah 6. Dengan demikian: BM = 2, MQ = 1, AQ = 3, FP = 3. Perlu diketahui bahwa sudut antara garis MC dan EN sama dengan sudut antara garis MC dan CP.
$CM^2 = CB^2 + BM^2$
$= 6^2 + 2^2$
$= 40$
$CM = 2\sqrt{10}$
$CP^2 = CG^2 + GF^2 + FP^2$
$= 6^2 + 6^2 + 3^2$
$= 36 + 36 + 9$
$= 81$
$CP = 9$
$MP^2 = MQ^2 + QP^2$
$= 1^2 + 6^2$
$= 1 + 36$
$= 37$
$MP = \sqrt{37}$
Perhatikan segitiga CMP ! Dengan menggunakan aturan cosinus:
$MP^2 = CM^2 + CP^2 - 2.CM.CP.cos\ \alpha$
$37 = 40 + 81 - 2.2\sqrt{10}.9.cos\ \alpha$
$37 = 121 - 36\sqrt{10}.cos\ \alpha$
$36\sqrt{10}.cos\ \alpha = 121 - 37$
$36\sqrt{10}.cos\ \alpha = 84$
$cos\ \alpha = \dfrac{7}{3\sqrt{10}} = \dfrac{7}{\sqrt{90}}$
jawab: A.
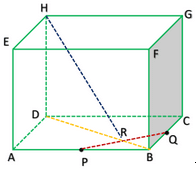
7. Diberikan kubus ABCD.EFGH dengan panjang rusuk 6. Di dalam kubus tersebut terdapat sebuah limas segiempat beraturan P.ABCD dengan tinggi 2. Bidang PBC membagi kubus menjadi dua bagian dengan perbandingan volume . . . .
$A.\ 1 : 2$
$B.\ 1 : 3$
$C.\ 2 : 3$
$D.\ 2 : 5$
$E.\ 3 : 5$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2017 MtkIPA]
$A.\ 1 : 2$
$B.\ 1 : 3$
$C.\ 2 : 3$
$D.\ 2 : 5$
$E.\ 3 : 5$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2017 MtkIPA]
Perhatikan gambar !
$\dfrac{UV}{PQ} = \dfrac{VW}{QW}$
$\dfrac{UV}{2} = \dfrac{6}{3}$
$UV = 4$
$AR = DS = UV = 4$
Bidang PBC terletak pada bidang BCSR, sehingga bidang PBC membagi kubus sama seperti bidang BCSR membagi kubus. Bidang BCSR membagi kubus menjadi dua bangun ruang yaitu ABCD.SR dan RBCS.EFGH.
Volume ABCD.SR $(V_1)$:
$V_1 = \dfrac12.AB.AR.AD$
$= \dfrac12.6.4.6$
$= 3.4.6$
Volume RBCS.EFGH $(V_2)$:
$V_2 = \dfrac{(ER + BF)}{2}.EF.FG$
$= \dfrac{2 + 6}{2}.6.6$
$= 4.6.6$
$\dfrac{V_1}{V_2} = \dfrac{3.4.6}{4.6.6} = \dfrac12$
$V_1 : V_2 = 1 : 2$
jawab: A.
$\dfrac{UV}{PQ} = \dfrac{VW}{QW}$
$\dfrac{UV}{2} = \dfrac{6}{3}$
$UV = 4$
$AR = DS = UV = 4$
Bidang PBC terletak pada bidang BCSR, sehingga bidang PBC membagi kubus sama seperti bidang BCSR membagi kubus. Bidang BCSR membagi kubus menjadi dua bangun ruang yaitu ABCD.SR dan RBCS.EFGH.
Volume ABCD.SR $(V_1)$:
$V_1 = \dfrac12.AB.AR.AD$
$= \dfrac12.6.4.6$
$= 3.4.6$
Volume RBCS.EFGH $(V_2)$:
$V_2 = \dfrac{(ER + BF)}{2}.EF.FG$
$= \dfrac{2 + 6}{2}.6.6$
$= 4.6.6$
$\dfrac{V_1}{V_2} = \dfrac{3.4.6}{4.6.6} = \dfrac12$
$V_1 : V_2 = 1 : 2$
jawab: A.
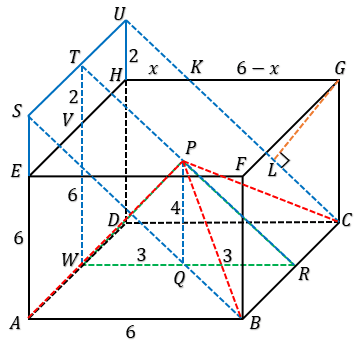
8. Diberikan kubus ABCD.EFGH dengan panjang rusuk 6. Di dalam kubus tersebut terdapat sebuah limas segiempat beraturan P.ABCD dengan tinggi 4. Jarak antara titik G dan bidang PBC adalah . . . .
$A.\ \dfrac{20}{5}$
$B.\ \dfrac{18}{5}$
$C.\ \dfrac{16}{5}$
$D.\ \dfrac{14}{5}$
$E.\ \dfrac{10}{5}$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2017 MtkIPA]
$A.\ \dfrac{20}{5}$
$B.\ \dfrac{18}{5}$
$C.\ \dfrac{16}{5}$
$D.\ \dfrac{14}{5}$
$E.\ \dfrac{10}{5}$
[Soal dan Pembahasan Dimensi Tiga SIMAK UI 2017 MtkIPA]
Perhatikan gambar !
$\dfrac{TW}{PQ} = \dfrac{WR}{QR}$
$\dfrac{TW}{4} = \dfrac{6}{3}$
$TW = 8$
$AS = DU = TW = 8$
$HU = 2$
$\dfrac{HU}{CG} = \dfrac{HK}{GK}$
$\dfrac{2}{6} = \dfrac{x}{6 - x}$
$2(6 - x) = 6x$
$12 - 2x = 6x$
$12 = 8x$
$x = \dfrac32$
$GK = 6 - x$
$= 6 - \dfrac32$
$= \dfrac92$
$CK^2 = CG^2 + GK^2$
$= 6^2 + \left(\dfrac92\right)^2$
$= 36 + \dfrac{81}{4}$
$= \dfrac{225}{4}$
$CK = \dfrac{15}{2}$
Karena bidang PBC terletak pada bidang BCUS, maka jarak antara titik G terhadap bidang PBC sama dengan jarak antara titik G dengan bidang BCUS. Jika titik G diproyeksikan terhadap bidang BCUS, maka titik hasil proyeksinya adalah titik L yang terletak pada garis CK, sehingga jarak antara titik G dengan bidang PBC adalah panjang garis GL. Dengan memperhatikan segitiga CGK, maka panjang garis GL bisa dihitung dengan rumus luas segitiga.
$\dfrac12.CG.GK = \dfrac12.CK.GL$
$CG.GK = CK.GL$
$6.\dfrac92 = \dfrac{15}{2}.GL$
$GL = \dfrac{6.9}{15}$
$= \dfrac{18}{5}$
jawab: B.
$\dfrac{TW}{PQ} = \dfrac{WR}{QR}$
$\dfrac{TW}{4} = \dfrac{6}{3}$
$TW = 8$
$AS = DU = TW = 8$
$HU = 2$
$\dfrac{HU}{CG} = \dfrac{HK}{GK}$
$\dfrac{2}{6} = \dfrac{x}{6 - x}$
$2(6 - x) = 6x$
$12 - 2x = 6x$
$12 = 8x$
$x = \dfrac32$
$GK = 6 - x$
$= 6 - \dfrac32$
$= \dfrac92$
$CK^2 = CG^2 + GK^2$
$= 6^2 + \left(\dfrac92\right)^2$
$= 36 + \dfrac{81}{4}$
$= \dfrac{225}{4}$
$CK = \dfrac{15}{2}$
Karena bidang PBC terletak pada bidang BCUS, maka jarak antara titik G terhadap bidang PBC sama dengan jarak antara titik G dengan bidang BCUS. Jika titik G diproyeksikan terhadap bidang BCUS, maka titik hasil proyeksinya adalah titik L yang terletak pada garis CK, sehingga jarak antara titik G dengan bidang PBC adalah panjang garis GL. Dengan memperhatikan segitiga CGK, maka panjang garis GL bisa dihitung dengan rumus luas segitiga.
$\dfrac12.CG.GK = \dfrac12.CK.GL$
$CG.GK = CK.GL$
$6.\dfrac92 = \dfrac{15}{2}.GL$
$GL = \dfrac{6.9}{15}$
$= \dfrac{18}{5}$
jawab: B.
9. Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P, Q, dan R berturut-turut merupakan titik tengah rusuk EH, BF, dan CG. Jarak titik P ke garis QR adalah . . . .
$A.\ 3\sqrt{7}\ cm$
$B.\ 3\sqrt{6}\ cm$
$C.\ 3\sqrt{5}\ cm$
$D.\ 3\sqrt{3}\ cm$
$E.\ 2\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPA]
$A.\ 3\sqrt{7}\ cm$
$B.\ 3\sqrt{6}\ cm$
$C.\ 3\sqrt{5}\ cm$
$D.\ 3\sqrt{3}\ cm$
$E.\ 2\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPA]
10. Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Jika titik P terletak pada pertengahan garis GC, jarak titik C ke bidang BPD adalah . . . .
$A.\ \dfrac53\sqrt{7}\ cm$
$B.\ \dfrac53\sqrt{6}\ cm$
$C.\ \dfrac53\sqrt{5}\ cm$
$D.\ \dfrac53\sqrt{3}\ cm$
$E.\ \dfrac53\sqrt{2}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPA]
$A.\ \dfrac53\sqrt{7}\ cm$
$B.\ \dfrac53\sqrt{6}\ cm$
$C.\ \dfrac53\sqrt{5}\ cm$
$D.\ \dfrac53\sqrt{3}\ cm$
$E.\ \dfrac53\sqrt{2}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPA]
Perhatikan gambar !
$AC = 10\sqrt{2}$ → Diagonal sisi.
$CQ = \dfrac12AC = 5\sqrt{2}$
$PQ^2 = CQ^2 + CP^2$
$= (5\sqrt{2})^2 + 5^2$
$= 75$
$PQ = 5\sqrt{3}$
Berdsarkan prinsip luas segitiga.
$\dfrac12.CR.PQ = \dfrac12.CQ.CP$
$CR = \dfrac{CQ.CP}{PQ}$
$CR = \dfrac{5\sqrt{2}.5}{5\sqrt{3}}$
$CR = \dfrac53\sqrt{6}$
jawab: B.
$AC = 10\sqrt{2}$ → Diagonal sisi.
$CQ = \dfrac12AC = 5\sqrt{2}$
$PQ^2 = CQ^2 + CP^2$
$= (5\sqrt{2})^2 + 5^2$
$= 75$
$PQ = 5\sqrt{3}$
Berdsarkan prinsip luas segitiga.
$\dfrac12.CR.PQ = \dfrac12.CQ.CP$
$CR = \dfrac{CQ.CP}{PQ}$
$CR = \dfrac{5\sqrt{2}.5}{5\sqrt{3}}$
$CR = \dfrac53\sqrt{6}$
jawab: B.
11. Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Jarak dari titik A ke bidang CDEF sama dengan jarak dari titik A ke . . . .
A. titik tengah ED
B. titik tengah EF
C. titik pusat bidang CDEF
D. titik E
E. titik D
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPS]
A. titik tengah ED
B. titik tengah EF
C. titik pusat bidang CDEF
D. titik E
E. titik D
[Soal dan Pembahasan Dimensi Tiga UN 2019 MtkIPS]
12. Jika luas bidang diagonal suatu kubus adalah $36\sqrt{2}\ cm^2$, panjang diagonal ruang kubus adalah . . . .
$A.\ 18\sqrt{3}$
$B.\ 15\sqrt{3}$
$C.\ 12\sqrt{3}$
$D.\ 9\sqrt{3}$
$E.\ 6\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2019 Mtk IPS]
$A.\ 18\sqrt{3}$
$B.\ 15\sqrt{3}$
$C.\ 12\sqrt{3}$
$D.\ 9\sqrt{3}$
$E.\ 6\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2019 Mtk IPS]
Perhatikan gambar bidang diagonal CDEF !
Misalkan panjang sisi kubus adalah $a$, sehingga panjang diagonal sisi kubus adalah $a\sqrt{2}$
$CD = a$
$DE = a\sqrt{2}$
$Luas\ bidang\ diagonal = CD\ \times\ DE$
$36\sqrt{2} = a.a\sqrt{2}$
$a^2 = \dfrac{36\sqrt{2}}{\sqrt{2}}$
$a^2 = 36$
$a = 6$
$Panjang\ diagonal\ ruang = a\sqrt{3}$
$Panjang\ diagonal\ ruang = 6\sqrt{3}$
jawab: E.
Misalkan panjang sisi kubus adalah $a$, sehingga panjang diagonal sisi kubus adalah $a\sqrt{2}$
$CD = a$
$DE = a\sqrt{2}$
$Luas\ bidang\ diagonal = CD\ \times\ DE$
$36\sqrt{2} = a.a\sqrt{2}$
$a^2 = \dfrac{36\sqrt{2}}{\sqrt{2}}$
$a^2 = 36$
$a = 6$
$Panjang\ diagonal\ ruang = a\sqrt{3}$
$Panjang\ diagonal\ ruang = 6\sqrt{3}$
jawab: E.
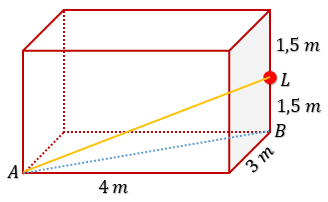
13. Kamar Andi berbentuk balok dengan panjang 4 m, lebar 3 m, dan tinggi 3 m. Andi memasang lampu di tengah-tengah rusuk tegak salah satu pertemuan di dinding kamarnya. Jarak sinar lampu terjauh di kamar Andi adalah . . . .
$A.\ \displaystyle \dfrac{1}{2}\sqrt{109}\ m$
$B.\ \displaystyle \dfrac{1}{2}\sqrt{106}\ m$
$C.\ \displaystyle \dfrac{1}{2}\sqrt{91}\ m$
$D.\ \displaystyle \dfrac{1}{4}\sqrt{109}\ m$
$E.\ \displaystyle \dfrac{1}{4}\sqrt{106}\ m$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPA]
$A.\ \displaystyle \dfrac{1}{2}\sqrt{109}\ m$
$B.\ \displaystyle \dfrac{1}{2}\sqrt{106}\ m$
$C.\ \displaystyle \dfrac{1}{2}\sqrt{91}\ m$
$D.\ \displaystyle \dfrac{1}{4}\sqrt{109}\ m$
$E.\ \displaystyle \dfrac{1}{4}\sqrt{106}\ m$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPA]
Jarak sinar lampu terjauh adalah AL.
$AB = 5\ m$
$AL^2 = AB^2 + BL^2$
$\displaystyle = 5^2 + \left(\dfrac{3}{2} \right)^2$
$\displaystyle = 25 + \left(\dfrac{9}{4} \right)$
$\displaystyle = \dfrac{109}{4}$
$\displaystyle AL = \sqrt{\dfrac{109}{4}}$
$\displaystyle = \dfrac{1}{2}\sqrt{109}\ m$
jawab: A.
14. Diketahui kubus ABCD.EFGH besar sudut antara DG
dan AE adalah . . . .
$A.\ 0^o$
$B.\ 30^o$
$C.\ 45^o$
$D.\ 60^o$
$E.\ 90^o$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPA]
dan AE adalah . . . .
$A.\ 0^o$
$B.\ 30^o$
$C.\ 45^o$
$D.\ 60^o$
$E.\ 90^o$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPA]
15. Besar sudut antara ruas garis AG dan bidang EFGH pada kubus ABCD.EFGH adalah $\alpha$. Nilai $cos \alpha$ adalah . . . .
$A.\ \dfrac{1}{3}\sqrt{3}$
$B.\ \dfrac{1}{2}\sqrt{3}$
$C.\ \dfrac{1}{3}\sqrt{6}$
$D.\ \dfrac{1}{2}\sqrt{6}$
$E.\ \dfrac{1}{3}\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
$A.\ \dfrac{1}{3}\sqrt{3}$
$B.\ \dfrac{1}{2}\sqrt{3}$
$C.\ \dfrac{1}{3}\sqrt{6}$
$D.\ \dfrac{1}{2}\sqrt{6}$
$E.\ \dfrac{1}{3}\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
16. Berikut ini adalah pernyataan-pernyataan tentang kubus ABCD.EFGH dengan P, Q, R berturut-turut titik-titik tengah rusuk AE, CG, dan DH.
(1) Ruas garis QE dan RF berpotongan
(2) Ruas garis QB dan PB tegak lurus
(3) Ruas garis QB dan HP tidak sejajar
(4) Segitiga PDQ samakaki
Pernyataan yang benar adalah . . . .
A. (1) dan (2)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
E. (3) dan (4)
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
(1) Ruas garis QE dan RF berpotongan
(2) Ruas garis QB dan PB tegak lurus
(3) Ruas garis QB dan HP tidak sejajar
(4) Segitiga PDQ samakaki
Pernyataan yang benar adalah . . . .
A. (1) dan (2)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
E. (3) dan (4)
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
Perhatikan gambar !
Perhatikan gambar di atas!
$\bullet$ Ruas garis QE dan RF pasti berpotongan.
$\bullet$ Ruas garis QB dan PB tidak tegak lurus. Panjang PQ = AC = $a\sqrt{2}$. Karena segitiga ABC siku-siku di B, tidak mungkin segitiga PBQ siku-siku di B, karena PB tidak sama dengan AB.
$\bullet$ Ruas garis QB dan HP adalah sejajar.
$\bullet$ Segitiga PDQ sama kaki. Panjang DP sama dengan DQ.
Jadi jawab yang benar adalah (1) dan (4).
jawab: B.
Perhatikan gambar di atas!
$\bullet$ Ruas garis QE dan RF pasti berpotongan.
$\bullet$ Ruas garis QB dan PB tidak tegak lurus. Panjang PQ = AC = $a\sqrt{2}$. Karena segitiga ABC siku-siku di B, tidak mungkin segitiga PBQ siku-siku di B, karena PB tidak sama dengan AB.
$\bullet$ Ruas garis QB dan HP adalah sejajar.
$\bullet$ Segitiga PDQ sama kaki. Panjang DP sama dengan DQ.
Jadi jawab yang benar adalah (1) dan (4).
jawab: B.
17. Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Titik P terletak di tengah diagonal sisi AC. Jarak dari titik C ke garis GP adalah . . . .
$A.\ 4\sqrt{3}$
$B.\ 4\sqrt{2}$
$C.\ 3\sqrt{3}$
$D.\ 3\sqrt{2}$
$E.\ 2\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
$A.\ 4\sqrt{3}$
$B.\ 4\sqrt{2}$
$C.\ 3\sqrt{3}$
$D.\ 3\sqrt{2}$
$E.\ 2\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2018 MtkIPS]
Perhatikan gambar di atas!
$AC = 6\sqrt{2}$ → $PC = \dfrac12AC = 3\sqrt{2}$
$PG^2 = PC^2 + CG^2$
$= (3\sqrt{2})^2 + 6^2$
$= 18 + 36$
$= 54$
$PG = \sqrt{54}$
$PG = 3\sqrt{6}$
Dengan menggunakan prinsip luas segitiga:
$CQ = \dfrac{PC.CG}{PG}$
$= \dfrac{3\sqrt{2}.6}{3\sqrt{6}}$
$= 2\sqrt{3}$
jawab: E.
Cara cepat:
Untuk soal yang sejenis, misalnya jarak antara titik A ke garis EP, jarak antara D ke garis HP, dan lain-lain, gunakan Rumus: $R = \dfrac{1}{3}a\sqrt{3}$
R → jarak, dan a panjang rusuk kubus.
Dari soal: $R = \dfrac{1}{3}.6.\sqrt{3} = 2\sqrt{3}$.
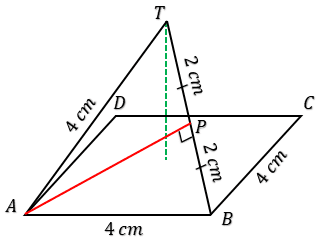
18. Diketahui limas beraturan T.ABCD. Panjang rusuk tegak dan panjang rusuk alas 4 cm. Jarak titik A ke TB adalah . . . .
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 4\ cm$
$D.\ 4\sqrt{2}\ cm$
$E.\ 4\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 4\ cm$
$D.\ 4\sqrt{2}\ cm$
$E.\ 4\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
19. Diketahui kubus KLMN.OPQR dengan panjang rusuk 6 cm. Jarak titik M ke bidang LNQ adalah . . . .
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 3\sqrt{2}\ cm$
$D.\ 3\sqrt{3}\ cm$
$E.\ 4\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 3\sqrt{2}\ cm$
$D.\ 3\sqrt{3}\ cm$
$E.\ 4\sqrt{3}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
Perhatikan gambar !
$KM = 6\sqrt{2}$ → Diagonal sisi.
$BM = \dfrac12KM$
$= \dfrac12.6\sqrt{2}$
$= 3\sqrt{2}$
$BQ^2 = BM^2 + MQ^2$
$= (3\sqrt{2})^2 + 6^2$
$= 18 + 36$
$= 54$
$BQ = \sqrt{54}$
$= 3\sqrt{6}$
Dengan prinsip luas segitiga:
$\dfrac12.BM.MQ = \dfrac12.BQ.AM$
$BM.MQ = BQ.AM$
$AM = \dfrac{BM.MQ}{BQ}$
$= \dfrac{3\sqrt{2}.6}{3\sqrt{6}}$
$= \dfrac{6\sqrt{2}}{\sqrt{6}}$
$= \sqrt{12}$
$= 2\sqrt{3}\ cm$
Rumus cepat:
$AM = \dfrac13a\sqrt{3}$ → $a = 6$ (panjang sisi kubus).
$AM = \dfrac13.6\sqrt{3} = 2\sqrt{3}\ cm$.
$KM = 6\sqrt{2}$ → Diagonal sisi.
$BM = \dfrac12KM$
$= \dfrac12.6\sqrt{2}$
$= 3\sqrt{2}$
$BQ^2 = BM^2 + MQ^2$
$= (3\sqrt{2})^2 + 6^2$
$= 18 + 36$
$= 54$
$BQ = \sqrt{54}$
$= 3\sqrt{6}$
Dengan prinsip luas segitiga:
$\dfrac12.BM.MQ = \dfrac12.BQ.AM$
$BM.MQ = BQ.AM$
$AM = \dfrac{BM.MQ}{BQ}$
$= \dfrac{3\sqrt{2}.6}{3\sqrt{6}}$
$= \dfrac{6\sqrt{2}}{\sqrt{6}}$
$= \sqrt{12}$
$= 2\sqrt{3}\ cm$
Rumus cepat:
$AM = \dfrac13a\sqrt{3}$ → $a = 6$ (panjang sisi kubus).
$AM = \dfrac13.6\sqrt{3} = 2\sqrt{3}\ cm$.
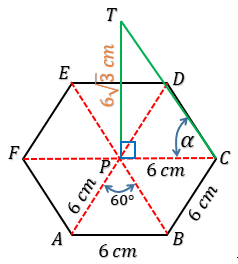
20. Diketahui limas segi enam beraturan T.ABCDEF rusuk alasnya 6 cm dan tinggi limas $6\sqrt{3}\ cm$. Nilai sinus sudut antara rusuk tegak dan bidang alas limas adalah . . . .
$A.\ \dfrac13\sqrt{2}$
$B.\ \dfrac12$
$C.\ \dfrac13\sqrt{3}$
$D.\ \dfrac12\sqrt{2}$
$E.\ \dfrac12\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
$A.\ \dfrac13\sqrt{2}$
$B.\ \dfrac12$
$C.\ \dfrac13\sqrt{3}$
$D.\ \dfrac12\sqrt{2}$
$E.\ \dfrac12\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
21. Diketahui kubus ABCD.EFGH, panjang rusuknya 12 cm dan $\alpha$ adalah sudut antara bidang BDG dan ABCD. Nilai $sin\ \alpha$ adalah . . . .
$A.\ \dfrac16\sqrt{6}$
$B.\ \dfrac13\sqrt{3}$
$C.\ \dfrac12\sqrt{2}$
$D.\ \dfrac13\sqrt{6}$
$E.\ \dfrac12\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
$A.\ \dfrac16\sqrt{6}$
$B.\ \dfrac13\sqrt{3}$
$C.\ \dfrac12\sqrt{2}$
$D.\ \dfrac13\sqrt{6}$
$E.\ \dfrac12\sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPA]
Perhatikan gambar !
$AC = 12\sqrt{2}$ → Diagonal sisi
$PC = \dfrac12AC$
$= \dfrac12.12\sqrt{2}$
$= 6\sqrt{2}$
$PG^2 = PC^2 + CG^2$
$= (6\sqrt{2})^2 + 12^2$
$= 72 + 144$
$= 216$
$= 36.6$
$PG = \sqrt{36.6}$
$= 6\sqrt{6}$
$sin\ \alpha = \dfrac{CG}{PC}$
$= \dfrac{12}{6\sqrt{6}}$
$= \dfrac{2}{\sqrt{6}}$
$= \dfrac13\sqrt{6}$
jawab: D.
$AC = 12\sqrt{2}$ → Diagonal sisi
$PC = \dfrac12AC$
$= \dfrac12.12\sqrt{2}$
$= 6\sqrt{2}$
$PG^2 = PC^2 + CG^2$
$= (6\sqrt{2})^2 + 12^2$
$= 72 + 144$
$= 216$
$= 36.6$
$PG = \sqrt{36.6}$
$= 6\sqrt{6}$
$sin\ \alpha = \dfrac{CG}{PC}$
$= \dfrac{12}{6\sqrt{6}}$
$= \dfrac{2}{\sqrt{6}}$
$= \dfrac13\sqrt{6}$
jawab: D.
22. Jarak titik B ke bidang ACGE pada kubus ABCD.EFGH adalah . . . .
A. PQ
B. BP
C. BC
D. BA
E. BG
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPS]
A. PQ
B. BP
C. BC
D. BA
E. BG
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPS]
Proyeksi titik B ke bidang ACGE adalah titik P, sehingga jarak antara titik B dengan bidang ACGE adalah BP.
jawab: B.
jawab: B.
23. Besar sudut antara AH dan CH pada kubus ABCD.EFGH berikut adalah . . . .
$A.\ 90^o$
$B.\ 60^o$
$C.\ 45^o$
$D.\ 30^o$
$E.\ 0^o$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPS]
$A.\ 90^o$
$B.\ 60^o$
$C.\ 45^o$
$D.\ 30^o$
$E.\ 0^o$
[Soal dan Pembahasan Dimensi Tiga UN 2017 MtkIPS]
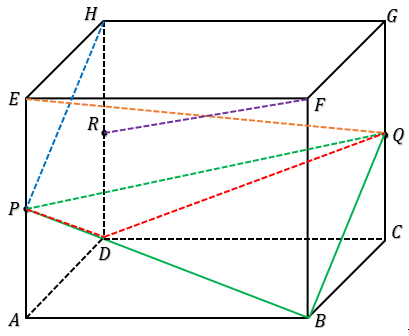
24. Diberikan kubus ABCD.EFGH dengan panjang rusuk 2 cm. Jika P titik tengah AB, Q titik tengah CG dan R terletak pada PD sehingga QR tegak lurus dengan PD, maka QR adalah . . . . cm
$A.\ \sqrt{\dfrac{21}{5}}$
$B.\ \sqrt{\dfrac{21}{6}}$
$C.\ \sqrt{\dfrac{21}{9}}$
$D.\ \sqrt{\dfrac{21}{12}}$
$E.\ \sqrt{\dfrac{21}{15}}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2019 MS]
$A.\ \sqrt{\dfrac{21}{5}}$
$B.\ \sqrt{\dfrac{21}{6}}$
$C.\ \sqrt{\dfrac{21}{9}}$
$D.\ \sqrt{\dfrac{21}{12}}$
$E.\ \sqrt{\dfrac{21}{15}}$
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2019 MS]
Perhatikan gambar !
$DP = DQ = \sqrt{DA^2 + AP^2}$
$= \sqrt{2^2 + 1^2}$
$= \sqrt{5}$
$PQ = \sqrt{PB^2 + BC^2 + CQ^2}$
$= \sqrt{1^2 + 2^2 + 1^2}$
$= \sqrt{6}$
$\dfrac12.PQ.DT = \dfrac12.DP.QR$
$PQ.DT = DP.QR$
$QR = \dfrac{PQ.DT}{DP}$
$= \dfrac{\sqrt{6}.\sqrt{\dfrac72}}{\sqrt{5}}$
$= \sqrt{\dfrac{21}{5}}$
jawab: A.
$DP = DQ = \sqrt{DA^2 + AP^2}$
$= \sqrt{2^2 + 1^2}$
$= \sqrt{5}$
$PQ = \sqrt{PB^2 + BC^2 + CQ^2}$
$= \sqrt{1^2 + 2^2 + 1^2}$
$= \sqrt{6}$
$\dfrac12.PQ.DT = \dfrac12.DP.QR$
$PQ.DT = DP.QR$
$QR = \dfrac{PQ.DT}{DP}$
$= \dfrac{\sqrt{6}.\sqrt{\dfrac72}}{\sqrt{5}}$
$= \sqrt{\dfrac{21}{5}}$
jawab: A.
25. Diketahui limas segiempat beraturan T.ABCD dengan $AB = BC = 5\sqrt{2}$ cm dan $TA = 13$ cm. Jarak titik A ke garis TC adalah . . . .
$A.\ 4\dfrac{8}{13}\ cm$
$B.\ 4\dfrac{12}{13}\ cm$
$C.\ 9\dfrac{3}{13}\ cm$
$D.\ 10\ cm$
$E.\ 12\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2016 MtkIPA]
$A.\ 4\dfrac{8}{13}\ cm$
$B.\ 4\dfrac{12}{13}\ cm$
$C.\ 9\dfrac{3}{13}\ cm$
$D.\ 10\ cm$
$E.\ 12\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2016 MtkIPA]
Perhatikan gambar !
$AC^2 = AB^2 + BC^2$
$= (5\sqrt{2})^2 + (5\sqrt{2})^2$
$= 50 + 50$
$= 100$
$AC = \sqrt{100}$
$= 10\ cm$
Segitiga ACT merupakan segitiga sama kaki, sehingga AP = CP = 5 cm.
$PT^2 = AT^2 - AP^2$
$= 13^2 - 5^2$
$= 169 - 25$
$= 144$
$PT = \sqrt{144}$
$= 12\ cm$
$\dfrac12.AC.PT = \dfrac12.CT.AE$
$AC.PT = CT.AE$
$AE = \dfrac{AC.PT}{CT}$
$= \dfrac{10.12}{13}$
$= \dfrac{120}{13}$
$= 9\dfrac{3}{13}\ cm$
jawab: C.
$AC^2 = AB^2 + BC^2$
$= (5\sqrt{2})^2 + (5\sqrt{2})^2$
$= 50 + 50$
$= 100$
$AC = \sqrt{100}$
$= 10\ cm$
Segitiga ACT merupakan segitiga sama kaki, sehingga AP = CP = 5 cm.
$PT^2 = AT^2 - AP^2$
$= 13^2 - 5^2$
$= 169 - 25$
$= 144$
$PT = \sqrt{144}$
$= 12\ cm$
$\dfrac12.AC.PT = \dfrac12.CT.AE$
$AC.PT = CT.AE$
$AE = \dfrac{AC.PT}{CT}$
$= \dfrac{10.12}{13}$
$= \dfrac{120}{13}$
$= 9\dfrac{3}{13}\ cm$
jawab: C.
26. Diketahui rusuk kubus ABCD.EFGH adalah $a$ satuan, tangen sudut antara garis AH dan bidang BDHF adalah . . . .
$A.\ \dfrac13$
$B.\ \dfrac12\sqrt{3}$
$C.\ \dfrac13\sqrt{3}$
$D.\ 1$
$E.\ \sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2016 MtkIPA]
$A.\ \dfrac13$
$B.\ \dfrac12\sqrt{3}$
$C.\ \dfrac13\sqrt{3}$
$D.\ 1$
$E.\ \sqrt{3}$
[Soal dan Pembahasan Dimensi Tiga UN 2016 MtkIPA]
Perhatikan gambar !
Proyeksi titik A terhadap bidang BDHF adalah titik P, sehingga proyeksi garis AH terhadap bidang BDHF adalah garis HP.
$AC = a\sqrt{2}$ → Diagonal sisi
$AP = DP = \dfrac12AC = \dfrac12a\sqrt{2}$
$HP^2 = HD^2 + DP^2$
$= a^2 + \left(\dfrac12a\sqrt{2}\right)^2$
$= a^2 + \dfrac12a^2$
$= \dfrac32a^2$
$HP = \sqrt{\dfrac32a^2}$
$= \dfrac12a\sqrt{6}$
$tan\ \alpha = \dfrac{AP}{HP}$
$= \dfrac{\dfrac12a\sqrt{2}}{\dfrac12a\sqrt{6}}$
$= \dfrac{\sqrt{2}}{\sqrt{6}}$
$= \dfrac16\sqrt{12}$
$= \dfrac13\sqrt{3}$
jawab: C.
Proyeksi titik A terhadap bidang BDHF adalah titik P, sehingga proyeksi garis AH terhadap bidang BDHF adalah garis HP.
$AC = a\sqrt{2}$ → Diagonal sisi
$AP = DP = \dfrac12AC = \dfrac12a\sqrt{2}$
$HP^2 = HD^2 + DP^2$
$= a^2 + \left(\dfrac12a\sqrt{2}\right)^2$
$= a^2 + \dfrac12a^2$
$= \dfrac32a^2$
$HP = \sqrt{\dfrac32a^2}$
$= \dfrac12a\sqrt{6}$
$tan\ \alpha = \dfrac{AP}{HP}$
$= \dfrac{\dfrac12a\sqrt{2}}{\dfrac12a\sqrt{6}}$
$= \dfrac{\sqrt{2}}{\sqrt{6}}$
$= \dfrac16\sqrt{12}$
$= \dfrac13\sqrt{3}$
jawab: C.
27. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. Titik N tengah-tengah AE. Jarak titik H ke BN adalah . . . .
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 2\sqrt{5}\ cm$
$D.\ \dfrac25\sqrt{30}\ cm$
$E.\ \dfrac45\sqrt{30}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2015 MtkIPA]
$A.\ 2\sqrt{2}\ cm$
$B.\ 2\sqrt{3}\ cm$
$C.\ 2\sqrt{5}\ cm$
$D.\ \dfrac25\sqrt{30}\ cm$
$E.\ \dfrac45\sqrt{30}\ cm$
[Soal dan Pembahasan Dimensi Tiga UN 2015 MtkIPA]
Perhatikan gambar !
$BN^2 = AB^2 + AN^2$
$= 4^2 + 2^2$
$= 16 + 4$
$= 20$
$BN = \sqrt{20}$
$= 2\sqrt{5}$
$HN = BN = 2\sqrt{5}$
$BH = 4\sqrt{3}$ → Diagonal ruang.
$NP = \dfrac12AC$
$= \dfrac12.4\sqrt{2}$
$= 2\sqrt{2}$
Prinsip luas segitiga:
$NP.BH = BN.HQ$
$HQ = \dfrac{NP.BH}{BN}$
$= \dfrac{2\sqrt{2}.4\sqrt{3}}{2\sqrt{5}}$
$= \dfrac{4\sqrt{6}}{\sqrt{5}}$
$= \dfrac45\sqrt{30}$
jawab: E.
$BN^2 = AB^2 + AN^2$
$= 4^2 + 2^2$
$= 16 + 4$
$= 20$
$BN = \sqrt{20}$
$= 2\sqrt{5}$
$HN = BN = 2\sqrt{5}$
$BH = 4\sqrt{3}$ → Diagonal ruang.
$NP = \dfrac12AC$
$= \dfrac12.4\sqrt{2}$
$= 2\sqrt{2}$
Prinsip luas segitiga:
$NP.BH = BN.HQ$
$HQ = \dfrac{NP.BH}{BN}$
$= \dfrac{2\sqrt{2}.4\sqrt{3}}{2\sqrt{5}}$
$= \dfrac{4\sqrt{6}}{\sqrt{5}}$
$= \dfrac45\sqrt{30}$
jawab: E.
28. Kubus ABCD.EFGH dengan rusuk 12 cm, sinus sudut antara bidang ACF dengan bidang ACH adalah . . . .
$A.\ \dfrac13$
$B.\ \dfrac12\sqrt{2}$
$C.\ \dfrac23\sqrt{2}$
$D.\ \sqrt{2}$
$E.\ 2\sqrt{2}$
[Soal dan Pembahasan Dimensi Tiga UN 2015 MtkIPA]
$A.\ \dfrac13$
$B.\ \dfrac12\sqrt{2}$
$C.\ \dfrac23\sqrt{2}$
$D.\ \sqrt{2}$
$E.\ 2\sqrt{2}$
[Soal dan Pembahasan Dimensi Tiga UN 2015 MtkIPA]
Perhatikan gambar !
$BD = 12\sqrt{2}$ → Diagonal sisi.
$BP = \dfrac12BD$
$= \dfrac12.12\sqrt{2}$
$= 6\sqrt{2}\ cm$
$FP^2 = BP^2 + BF^2$
$= (6\sqrt{2})^2 + 12^2$
$= 72 + 144$
$= 216$
$= 36.6$
$FP = \sqrt{36.6}$
$= 6\sqrt{6}\ cm$
$HP = FP = 6\sqrt{6}$
$FH = 12\sqrt{2}$ → Diagonal sisi.
Prinsip luas segitiga:
$\dfrac12.FH.PQ = \dfrac12.FP.HP.sin\ \alpha$
$FH.PQ = FP.HP.sin\ \alpha$
$sin\ \alpha = \dfrac{FH.PQ}{FP.HP}$
$= \dfrac{12\sqrt{2}.12}{6\sqrt{6}.6\sqrt{6}}$
$= \dfrac23\sqrt{2}$
jawab: C.
$BD = 12\sqrt{2}$ → Diagonal sisi.
$BP = \dfrac12BD$
$= \dfrac12.12\sqrt{2}$
$= 6\sqrt{2}\ cm$
$FP^2 = BP^2 + BF^2$
$= (6\sqrt{2})^2 + 12^2$
$= 72 + 144$
$= 216$
$= 36.6$
$FP = \sqrt{36.6}$
$= 6\sqrt{6}\ cm$
$HP = FP = 6\sqrt{6}$
$FH = 12\sqrt{2}$ → Diagonal sisi.
Prinsip luas segitiga:
$\dfrac12.FH.PQ = \dfrac12.FP.HP.sin\ \alpha$
$FH.PQ = FP.HP.sin\ \alpha$
$sin\ \alpha = \dfrac{FH.PQ}{FP.HP}$
$= \dfrac{12\sqrt{2}.12}{6\sqrt{6}.6\sqrt{6}}$
$= \dfrac23\sqrt{2}$
jawab: C.
29. Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jarak titik C ke bidang BDG adalah . . . .
$A.\ \dfrac43\sqrt{3}$
$B.\ \dfrac34\sqrt{3}$
$C.\ \dfrac43\sqrt{2}$
$D.\ \dfrac34\sqrt{2}$
$E,\ \dfrac83$
[Soal dan Pembahasan Dimensi Tiga UM UGM 2017 Mtk IPA]
$A.\ \dfrac43\sqrt{3}$
$B.\ \dfrac34\sqrt{3}$
$C.\ \dfrac43\sqrt{2}$
$D.\ \dfrac34\sqrt{2}$
$E,\ \dfrac83$
[Soal dan Pembahasan Dimensi Tiga UM UGM 2017 Mtk IPA]
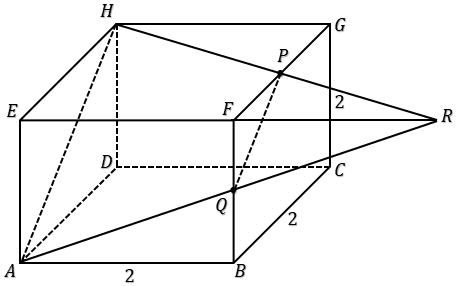
30. Pada kubus ABCD.EFGH, P adalah titik tengah FG dan titik Q adalah titik tengah FB. Perpanjangan HP dan AQ berpotongan di perpanjangan EF di titik R. Jika panjang rusuk kubus adalah 2, maka perbandingan volume EAH.FQP : volume ABCD.EFGH adalah . . . .
A. 1 : 4
B. 1 : 8
C. 3 : 8
D. 7 : 24
E. 8 : 25
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2015 MtkIPA]
A. 1 : 4
B. 1 : 8
C. 3 : 8
D. 7 : 24
E. 8 : 25
[Soal dan Pembahasan Dimensi Tiga SBMPTN 2015 MtkIPA]
$\dfrac{FQ}{AE} = \dfrac{FR}{ER}$
$\dfrac{1}{2} = \dfrac{FR}{(FR + 2)}$
$FR + 2 = 2FR$
$FR = 2$
$ER = 4$
Volume R.EAH:
$V_1 = \dfrac13.\dfrac12.EA.EH.ER$
$= \dfrac16.2.2.4$
$= \dfrac83$
Volume R.FQP:
$V_2 = \dfrac13.\dfrac12.FP.FQ.FR$
$= \dfrac16.1.1.2$
$= \dfrac13$
$Volume\ EAH.FQP = \dfrac83 - \dfrac13 = \dfrac73$
$Volume\ ABCD.EFGH = 2.2.2 = 8$
$\dfrac{Volume\ EAH.FQP}{Volume\ ABCD.EFGH} = \dfrac{\dfrac73}{8}$
$= \dfrac{7}{24}$
$= 7 : 24$
jawab: D.
$\dfrac{1}{2} = \dfrac{FR}{(FR + 2)}$
$FR + 2 = 2FR$
$FR = 2$
$ER = 4$
Volume R.EAH:
$V_1 = \dfrac13.\dfrac12.EA.EH.ER$
$= \dfrac16.2.2.4$
$= \dfrac83$
Volume R.FQP:
$V_2 = \dfrac13.\dfrac12.FP.FQ.FR$
$= \dfrac16.1.1.2$
$= \dfrac13$
$Volume\ EAH.FQP = \dfrac83 - \dfrac13 = \dfrac73$
$Volume\ ABCD.EFGH = 2.2.2 = 8$
$\dfrac{Volume\ EAH.FQP}{Volume\ ABCD.EFGH} = \dfrac{\dfrac73}{8}$
$= \dfrac{7}{24}$
$= 7 : 24$
jawab: D.
Demikianlah soal dan pembahasan dimensi tiga, semoga bermanfaat. Selamat Belajar !
Disusun oleh:
Joslin Sibarani
Alumni Teknik Sipil ITB
www.maretong.com























jazaakallah khaeran katsiira
ReplyDeleteKak mau tanya kumis ABCD.EFGH dengan panjang rusuk 6 cm.Q dan P adalah titik tengah HG dan FG.Jika Alfa adalah sudut yang dibentuk bidang BDPQ dengan bidang ABCD maka nilai sin Alfa adalah
ReplyDeleteGatau anjing
DeleteOk pak
ReplyDeletemaretong = marita?
ReplyDelete