Soal dan Pembahasan Bangun Datar Segitiga merupakan pembahasan soal-soal khusus tentang segitiga dengan segala bentuk persoalannya. Pada pembahasan ini, penekanan adalah cara menghitung sudut dalam dan sudut luar segitiga serta luas dan keliling segitiga. Sebelum berbicara tentang soal dan pembahasan, sebaiknya kita lakukan ulasan singkat tentang materi ini supaya adik-adik yang sudah agak lupa tentang segitiga bisa mengingat kembali hal-hal mengenai materi segitiga ini.
Garis tinggi adalah garis lurus yang ditarik dari titik sudut segitiga dan tegak lurus sisi yang di depannya.
CE disebut garis tinggi.
2. Garis Bagi.
Garis bagi adalah garis lurus yang ditarik dari titik sudut segitiga dan membagi dua sudut tersebut sama besar.
AE disebut garis bagi.
3. Garis Sumbu.
Garis sumbu adalah garis lurus yang mememotong titik tengah sisi suatu segitiga secara tegak lurus.
DE disebut garis sumbu.
4. Garis Berat.
Garis berat adalah garis lurus yang ditarik dari titik sudut suatu segitiga dan membagi dua sisi yang di depannya sama panjang.
CD disebut garis berat.
AB disebut alas
CE disebut tinggi
$Luas = \dfrac{1}{2}\ \times\ alas\ \times\ tinggi$
$Jika\ alas = a\ dan\ tinggi = t,\ maka:$
$Luas = \dfrac{1}{2}at$
$Keliling = AB + BC + AC$
Note:
Panjang salah satu sisi segitiga harus lebih kecil dari jumlah kedua sisi yang lain.
$AB < BC + AC$
$BC < AB + AC$
$AC < AB + BC$
Sudut terbesar selalu menghadap sisi terpanjang. Sudut terkecil selalu menghadap sisi terpendek. Sudut yang sedang menghadap sisi yang sedang.
Perhatikan gambar !
$\angle ABD\ dan\ \angle BCE$ adalah sudut luar segitiga ABC.
$\angle ABD + \angle ABC = 180^o$ . . . . (1)
$\angle BAC + \angle ACB + \angle ABC = 180^o$ . . . . (2)
Dari persamaan (1) dan (2)
$\angle ABD + \angle ABC = \angle BAC + \angle ACB + \angle ABC$
$\angle ABD = \angle BAC + \angle ACB$
Dengan cara yang sama,
$\angle BCE = \angle BAC + \angle ABC$
Demikianlah soal dan pembahasan bangun datar segitiga. Selamat belajar !
SHARE THIS POST
wwww.maretong.com
Daftar isi
Pengertian dan Jenis-jenis Segitiga
Bangun datar segitiga adalah bangun dua dimensi yang dibatasi oleh tiga buah sisi. Segitiga bisa dibedakan berdasarkan panjang sisi-sisinya dan besar sudut-sudutnya.$\bullet$ Jika ditinjau dari panjang sisi-sisinya, bangun datar segitiga dibagi atas tiga bagian, yaitu:
1. Segitiga sembarang.
Segitiga sembarang memiliki panjang sisi-sisi yang berbeda.
$AB ≠ BC ≠ AC$
$\angle A + \angle B + \angle C = 180^o$
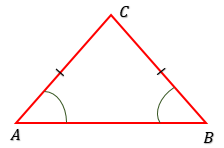
2. Segitiga sama kaki.
Segitiga sama kaki adalah segitiga yang memiliki dua buah sisi sama panjang dan dua buah sudut sama besar.
$AC = BC$
$\angle A = \angle B$
$\angle A + \angle B + \angle C = 180^o$
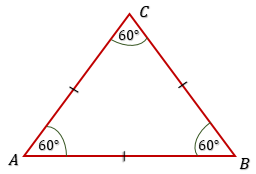
3. Segitiga sama sisi.
Segitiga sama sisi adalah segitiga yang ketiga sisi-sisinya sama panjang, dan ketiga sudutnya sama besar yang besarnya adalah $60^o$.
$AB = BC = AC$
$\angle A = \angle B = \angle C = 60^o$
1. Segitiga sembarang.
Segitiga sembarang memiliki panjang sisi-sisi yang berbeda.
$AB ≠ BC ≠ AC$
$\angle A + \angle B + \angle C = 180^o$
2. Segitiga sama kaki.
Segitiga sama kaki adalah segitiga yang memiliki dua buah sisi sama panjang dan dua buah sudut sama besar.
$AC = BC$
$\angle A = \angle B$
$\angle A + \angle B + \angle C = 180^o$
3. Segitiga sama sisi.
Segitiga sama sisi adalah segitiga yang ketiga sisi-sisinya sama panjang, dan ketiga sudutnya sama besar yang besarnya adalah $60^o$.
$AB = BC = AC$
$\angle A = \angle B = \angle C = 60^o$
$\bullet$ Jika ditinjau dari besar sudutnya, segitiga dibagi atas tiga bagian, yaitu:
1. Segitiga lancip.
Segitiga lancip adalah segitiga yang ketiga sudutnya lebih kecil dari $90^o$.
$\angle A < 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$AB^2 < BC^2 + AC^2$
2. Segitiga siku-siku.
Segitiga siku-siku adalah segitiga yang salah satu sudutnya adalah $90^o$ dan kedua sudut yang lain besarnya lebih kecil dari $90^o$.
$\angle A = 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$BC^2 = AB^2 + AC^2$
3. Segitiga tumpul.
Segitiga tumpul adalah segitiga yang salah satu sudutnya lebih besar dari $90^o$ dan kedua sudut yang lain besarnya lebih kecil dari $90^o$.
$\angle A > 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$BC^2 > AB^2 + AC^2$
1. Segitiga lancip.
Segitiga lancip adalah segitiga yang ketiga sudutnya lebih kecil dari $90^o$.
$\angle A < 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$AB^2 < BC^2 + AC^2$
2. Segitiga siku-siku.
Segitiga siku-siku adalah segitiga yang salah satu sudutnya adalah $90^o$ dan kedua sudut yang lain besarnya lebih kecil dari $90^o$.
$\angle A = 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$BC^2 = AB^2 + AC^2$
3. Segitiga tumpul.
Segitiga tumpul adalah segitiga yang salah satu sudutnya lebih besar dari $90^o$ dan kedua sudut yang lain besarnya lebih kecil dari $90^o$.
$\angle A > 90^o$
$\angle B < 90^o$
$\angle C < 90^o$
$BC^2 > AB^2 + AC^2$
Garis-garis Istimewa Pada Segitiga
1. Garis Tinggi.Garis tinggi adalah garis lurus yang ditarik dari titik sudut segitiga dan tegak lurus sisi yang di depannya.
CE disebut garis tinggi.
2. Garis Bagi.
Garis bagi adalah garis lurus yang ditarik dari titik sudut segitiga dan membagi dua sudut tersebut sama besar.
AE disebut garis bagi.
3. Garis Sumbu.
Garis sumbu adalah garis lurus yang mememotong titik tengah sisi suatu segitiga secara tegak lurus.
DE disebut garis sumbu.
4. Garis Berat.
Garis berat adalah garis lurus yang ditarik dari titik sudut suatu segitiga dan membagi dua sisi yang di depannya sama panjang.
CD disebut garis berat.
Rumus Luas dan Rumus Keliling Segitiga
AB disebut alas
CE disebut tinggi
$Luas = \dfrac{1}{2}\ \times\ alas\ \times\ tinggi$
$Jika\ alas = a\ dan\ tinggi = t,\ maka:$
$Luas = \dfrac{1}{2}at$
$Keliling = AB + BC + AC$
Note:
Panjang salah satu sisi segitiga harus lebih kecil dari jumlah kedua sisi yang lain.
$AB < BC + AC$
$BC < AB + AC$
$AC < AB + BC$
Sudut terbesar selalu menghadap sisi terpanjang. Sudut terkecil selalu menghadap sisi terpendek. Sudut yang sedang menghadap sisi yang sedang.
Rumus Sudut Luar Segitiga
Besar sudut luar suatu segitiga sama dengan besar sudut dalam yang tidak berpelurus dengan sudut luar tersebut.Perhatikan gambar !
$\angle ABD\ dan\ \angle BCE$ adalah sudut luar segitiga ABC.
$\angle ABD + \angle ABC = 180^o$ . . . . (1)
$\angle BAC + \angle ACB + \angle ABC = 180^o$ . . . . (2)
Dari persamaan (1) dan (2)
$\angle ABD + \angle ABC = \angle BAC + \angle ACB + \angle ABC$
$\angle ABD = \angle BAC + \angle ACB$
Dengan cara yang sama,
$\angle BCE = \angle BAC + \angle ABC$
Contoh Soal dan Pembahasan Bangun Datar Segitiga
1. Diketahui sudut-sudut sebuah segitiga adalah $60^o$ dan $80^o$, maka besar sudut yang lain adalah . . . .
$A.\ 30^o$
$B.\ 40^o$
$C.\ 50^o$
$A.\ 60^o$
$A.\ 30^o$
$B.\ 40^o$
$C.\ 50^o$
$A.\ 60^o$
Sudut dalam segitiga besarnya adalah $180^o$. Misalkan besar sudut yang lain adalah $x$, maka:
$\begin{align*}
60^o + 80^o + x &= 180^o\\
140^o + x &= 180^o\\
x &= 180^o - 140^o\\
x &= 40^o → B.
\end{align*}$
$\begin{align*}
60^o + 80^o + x &= 180^o\\
140^o + x &= 180^o\\
x &= 180^o - 140^o\\
x &= 40^o → B.
\end{align*}$
$\begin{align*}
\angle A + \angle B + \angle C &= 180^o\\
60^o + 3x^o + 5x^o &= 180^o\\
60^o + 8x^o &= 180^o\\
8x^o &= 180^o - 60^o\\
8x^o &= 120^o\\
x &= 15\\
\angle B &= 3x^o\\
&= 3.15^o\\
&= 45^o → A.
\end{align*}$
\angle A + \angle B + \angle C &= 180^o\\
60^o + 3x^o + 5x^o &= 180^o\\
60^o + 8x^o &= 180^o\\
8x^o &= 180^o - 60^o\\
8x^o &= 120^o\\
x &= 15\\
\angle B &= 3x^o\\
&= 3.15^o\\
&= 45^o → A.
\end{align*}$
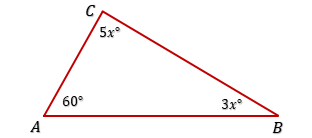
3. Besar sudut-sudut sebuah segitiga adalah $2x^o$, $(x + 30)^o$, dan $(2x + 50)^o$. Nilai $x$ adalah . . . .
A. 5
B. 10
C. 15
D. 20
A. 5
B. 10
C. 15
D. 20
$\begin{align*}
2x^o + (x + 30)^o + (2x + 50)^o &= 180^o\\
2x + x + 30 + 2x + 50 &= 180\\
5x + 80 &= 180\\
5x &= 180 - 80\\
5x &= 100\\
x &= 20 → D.
\end{align*}$
2x^o + (x + 30)^o + (2x + 50)^o &= 180^o\\
2x + x + 30 + 2x + 50 &= 180\\
5x + 80 &= 180\\
5x &= 180 - 80\\
5x &= 100\\
x &= 20 → D.
\end{align*}$
4. Diketahui segitiga sama kaki ABC, AC = BC. Jika besar $\angle ABC = 50^o$, maka besar $\angle ACB =$ . . . .
$A.\ 80^o$
$B.\ 100^o$
$C.\ 120^o$
$D.\ 125^o$
$A.\ 80^o$
$B.\ 100^o$
$C.\ 120^o$
$D.\ 125^o$
5. Perhatikan Gambar !
Jika besar $\angle A = 40^o$, maka besar $\angle ACB$ adalah . . . .
$A.\ 10^o$
$B.\ 20^o$
$C.\ 30^o$
$D.\ 50^o$
Jika besar $\angle A = 40^o$, maka besar $\angle ACB$ adalah . . . .
$A.\ 10^o$
$B.\ 20^o$
$C.\ 30^o$
$D.\ 50^o$
$\begin{align*}
\angle A = \angle ADC &= 40^o\\
\angle A + \angle ADC + \angle ACD &= 180^o\\
40^o + 40^o + \angle ACD &= 180^o\\
80^o + \angle ACD &= 180^o\\
\angle ACD &= 180^o - 80^o\\
\angle ACD &= 100^o\\
\angle ADC + \angle BDC &= 180^o\\
40^o + \angle BDC &= 180^o\\
\angle BDC &= 180^o - 40^o\\
\angle BDC &= 140^o\\
\end{align*}$
$Karena\ segitiga\ BCD\ sama\ kaki:$
$\begin{align*}
maka\ \angle B &= \angle BCD\\
Misalkan\ sudut\ B &= n\\
\angle B + \angle BDC + \angle BCD &= 180^o\\
n + 140^o + n &= 180^o\\
2n &= 180^o - 140^o\\
2n &= 40^o\\
n &= 20^o → B.
\end{align*}$
\angle A = \angle ADC &= 40^o\\
\angle A + \angle ADC + \angle ACD &= 180^o\\
40^o + 40^o + \angle ACD &= 180^o\\
80^o + \angle ACD &= 180^o\\
\angle ACD &= 180^o - 80^o\\
\angle ACD &= 100^o\\
\angle ADC + \angle BDC &= 180^o\\
40^o + \angle BDC &= 180^o\\
\angle BDC &= 180^o - 40^o\\
\angle BDC &= 140^o\\
\end{align*}$
$Karena\ segitiga\ BCD\ sama\ kaki:$
$\begin{align*}
maka\ \angle B &= \angle BCD\\
Misalkan\ sudut\ B &= n\\
\angle B + \angle BDC + \angle BCD &= 180^o\\
n + 140^o + n &= 180^o\\
2n &= 180^o - 140^o\\
2n &= 40^o\\
n &= 20^o → B.
\end{align*}$
6. Segitiga PQR adalah segitiga sama kaki dengan PR = QR dan $\angle P\ :\ \angle R = 3\ :\ 4$. Besar $\angle Q$ adalah . . . .
$A.\ 36^o$
$B.\ 48^o$
$C.\ 54^o$
$D.\ 72^o$
$A.\ 36^o$
$B.\ 48^o$
$C.\ 54^o$
$D.\ 72^o$
7. Segitiga KLM adalah segitiga sama kaki, dimana KL = LM. Jika kililing segitiga KLM = 60 cm dan panjang KM = 30 cm, maka panjang KL = . . . .
A. 5 cm
B. 10 cm
C. 15 cm
D. 20 cm
A. 5 cm
B. 10 cm
C. 15 cm
D. 20 cm
$Misalkan\ panjang\ KL = LM = p$
$\begin{align*}
Keliling &= KL + LM + KM\\
60 &= p + p + 30\\
60 &= 2p + 30\\
60 - 30 &= 2p\\
30 &= 2p\\
15 &= p\\
Panjang\ KL &= p\\
&= 15\ cm → C.
\end{align*}$
$\begin{align*}
Keliling &= KL + LM + KM\\
60 &= p + p + 30\\
60 &= 2p + 30\\
60 - 30 &= 2p\\
30 &= 2p\\
15 &= p\\
Panjang\ KL &= p\\
&= 15\ cm → C.
\end{align*}$
8. Diketahui Keliling $\Delta PQR = 180\ cm$. Jika $PQ\ :\ QR\ :\ PR = 2\ :\ 3\ :\ 4$, maka panjang $QR =$ . . . .
$A.\ 40\ cm$
$B.\ 50\ cm$
$C.\ 60\ cm$
$D.\ 80\ cm$
$A.\ 40\ cm$
$B.\ 50\ cm$
$C.\ 60\ cm$
$D.\ 80\ cm$
$\begin{align*}
Misalkan:\\
PQ &= 2n\\
QR &= 3n\\
PR &= 4n\\
Keliling &= PQ + QR + PR\\
180 &= 2n + 3n + 4n\\
180 &= 9n\\
20 &= n\\
QR &= 3n\\
&= 3.20\\
&= 60\ cm → C.
\end{align*}$
Misalkan:\\
PQ &= 2n\\
QR &= 3n\\
PR &= 4n\\
Keliling &= PQ + QR + PR\\
180 &= 2n + 3n + 4n\\
180 &= 9n\\
20 &= n\\
QR &= 3n\\
&= 3.20\\
&= 60\ cm → C.
\end{align*}$
9. Panjang alas suatu segitiga = 16 cm, dan tingginya = 8 cm. Luas segitiga tersebut adalah . . . .
$A.\ 64\ cm^2$
$B.\ 48\ cm^2$
$C.\ 42\ cm^2$
$D.\ 36\ cm^2$
$A.\ 64\ cm^2$
$B.\ 48\ cm^2$
$C.\ 42\ cm^2$
$D.\ 36\ cm^2$
$Luas = \dfrac{1}{2}\ \times\ alas\ \times\ tinggi$
$Luas = \dfrac{1}{2}\ \times\ 16\ \times\ 8$
$Luas = 64\ cm^2$ → A.
$Luas = \dfrac{1}{2}\ \times\ 16\ \times\ 8$
$Luas = 64\ cm^2$ → A.
10. Perhatikan gambar !
Luas segitiga pada gambar di atas adalah . . . .
$A.\ 18\ cm^2$
$B.\ 24\ cm^2$
$C.\ 28\ cm^2$
$D.\ 32\ cm^2$
Luas segitiga pada gambar di atas adalah . . . .
$A.\ 18\ cm^2$
$B.\ 24\ cm^2$
$C.\ 28\ cm^2$
$D.\ 32\ cm^2$
$\begin{align*}
BC^2 &= AB^2 + AC^2\\
10^2 &= AB^2 + 6^2\\
100 &= AB^2 + 36\\
100 - 36 &= AB^2\\
64 &= AB^2\\
AB &= \sqrt{64}\\
AB &= 8\ cm\\
alas = AB &= 8\ cm\\
tinggi = AC &= 6\ cm\\
L &= \dfrac{1}{2}.8.6\\
&= 4.6\\
&= 24\ cm^2 → B.
\end{align*}$
Catatan:
Alas dan tinggi selalu saling tegak lurus.
BC^2 &= AB^2 + AC^2\\
10^2 &= AB^2 + 6^2\\
100 &= AB^2 + 36\\
100 - 36 &= AB^2\\
64 &= AB^2\\
AB &= \sqrt{64}\\
AB &= 8\ cm\\
alas = AB &= 8\ cm\\
tinggi = AC &= 6\ cm\\
L &= \dfrac{1}{2}.8.6\\
&= 4.6\\
&= 24\ cm^2 → B.
\end{align*}$
Catatan:
Alas dan tinggi selalu saling tegak lurus.
11. Perhatikan gambar !
Luas segitiga di atas adalah . . . .
$A.\ 24\ cm^2$
$B.\ 32\ cm^2$
$C.\ 36\ cm^2$
$D.\ 48\ cm^2$
Luas segitiga di atas adalah . . . .
$A.\ 24\ cm^2$
$B.\ 32\ cm^2$
$C.\ 36\ cm^2$
$D.\ 48\ cm^2$
AB → alas.
CD → tinggi.
$\begin{align*}
AC^2 &= AD^2 + CD^2\\
10^2 &= 6^2 + CD^2\\
100 &= 36 + CD^2\\
100 - 36 &= CD^2\\
64 &= CD^2\\
CD &= \sqrt{64}\\
CD &= 8\ cm\\
Luas &= \dfrac{1}{2}.AB.CD\\
&= \dfrac{1}{2}.12.8\\
&= 6.8\\
&= 48\ cm^2 → D.
\end{align*}$
CD → tinggi.
$\begin{align*}
AC^2 &= AD^2 + CD^2\\
10^2 &= 6^2 + CD^2\\
100 &= 36 + CD^2\\
100 - 36 &= CD^2\\
64 &= CD^2\\
CD &= \sqrt{64}\\
CD &= 8\ cm\\
Luas &= \dfrac{1}{2}.AB.CD\\
&= \dfrac{1}{2}.12.8\\
&= 6.8\\
&= 48\ cm^2 → D.
\end{align*}$
12. $\angle ABC\ siku-siku\ di\ A,$ ditarik garis k dari titik C ke titik tengah AB. Garis k dinamakan . . . .
A. Garis bagi
B. Garis berat
C. Garis tinggi
D. Garis sumbu
[Soal UN]
A. Garis bagi
B. Garis berat
C. Garis tinggi
D. Garis sumbu
[Soal UN]
Garis yang ditarik dari titik sudut ke titik tengah sisi yang dihadapannya adalah garis berat. → B.
13. Sebuah segitiga dapat dibentuk dari tiga buah garis berukuran seperti dibawah. Tiga buah garis yang tidak mungkin membentuk sebuah segitiga adalah . . . .
A. 5 cm, 6 cm, dan 8 cm
B. 11 cm, 7 cm, dan 15 cm
C. 3 cm, 4 cm, dan 5 cm
D. 6 cm, 4 cm, dan 11 cm
A. 5 cm, 6 cm, dan 8 cm
B. 11 cm, 7 cm, dan 15 cm
C. 3 cm, 4 cm, dan 5 cm
D. 6 cm, 4 cm, dan 11 cm
Panjang salah satu sisi tidak boleh lebih atau sama dengan jumlah panjang dua sisi yang lain. Lihat pilihan D !
11 cm ≥ 6 cm + 4 cm
Salah satu sisi lebih panjang dari jumlah dua sisi yang lain, sehingga tidak mungkin membentuk segitiga.
Jawab: D.
11 cm ≥ 6 cm + 4 cm
Salah satu sisi lebih panjang dari jumlah dua sisi yang lain, sehingga tidak mungkin membentuk segitiga.
Jawab: D.
$\begin{align*}
\angle ADB &= 180^o - 108^o\\
\angle ADB &= 72^o\\
\angle ADB + \angle BAD + \angle ABD &= 180^o . . . . (1)\\
\angle ABD + \angle CBD &= 180^o . . . . (2)\\
Dari\ persamaan\ (1)\ dan\ (2)\\
\angle ADB + \angle BAD + \angle ABD &= \angle ABD + \angle CBD\\
\angle ADB + \angle BAD &= \angle CBD\\
48^o + 72^o &= (2x - 10)^o\\
120^o &= (2x - 10)^o\\
120 &= 2x - 10\\
120 + 10 &= 2x\\
130 &= 2x\\
65 &= x → D.
\end{align*}$
\angle ADB &= 180^o - 108^o\\
\angle ADB &= 72^o\\
\angle ADB + \angle BAD + \angle ABD &= 180^o . . . . (1)\\
\angle ABD + \angle CBD &= 180^o . . . . (2)\\
Dari\ persamaan\ (1)\ dan\ (2)\\
\angle ADB + \angle BAD + \angle ABD &= \angle ABD + \angle CBD\\
\angle ADB + \angle BAD &= \angle CBD\\
48^o + 72^o &= (2x - 10)^o\\
120^o &= (2x - 10)^o\\
120 &= 2x - 10\\
120 + 10 &= 2x\\
130 &= 2x\\
65 &= x → D.
\end{align*}$
15. Perhatikan gambar bangun yang terdiri dari jajargenjang dan segitiga siku-siku.
Keliling bangun tersebut adalah . . . .
A. 105 cm
B. 120 cm
C. 123 cm
D. 156 cm
[Soal UN 2018]
Keliling bangun tersebut adalah . . . .
A. 105 cm
B. 120 cm
C. 123 cm
D. 156 cm
[Soal UN 2018]
$\begin{align*}
BC = CD = AE &= 15\ cm\\
AC^2 &= AB^2 - BC^2\\
&= 39^2 - 15^2\\
&= 1521 - 225\\
&= 1296\\
AC &= \sqrt{1296}\\
AC &= 36\ cm\\
AC = DE &= 36\ cm\\
Keliling &= AB + BC + CD + DE + AE\\
&= 39 + 15 + 15 + 36 + 15\\
&= 120\ cm → B.
\end{align*}$
BC = CD = AE &= 15\ cm\\
AC^2 &= AB^2 - BC^2\\
&= 39^2 - 15^2\\
&= 1521 - 225\\
&= 1296\\
AC &= \sqrt{1296}\\
AC &= 36\ cm\\
AC = DE &= 36\ cm\\
Keliling &= AB + BC + CD + DE + AE\\
&= 39 + 15 + 15 + 36 + 15\\
&= 120\ cm → B.
\end{align*}$
16. Seorang pengamat berada di atas mercusuar yang tingginya 12 meter. Ia melihat kapal A dan kapal B yang berlayar di laut. Jarak pengamat dengan kapal A dan kapal B berturut-turut 20 meter dan 13 meter. Posisi kapal A, kapal B, dan kaki mercusuar terletak segaris. Jarak kapal A dan kapal B adalah . . . .
A. 7 meter
B. 11 meter
C. 12 meter
D. 15 meter
[Soal UN 2018]
A. 7 meter
B. 11 meter
C. 12 meter
D. 15 meter
[Soal UN 2018]
17. Diketahui keliling suatu segitiga 52 cm, dan panjang salah satu sisinya adalah 20 cm. Jika perbandingan sisi kedua dan ketiga adalah 1 : 3, maka panjang sisi-sisi segitiga tersebut adalah . . . .
A. 6 cm, 20 cm, dan 30 cm
B. 8 cm, 20 cm, dan 24 cm
C. 10 cm, 20 cm, dan 22 cm
D. 12 cm, 20 cm, dan 20 cm
A. 6 cm, 20 cm, dan 30 cm
B. 8 cm, 20 cm, dan 24 cm
C. 10 cm, 20 cm, dan 22 cm
D. 12 cm, 20 cm, dan 20 cm
Misalkan segitiga yang dimaksud adalah segitiga ABC.
$\begin{align*}
K = 52\ dan\ AB &= 20\ cm\\
BC\ :\ AC &= 1\ :\ 3\\
Misalkan\ BC &= n\ dan\ AC = 3n\\
K &= AB + BC + AC\\
52 &= 20 + n + 3n\\
52 - 20 &= 4n\\
32 &= 4n\\
8 &= n\\
BC = n &= 8\ cm\\
AC = 3n = 3.8 &= 24\ cm\\
\end{align*}$
Maka sisi-sisi segitiga tersebut adalah:
8 cm, 20 cm, dan 24 cm. → B.
$\begin{align*}
K = 52\ dan\ AB &= 20\ cm\\
BC\ :\ AC &= 1\ :\ 3\\
Misalkan\ BC &= n\ dan\ AC = 3n\\
K &= AB + BC + AC\\
52 &= 20 + n + 3n\\
52 - 20 &= 4n\\
32 &= 4n\\
8 &= n\\
BC = n &= 8\ cm\\
AC = 3n = 3.8 &= 24\ cm\\
\end{align*}$
Maka sisi-sisi segitiga tersebut adalah:
8 cm, 20 cm, dan 24 cm. → B.
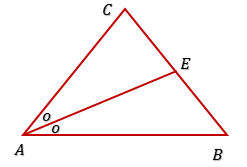
18. Perhatikan gambar !
Besar $\angle BAC$ adalah . . . .
$A.\ 30^o$
$B.\ 40^o$
$C.\ 50^o$
$D.\ 60^o$
Besar $\angle BAC$ adalah . . . .
$A.\ 30^o$
$B.\ 40^o$
$C.\ 50^o$
$D.\ 60^o$
$\begin{align*}
\angle BAC &= 180^o - 5x^o\\
\angle BCE &= \angle BAC + \angle ABC\\
(3x - 20)^o &= 180^o - 5x^o + 40^o\\
3x - 20 &= 180 - 5x + 40\\
3x + 5x &= 180 + 40 + 20\\
8x &= 240\\
x &= 30\\
\angle BAC &= 180^o - 5.30^o\\
&= 180^o - 150^o\\
&= 30^o → A.
\end{align*}$
\angle BAC &= 180^o - 5x^o\\
\angle BCE &= \angle BAC + \angle ABC\\
(3x - 20)^o &= 180^o - 5x^o + 40^o\\
3x - 20 &= 180 - 5x + 40\\
3x + 5x &= 180 + 40 + 20\\
8x &= 240\\
x &= 30\\
\angle BAC &= 180^o - 5.30^o\\
&= 180^o - 150^o\\
&= 30^o → A.
\end{align*}$
19. Perhatikan gambar !
Diketahui panjang BD = 12 cm, AE = 10 cm, dan CE = 16 cm. Luas bangun ABCD adalah . . . .
$A.\ 156\ cm^2$
$B.\ 146\ cm^2$
$C.\ 136\ cm^2$
$D.\ 126\ cm^2$
Diketahui panjang BD = 12 cm, AE = 10 cm, dan CE = 16 cm. Luas bangun ABCD adalah . . . .
$A.\ 156\ cm^2$
$B.\ 146\ cm^2$
$C.\ 136\ cm^2$
$D.\ 126\ cm^2$
$Perhatikan\ segitiga\ ABD\ !$
$\begin{align*}
alas &= BD\\
tinggi &= AE\\
Luas &= \dfrac{1}{2}.BD.AE\\
&= \dfrac{1}{2}.12.10\\
&= 60\ cm^2\\
\end{align*}$
$Perhatikan\ segitiga\ BCD\ !$
$\begin{align*}
alas &= BD\\
tinggi &= CE\\
Luas &= \dfrac{1}{2}.BD.CE\\
&= \dfrac{1}{2}.12.16\\
&= 96\ cm^2\\
Luas\ ABCD &= luas\ \Delta ABD + luas\ \Delta BCD\\
&= 60 + 96\\
&= 156\ cm^2 → A.
\end{align*}$
$\begin{align*}
alas &= BD\\
tinggi &= AE\\
Luas &= \dfrac{1}{2}.BD.AE\\
&= \dfrac{1}{2}.12.10\\
&= 60\ cm^2\\
\end{align*}$
$Perhatikan\ segitiga\ BCD\ !$
$\begin{align*}
alas &= BD\\
tinggi &= CE\\
Luas &= \dfrac{1}{2}.BD.CE\\
&= \dfrac{1}{2}.12.16\\
&= 96\ cm^2\\
Luas\ ABCD &= luas\ \Delta ABD + luas\ \Delta BCD\\
&= 60 + 96\\
&= 156\ cm^2 → A.
\end{align*}$
20. Perhatikan gambar !
Diketahui panjang AB = 16 cm, DF = 12 cm, CH = 12 cm, dan EG = 5 cm. Luas bangun ADEBCE adalah . . . .
$A.\ 96\ cm^2$
$B.\ 108\ cm^2$
$C.\ 116\ cm^2$
$D.\ 148\ cm^2$
Diketahui panjang AB = 16 cm, DF = 12 cm, CH = 12 cm, dan EG = 5 cm. Luas bangun ADEBCE adalah . . . .
$A.\ 96\ cm^2$
$B.\ 108\ cm^2$
$C.\ 116\ cm^2$
$D.\ 148\ cm^2$
$\begin{align*}
Luas\ \Delta ABD &= \dfrac{1}{2}.AB.DF\\
&= \dfrac{1}{2}.16.12\\
&= 96\ cm^2\\
Luas\ \Delta ABC &= \dfrac{1}{2}.AB.CH\\
&= \dfrac{1}{2}.16.10\\
&= 80\ cm^2\\
Luas\ \Delta ABE &= \dfrac{1}{2}.AB.EG\\
&= \dfrac{1}{2}.16.5\\
&= 40\ cm^2\\
Luas\ \Delta AED &= luas\ \Delta ABD - luas\ \Delta ABE\\
Luas\ \Delta AED &= 96 - 40\\
Luas\ \Delta AED &= 56\ cm^2\\
Luas\ \Delta BCE &= luas\ \Delta ABC - luas\ \Delta ABE\\
Luas\ \Delta BCE &= 80 - 40\\
Luas\ \Delta BCE &= 40\ cm^2\\
Luas\ ADEBCE &= luas\ \Delta AED + luas\ \Delta BCE\\
Luas\ ADEBCE &= 56 + 40\\
Luas\ ADEBCE &= 96\ cm^2. → A.
\end{align*}$
Luas\ \Delta ABD &= \dfrac{1}{2}.AB.DF\\
&= \dfrac{1}{2}.16.12\\
&= 96\ cm^2\\
Luas\ \Delta ABC &= \dfrac{1}{2}.AB.CH\\
&= \dfrac{1}{2}.16.10\\
&= 80\ cm^2\\
Luas\ \Delta ABE &= \dfrac{1}{2}.AB.EG\\
&= \dfrac{1}{2}.16.5\\
&= 40\ cm^2\\
Luas\ \Delta AED &= luas\ \Delta ABD - luas\ \Delta ABE\\
Luas\ \Delta AED &= 96 - 40\\
Luas\ \Delta AED &= 56\ cm^2\\
Luas\ \Delta BCE &= luas\ \Delta ABC - luas\ \Delta ABE\\
Luas\ \Delta BCE &= 80 - 40\\
Luas\ \Delta BCE &= 40\ cm^2\\
Luas\ ADEBCE &= luas\ \Delta AED + luas\ \Delta BCE\\
Luas\ ADEBCE &= 56 + 40\\
Luas\ ADEBCE &= 96\ cm^2. → A.
\end{align*}$
Demikianlah soal dan pembahasan bangun datar segitiga. Selamat belajar !
wwww.maretong.com



















WTF?
ReplyDelete