Soal dan Pembahasan Bangun Datar Segiempat yang dimaksud disini adalah soal dan pembahasan tentang Pengertan, sifat-sifat, rumus dan cara menghitung luas dan keliling persegi panjang, persegi, jajargenjang, belah ketupat, layang-layang, dan trapesium.
Perhatikan gambar!
Persegi memiliki sifat-sifat sebagai berikut:
$\bullet$ Memiliki dua pasang sisi sejajar dan empat sisi sama panjang. AB = BC = CD = AD.
$\bullet$ Memiliki dua buah diagonal yang sama panjang dan berpotongan saling membagi dua sama panjang. AO = BO = CO = DO.
$\bullet$ Diagonal-diagonal saling berpotongan dengan membentuk sudut siku-siku. $\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^o$.
$\bullet$ Memiliki empat titik sudut dan setiap sudut persegi adalah sama besar dan merupakan sudut siku-siku. $\angle BAD = \angle ABC = \angle BCD = \angle ADC = 90^o$.
$\bullet$ Diagonal-diagonal persegi merupakan garis bagi, yang membagi sudut-sudut persegi menjadi dua bagian yang sama besar.
$\angle BAC = \angle DAC = 45^o$
$\angle ABD = \angle CBD = 45^o$
$\angle ACB = \angle ACD = 45^o$
$\angle ADB = \angle BDC = 45^o$
$\bullet$ Memiliki 4 buah sumbu simetri.
$\bullet$ Dapat menempati bingkainya dengan 8 cara.
$L = s^2\ atau\ L = s \times s.$
L = luas
s = panjang sisi
Rumus Keliling Persegi
$K = 4 \times s\ atau\ K = 4s$
K = keliling
s = panjang sisi
Perhatikan gambar !
Persegi panjang memiliki sifat-sifat sebagai berikut:
$\bullet$ Mempunyai empat sisi dengan dua pasang sisi yang sejajar, dimana sisi-sisi yang sejajar sama panjang.
AB // DC dan AB = DC.
AD // BC dan AD = BC.
$\bullet$ Memiliki dua buah diagonal yang sama panjang. AC = BD.
$\bullet$ Kedua buah diadonal saling berpotongan sama panjang. AO = BO = CO = DO.
$\bullet$ Memiliki 4 titik sudut dan setiap sudut sama besar dan merupakan sudut siku-siku.
$\bullet$ Memiliki dua buah sumbu simetri.
$\bullet$ Dapat menempati bingkainya dengan 4 cara.
$L = p \times l\ atau\ L = pl$
L = luas
p = panjang
l = lebar
Rumus Keliling Persegi Panjang
$K = 2p + 2l$
$K = 2(p + l)$
K = keliling
p = panjang
l = lebar
Perhatikan gambar !
Jajargenjang mempunyai sifat-sifat sebagai berikut:
$\bullet$ Sisi-sisi yang berhadapan, sejajar dan sama panjang.
AB // CD dan AB = CD.
AD // BC dan AD = BC
$\bullet$ Sudut-sudut yang berhadapan sama besar.
$\angle BAD = \angle BCD$
$\angle ABC = \angle ADC$
$\bullet$ Jumlah dua buah sudut yang berdekatan adalah $180^o$
$\angle BAD + \angle ADC = 180^o$
$\angle BAD + \angle ABC = 180^o$
$\angle ABC + \angle BCD = 180^o$
$\angle ADC + \angle BCD = 180^o$
$\bullet$ Kedua diagonal saling berpotongan dan saling membagi dua sama panjang.
AO = CO
BO = DO
Luas jajargenjang = alas x tinggi.
$L = AB.DE$
AB = alas
DE = tinggi
$L = BC.DF$
BC = alas
DF = tinggi
Rumus Keliling Jajargenjang
K = AB + BC + CD + DA
K = keliling
Perhatikan gambar !
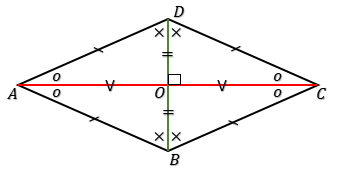
Belah ketupat mempunyai sifat-sifat sebagai berikut:
$\bullet$ Memiliki 4 buah sisi yang sama panjang.
AB = BC = CD = AD
$\bullet$ Dua buah diagonal saling berpotongan tegak lurus dan saling membagi dua sama panjang.
AO = CO
BO = DO
$\bullet$ Diagonal-diagonalnya merupakan sumbu simetri dan masing-masing membagi dua sudut sama besar.
$\angle BAC = \angle DAC = \angle BCA = \angle DCA$
$\angle ABD = \angle CBD = \angle ADB = \angle CDB$
$\bullet$ Sudut-sudut yang berhadapan sama besar.
$\angle ABC = \angle ADC$
$\angle BAD = \angle BCD$
$\bullet$ Dua buah sudut yang berdekatan jumlahnya $180^o$.
$\angle A + \angle B = 180^o$
$\angle B + \angle C = 180^o$
$\angle C + \angle D = 180^o$
$\angle A + \angle D = 180^o$
$L = \dfrac{1}{2}d_1.d_2$
$d_1 = AC$ → diagonal 1.
$d_2 = BD$ → diagonal 2.
Rumus Keliling Belah Ketupat
K = AB + BC + CD + AD
K = 4s
K = keliling
s = panjang sisi
Perhatikan gambar !
Layang-layang mempunyai sifat-sifat sebagai berikut:
$\bullet$ Memiliki sepasang-sepasang sisi yang sama panjang.
AB = AD
BC = CD
$\bullet$ Salah satu diagonal memotong diagonal lainnya sama panjang. AC memotong BD dan membagi BD menjadi dua
sama panjang.
BO = DO.
$\bullet$ Kedua diagonal berpotongan saling tegak lurus.
$\bullet$ Salah satu diagonalnya merupakan sumbu simetri. AC merupakan sumbu simetri.
$\bullet$ Memiliki sepasang sudut yang berhadapan sama besar. $\angle ABC = \angle ADC$
$L = \dfrac{1}{2}d_1.d_2$
$d_1 = AC$ → diagonal 1.
$d_2 = BD$ → diagonal 2.
Rumus Keliling Layang-layang
K = AB + BC + CD + AD
K = 2(AB + BC)
L = luas
K = keliling
$\bullet$ Jika sepasang sisi yang bukan sisi sejajar sama panjang, maka trapesium tersebut disebut trapesium sama kaki.
$\bullet$ Jika sisi-sisi yang sejajar tegak lurus terhadap salah satu sisi yang bukan sisi sejajar, maka trapesium disebut trapesium siku-siku.
$\bullet$ Jika empat sisi masing-masing memiliki panjang yang berbeda, maka trapesium disebut trapesium sembarang.
Perhatikan gambar !
Sifat trapesium adalah:
$\bullet$ Jumlah dua buah sudut yang berdekatan diantara dua garis sejajar adalah $180^o$.
$\angle A + \angle D = 180^o$
$\angle B + \angle C = 180^o$
$L = \dfrac{1}{2}(a + b).t$
Rumus Keliling Trapesium
K = AB + BC + CD + AD
Sudut yang berhadapan sama besar, sehingga:
$\angle A = \angle C$
$(x + 10)^o = (3x - 20)^o$
$x + 10 = 3x - 20$
$10 + 20 = 3x - x$
$30 = 2x$
$15 = x$
$\angle A = (x + 10)^o$
$= (15 + 10)^o$
$= 25^o$
$\angle A + \angle D = 180^o$
$25^o + \angle D = 180^o$
$\angle D = 180^o - 25^o$
$\angle D = 155^o$ → C.
$\angle ABD = \angle ADB = 70^o$
$\angle ABD + \angle ADB + \angle BAD = 180^o$
$70^o + 70^o + \angle BAD = 180^o$
$140^o + \angle BAD = 180^o$
$\angle BAD = 180^o - 140^o$
$\angle BAD = 40^o$
$\angle BAC = \dfrac{1}{2}\angle BAD$
$\angle BAC = \dfrac{1}{2}.40^o$
$\angle BAC = 20^o$ → A.
Demikianlah soal dan pembahasan bangun datar segi empat. Selamat belajar !
SHARE THIS POST
www.maretong.com
Daftar isi
PERSEGI
Pengertian dan Sifat-sifat Persegi
Persegi adalah bidang datar segiempat atau bidang dua dimensi yang memiliki luas, tetapi tidak memiliki volume.Perhatikan gambar!
Persegi memiliki sifat-sifat sebagai berikut:
$\bullet$ Memiliki dua pasang sisi sejajar dan empat sisi sama panjang. AB = BC = CD = AD.
$\bullet$ Memiliki dua buah diagonal yang sama panjang dan berpotongan saling membagi dua sama panjang. AO = BO = CO = DO.
$\bullet$ Diagonal-diagonal saling berpotongan dengan membentuk sudut siku-siku. $\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^o$.
$\bullet$ Memiliki empat titik sudut dan setiap sudut persegi adalah sama besar dan merupakan sudut siku-siku. $\angle BAD = \angle ABC = \angle BCD = \angle ADC = 90^o$.
$\bullet$ Diagonal-diagonal persegi merupakan garis bagi, yang membagi sudut-sudut persegi menjadi dua bagian yang sama besar.
$\angle BAC = \angle DAC = 45^o$
$\angle ABD = \angle CBD = 45^o$
$\angle ACB = \angle ACD = 45^o$
$\angle ADB = \angle BDC = 45^o$
$\bullet$ Memiliki 4 buah sumbu simetri.
$\bullet$ Dapat menempati bingkainya dengan 8 cara.
Rumus Luas dan Rumus Keliling Persegi
Rumus Luas Persegi$L = s^2\ atau\ L = s \times s.$
L = luas
s = panjang sisi
Rumus Keliling Persegi
$K = 4 \times s\ atau\ K = 4s$
K = keliling
s = panjang sisi
PERSEGI PANJANG
Pengertian dan Sifat-sifat Persegipanjang
Persegi panjang adalah bangun datar atau bangun dua dimensi yang memiliki luas dan tidak memiliki volume.Perhatikan gambar !
Persegi panjang memiliki sifat-sifat sebagai berikut:
$\bullet$ Mempunyai empat sisi dengan dua pasang sisi yang sejajar, dimana sisi-sisi yang sejajar sama panjang.
AB // DC dan AB = DC.
AD // BC dan AD = BC.
$\bullet$ Memiliki dua buah diagonal yang sama panjang. AC = BD.
$\bullet$ Kedua buah diadonal saling berpotongan sama panjang. AO = BO = CO = DO.
$\bullet$ Memiliki 4 titik sudut dan setiap sudut sama besar dan merupakan sudut siku-siku.
$\bullet$ Memiliki dua buah sumbu simetri.
$\bullet$ Dapat menempati bingkainya dengan 4 cara.
Rumus Luas dan Rumus Keliling Persegipanjang
Rumus Luas Persegi Panjang$L = p \times l\ atau\ L = pl$
L = luas
p = panjang
l = lebar
Rumus Keliling Persegi Panjang
$K = 2p + 2l$
$K = 2(p + l)$
K = keliling
p = panjang
l = lebar
JAJARGENJANG
Pengertian dan Sifat-sifat Jajargenjang
Jajargenjang adalah bangun datar atau bangun dua dimensi yang memiliki luas dan tidak memiliki volume. Jajargenjang dibentuk oleh dua buah segitiga sebangun.Perhatikan gambar !
Jajargenjang mempunyai sifat-sifat sebagai berikut:
$\bullet$ Sisi-sisi yang berhadapan, sejajar dan sama panjang.
AB // CD dan AB = CD.
AD // BC dan AD = BC
$\bullet$ Sudut-sudut yang berhadapan sama besar.
$\angle BAD = \angle BCD$
$\angle ABC = \angle ADC$
$\bullet$ Jumlah dua buah sudut yang berdekatan adalah $180^o$
$\angle BAD + \angle ADC = 180^o$
$\angle BAD + \angle ABC = 180^o$
$\angle ABC + \angle BCD = 180^o$
$\angle ADC + \angle BCD = 180^o$
$\bullet$ Kedua diagonal saling berpotongan dan saling membagi dua sama panjang.
AO = CO
BO = DO
Rumus luas dan Rumus Keliling Jajargenjang
Rumus Luas jajargenjangLuas jajargenjang = alas x tinggi.
$L = AB.DE$
AB = alas
DE = tinggi
$L = BC.DF$
BC = alas
DF = tinggi
Rumus Keliling Jajargenjang
K = AB + BC + CD + DA
K = keliling
BELAH KETUPAT
Pengertian dan Sifat-sifat Belah Ketupat
Belah ketupat adalah bangun datar yang merupakan gabungan dua buah segitiga sama kaki. Jika sebuah segitiga sama kaki dicerminkan terhadap alasnya, maka akan terbentuk sebuah belah ketupat.Perhatikan gambar !
Belah ketupat mempunyai sifat-sifat sebagai berikut:
$\bullet$ Memiliki 4 buah sisi yang sama panjang.
AB = BC = CD = AD
$\bullet$ Dua buah diagonal saling berpotongan tegak lurus dan saling membagi dua sama panjang.
AO = CO
BO = DO
$\bullet$ Diagonal-diagonalnya merupakan sumbu simetri dan masing-masing membagi dua sudut sama besar.
$\angle BAC = \angle DAC = \angle BCA = \angle DCA$
$\angle ABD = \angle CBD = \angle ADB = \angle CDB$
$\bullet$ Sudut-sudut yang berhadapan sama besar.
$\angle ABC = \angle ADC$
$\angle BAD = \angle BCD$
$\bullet$ Dua buah sudut yang berdekatan jumlahnya $180^o$.
$\angle A + \angle B = 180^o$
$\angle B + \angle C = 180^o$
$\angle C + \angle D = 180^o$
$\angle A + \angle D = 180^o$
Rumus Luas dan Rumus Keliling Belah Ketupat
Rumus Luas Belah Ketupat$L = \dfrac{1}{2}d_1.d_2$
$d_1 = AC$ → diagonal 1.
$d_2 = BD$ → diagonal 2.
Rumus Keliling Belah Ketupat
K = AB + BC + CD + AD
K = 4s
K = keliling
s = panjang sisi
LAYANG-LAYANG
Pengertian dan Sifat-sifat Layang-layang
Layang-layang adalah bangun datar yang terbentuk dari dua buah segitiga sama kaki yang alasnya berimpit.Perhatikan gambar !
Layang-layang mempunyai sifat-sifat sebagai berikut:
$\bullet$ Memiliki sepasang-sepasang sisi yang sama panjang.
AB = AD
BC = CD
$\bullet$ Salah satu diagonal memotong diagonal lainnya sama panjang. AC memotong BD dan membagi BD menjadi dua
sama panjang.
BO = DO.
$\bullet$ Kedua diagonal berpotongan saling tegak lurus.
$\bullet$ Salah satu diagonalnya merupakan sumbu simetri. AC merupakan sumbu simetri.
$\bullet$ Memiliki sepasang sudut yang berhadapan sama besar. $\angle ABC = \angle ADC$
Rumus Luas dan Rumus Keliling Layang-layang
Rumus Luas Layang-layang$L = \dfrac{1}{2}d_1.d_2$
$d_1 = AC$ → diagonal 1.
$d_2 = BD$ → diagonal 2.
Rumus Keliling Layang-layang
K = AB + BC + CD + AD
K = 2(AB + BC)
L = luas
K = keliling
TRAPESIUM
Pengertian dan Sifat-sifat Trapesium
Trapesium adalah bangun datar segi empat yang memiliki sepasang sisi yang berhadapan dan sejajar.$\bullet$ Jika sepasang sisi yang bukan sisi sejajar sama panjang, maka trapesium tersebut disebut trapesium sama kaki.
$\bullet$ Jika sisi-sisi yang sejajar tegak lurus terhadap salah satu sisi yang bukan sisi sejajar, maka trapesium disebut trapesium siku-siku.
$\bullet$ Jika empat sisi masing-masing memiliki panjang yang berbeda, maka trapesium disebut trapesium sembarang.
Perhatikan gambar !
Sifat trapesium adalah:
$\bullet$ Jumlah dua buah sudut yang berdekatan diantara dua garis sejajar adalah $180^o$.
$\angle A + \angle D = 180^o$
$\angle B + \angle C = 180^o$
Rumus Luas dan Rumus Keliling Trapesium
Rumus Luas Trapesium$L = \dfrac{1}{2}(a + b).t$
Rumus Keliling Trapesium
K = AB + BC + CD + AD
Contoh Soal dan Pembahasan Bangun Datar Segi Empat
1. Panjang diagonal-diagonal persegi panjang adalah $(4x + 2)$ cm dan $(6x - 16)$ cm. Panjang diagonal persegi panjang tersebut adalah . . . .
A. 35 cm
B. 36 cm
C. 37 cm
D. 38 cm
A. 35 cm
B. 36 cm
C. 37 cm
D. 38 cm
Diagonal-diagonal persegi panjang pasti sama panjang, sehingga:
$4x + 2 = 6x - 16$
$2 + 16 = 6x - 4x$
$18 = 2x$
$x = 9$
$Panjang\ diagonal = 4x + 2$
$= 4.9 + 2$
$= 38\ cm$ → D.
$4x + 2 = 6x - 16$
$2 + 16 = 6x - 4x$
$18 = 2x$
$x = 9$
$Panjang\ diagonal = 4x + 2$
$= 4.9 + 2$
$= 38\ cm$ → D.
2. Keliling persegi panjang adalah 36 cm, sedangkan lebarnya 8 cm. Luas persegi panjang tersebut adalah . . . .
$A.\: 70\:cm^2$
$B.\: 80\:cm^2$
$C.\: 90\:cm^2$
$D.\: 108\:cm^2$
$A.\: 70\:cm^2$
$B.\: 80\:cm^2$
$C.\: 90\:cm^2$
$D.\: 108\:cm^2$
$K = 2p + 2l$
$36 = 2p + 2.8$
$36 = 2p + 16$
$36 - 16 = 2p$
$20 = 2p$
$p = 10\ cm$
$L = pl$
$= 10.8$
$= 80\;cm^2$ → B.
$36 = 2p + 2.8$
$36 = 2p + 16$
$36 - 16 = 2p$
$20 = 2p$
$p = 10\ cm$
$L = pl$
$= 10.8$
$= 80\;cm^2$ → B.
3. Diketahui keliling persegi adalah 68 cm. Luas persegi tersebut adalah . . . .
$A.\: 196\ cm^2$
$B.\: 225\ cm^2$
$C.\: 289\ cm^2$
$D.\: 324\ cm^2$
$A.\: 196\ cm^2$
$B.\: 225\ cm^2$
$C.\: 289\ cm^2$
$D.\: 324\ cm^2$
$K = 4s$
$68 = 4s$
$17 = s$
$L = s.s$
$= 17.17$
$= 289\; cm^2 → C.$
$68 = 4s$
$17 = s$
$L = s.s$
$= 17.17$
$= 289\; cm^2 → C.$
4. Diketahui luas persegi adalah $225\; cm^2$. Keliling persegi tersebut adalah . . . .
A. 40 cm
B. 50 cm
C. 60 cm
D. 70 cm
A. 40 cm
B. 50 cm
C. 60 cm
D. 70 cm
$L = s^2$
$225 = s^2$
$s = \sqrt{225}$
$s = 15$ cm
$K = 4s$
$= 4.15$
$= 60$ cm → C.
$225 = s^2$
$s = \sqrt{225}$
$s = 15$ cm
$K = 4s$
$= 4.15$
$= 60$ cm → C.
5. Diketahui jajargenjang ABCD, $\angle A\: : \:\angle B = 4\: : \:5$. Besar $\angle A$ adalah . . . .
$A.\: 50^o$
$B.\: 60^o$
$C.\: 70^o$
$D.\: 80^o$
$A.\: 50^o$
$B.\: 60^o$
$C.\: 70^o$
$D.\: 80^o$
Lihat gambar !
Misalkan:
$\angle A = 4n$
$\angle B = 5n$
$\angle A + \angle B = 180^o$
$4n + 5n = 180^o$
$9n = 180^o$
$n = 20^o$
$\angle A = 4n$
$= 4.20^o$
$= 80^o$ → D.
Misalkan:
$\angle A = 4n$
$\angle B = 5n$
$\angle A + \angle B = 180^o$
$4n + 5n = 180^o$
$9n = 180^o$
$n = 20^o$
$\angle A = 4n$
$= 4.20^o$
$= 80^o$ → D.
6. Diketahui jajargenjang ABCD, $\angle A = (x + 10)^o$ dan $\angle C = (3x - 20)^o$. Besar $\angle D$ adalah . . . .
$A.\: 120^o$
$B.\: 135^o$
$C.\: 155^o$
$D.\: 160^o$
$A.\: 120^o$
$B.\: 135^o$
$C.\: 155^o$
$D.\: 160^o$
Sudut yang berhadapan sama besar, sehingga:
$\angle A = \angle C$
$(x + 10)^o = (3x - 20)^o$
$x + 10 = 3x - 20$
$10 + 20 = 3x - x$
$30 = 2x$
$15 = x$
$\angle A = (x + 10)^o$
$= (15 + 10)^o$
$= 25^o$
$\angle A + \angle D = 180^o$
$25^o + \angle D = 180^o$
$\angle D = 180^o - 25^o$
$\angle D = 155^o$ → C.
7. Perhatikan gambar !
Luas jajargenjang PQRS adalah . . . .
$A.\: 60\ cm^2$
$B.\: 70\ cm^2$
$C.\: 80\ cm^2$
$D.\: 90\ cm^2$
Luas jajargenjang PQRS adalah . . . .
$A.\: 60\ cm^2$
$B.\: 70\ cm^2$
$C.\: 80\ cm^2$
$D.\: 90\ cm^2$
PS = QR = 10 cm
$L = alas\;\times\;tinggi$
$L = QR.ST$
$L = 10.8$
$L = 80 \;cm^2$ → C.
$L = alas\;\times\;tinggi$
$L = QR.ST$
$L = 10.8$
$L = 80 \;cm^2$ → C.
8. Perhatikan gambar !
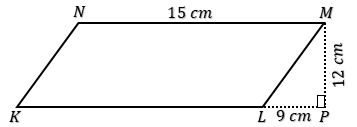
Luas jajargenjang KLMN adalah . . . .
$A.\; 150\; cm^2$
$B.\; 160\; cm^2$
$C.\; 180\; cm^2$
$D.\; 190\; cm^2$
Luas jajargenjang KLMN adalah . . . .
$A.\; 150\; cm^2$
$B.\; 160\; cm^2$
$C.\; 180\; cm^2$
$D.\; 190\; cm^2$
MN = KL = 15 cm
$L = alas\;\times\;tinggi$
$L = KL.MP$
$L = 15.12$
$L = 180 \;cm^2$ → C.
$L = alas\;\times\;tinggi$
$L = KL.MP$
$L = 15.12$
$L = 180 \;cm^2$ → C.
9. Diketahui jajargenjang ABCD, panjang AB = 12 cm, AD = 16 cm, CE = 9 cm.
Panjang CF adalah . . . .
A. 12 cm
B. 14 cm
C. 16 cm
D. 18 cm
Panjang CF adalah . . . .
A. 12 cm
B. 14 cm
C. 16 cm
D. 18 cm
Luas = AB x CF
Luas = AD x CE
sehingga:
AB x CF = AD x CE
12 x CF = 16 x 9
CF = 16 x 9 : 12
CF = 12 cm → A.
Luas = AD x CE
sehingga:
AB x CF = AD x CE
12 x CF = 16 x 9
CF = 16 x 9 : 12
CF = 12 cm → A.
10. Panjang alas dan tinggi suatu jajargenjang berbanding sebagai 3 : 2. Jika luas jajargenjang tersebut adalah 216 $cm^2$, maka tinggi jajargenjang tersebut adalah . . . .
A. 8 cm
B. 10 cm
C. 12 cm
D. 15 cm
A. 8 cm
B. 10 cm
C. 12 cm
D. 15 cm
Misalkan:
panjang alas = 3n
tinggi = 2n
Luas = alas x tinggi
$216 = 3n.2n$
$216 = 6n^2$
$36 = n^2$
$n = \sqrt{36}$
$n = 6$
Tinggi = 2n
= 2.6
= 12 cm → C.
panjang alas = 3n
tinggi = 2n
Luas = alas x tinggi
$216 = 3n.2n$
$216 = 6n^2$
$36 = n^2$
$n = \sqrt{36}$
$n = 6$
Tinggi = 2n
= 2.6
= 12 cm → C.
11. Diketahui belah ketupat ABCD. Jika besar $\angle ABD = 70^o$ maka besar $\angle BAC$ adalah . . . .
$A.\ 20^o$
$B.\ 30^o$
$C.\ 40^o$
$D.\ 50^o$
$A.\ 20^o$
$B.\ 30^o$
$C.\ 40^o$
$D.\ 50^o$
$\angle ABD = \angle ADB = 70^o$
$\angle ABD + \angle ADB + \angle BAD = 180^o$
$70^o + 70^o + \angle BAD = 180^o$
$140^o + \angle BAD = 180^o$
$\angle BAD = 180^o - 140^o$
$\angle BAD = 40^o$
$\angle BAC = \dfrac{1}{2}\angle BAD$
$\angle BAC = \dfrac{1}{2}.40^o$
$\angle BAC = 20^o$ → A.
12. Panjang diagonal-diagonal belah ketupat adalah 12 cm dan 16 cm. Luas belah ketupat tersebut adalah . . . .
$A.\ 48\ cm^2$
$B.\ 64\ cm^2$
$C.\ 96\ cm^2$
$D.\ 108\ cm^2$
$A.\ 48\ cm^2$
$B.\ 64\ cm^2$
$C.\ 96\ cm^2$
$D.\ 108\ cm^2$
$L = \dfrac{1}{2}.D_1.D_2$
$= \dfrac{1}{2}.12.16$
$= 96\ cm^2$ → C.
$= \dfrac{1}{2}.12.16$
$= 96\ cm^2$ → C.
13. Luas sebuah belah ketupat adalah $120\ cm^2$ dan panjang salah satu diagonalnya adalah $20\ cm$. Panjang diagonal yang lainnya adalah . . . .
$A.\ 10\ cm$
$B.\ 12\ cm$
$C.\ 15\ cm$
$D.\ 18\ cm$
$A.\ 10\ cm$
$B.\ 12\ cm$
$C.\ 15\ cm$
$D.\ 18\ cm$
$L = \dfrac{1}{2}.D_1.D_2$
$120 = \dfrac{1}{2}.20.D_2$
$120 = 10.D_2$
$D_2 = \dfrac{120}{10}$
$12 = D_2$ → B.
$120 = \dfrac{1}{2}.20.D_2$
$120 = 10.D_2$
$D_2 = \dfrac{120}{10}$
$12 = D_2$ → B.
14. Diketahui luas sebuah belah ketupat $216\ cm^2$. Perbandingan panjang diagonal-diagonalnya adalah 3 : 4. Panjang diagonal yang terpanjang adalah . . . .
$A.\ 18\ cm$
$B.\ 24\ cm$
$C.\ 27\ cm$
$D.\ 32\ cm$
$A.\ 18\ cm$
$B.\ 24\ cm$
$C.\ 27\ cm$
$D.\ 32\ cm$
Misalkan panjang diagonal-diagonalnya adalah 3n dan 4n.
$L = \dfrac{1}{2}.D_1.D_2$
$216 = \dfrac{1}{2}.3n.4n$
$216 = 6n^2$
$n^2 = \dfrac{216}{6}$
$36 = n^2$
$n = 6$
Panjang diagonal-diagonalnya adalah:
3n = 3.6 = 18
4n = 4.6 = 24
Panjang diagonal terpanjang = 24 cm → B.
$L = \dfrac{1}{2}.D_1.D_2$
$216 = \dfrac{1}{2}.3n.4n$
$216 = 6n^2$
$n^2 = \dfrac{216}{6}$
$36 = n^2$
$n = 6$
Panjang diagonal-diagonalnya adalah:
3n = 3.6 = 18
4n = 4.6 = 24
Panjang diagonal terpanjang = 24 cm → B.
15. Panjang diagonal-diagonal suatu layang-layang adalah 28 cm dan 42 cm. Luas layang-layang tersebut adalah . . . .
$A.\ 1176\ cm^2$
$B.\ 588\ cm^2$
$C.\ 294\ cm^2$
$D.\ 147\ cm^2$
$A.\ 1176\ cm^2$
$B.\ 588\ cm^2$
$C.\ 294\ cm^2$
$D.\ 147\ cm^2$
$L = \dfrac{1}{2}.D_1.D_2$
$L = \dfrac{1}{2}.28.42$
$L = 588\ cm^2 → B.$
$L = \dfrac{1}{2}.28.42$
$L = 588\ cm^2 → B.$
16. Keliling sebuah taman berbentuk belah ketupat adalah 104 meter dan panjang salah satu diagonalnya 20 meter. Luas taman tersebut adalah . . . .
$A.\ 320\ m^2$
$B.\ 480\ m^2$
$C.\ 640\ m^2$
$D.\ 960\ m^2$
[Soal UN]
$A.\ 320\ m^2$
$B.\ 480\ m^2$
$C.\ 640\ m^2$
$D.\ 960\ m^2$
[Soal UN]
Sisi-sisi belah ketupat adalah sama panjang. Misalkan panjang sisinya = x meter, maka:
$4x = 104$
$x = \dfrac{104}{4}$
$x = 26\ meter$
Perhatikan gambar !
Diagonal-diagonalnya adalah AC dan BD.
Dengan Dalil Phytagoras:
$OA^2 + OD^2 = AD^2$
$OD^2 = AD^2 - OA^2$
$= 26^2 - 10^2$
$= 676 - 100$
$= 576$
$OD = \sqrt{576}$
$= 24\ meter$
$BD = 2.OD$
$= 2.24$
$= 48\ meter$
$L = \dfrac{1}{2}.AC.BD$
$= \dfrac{1}{2}.20.48$
$= 480\ m^2$ → B.
$4x = 104$
$x = \dfrac{104}{4}$
$x = 26\ meter$
Perhatikan gambar !
Diagonal-diagonalnya adalah AC dan BD.
Dengan Dalil Phytagoras:
$OA^2 + OD^2 = AD^2$
$OD^2 = AD^2 - OA^2$
$= 26^2 - 10^2$
$= 676 - 100$
$= 576$
$OD = \sqrt{576}$
$= 24\ meter$
$BD = 2.OD$
$= 2.24$
$= 48\ meter$
$L = \dfrac{1}{2}.AC.BD$
$= \dfrac{1}{2}.20.48$
$= 480\ m^2$ → B.
17. Diketahui luas belah ketupat $240\ cm^2$ dan panjang salah satu diagonalnya $30\ cm$. Keliling belah ketupat tersebut adalah . . . .
$A.\ 60\ cm$
$B.\ 68\ cm$
$C.\ 80\ cm$
$D.\ 120\ cm$
[Soal UN]
$A.\ 60\ cm$
$B.\ 68\ cm$
$C.\ 80\ cm$
$D.\ 120\ cm$
[Soal UN]
$L = \dfrac{1}{2}.D_1.D_2$
$240 = \dfrac{1}{2}.30.D_2$
$240 = 15D_2$
$D_2 = \dfrac{240}{15}$
$16 = D_2$
Perhatikan gambar !
Dengan Dalil Phytagoras:
$AD^2 = OA^2 + OD^2$
$= 15^2 + 8^2$
$= 225 + 64$
$= 289$
$AD = \sqrt{289}$
$= 17\ cm$
Panjang sisi-sisi belah ketupat adalah sama.
$AB = BC = CD = AD$
$Keliling = 4.AD$
$= 4.17$
$= 68\ cm$ → B.
$240 = \dfrac{1}{2}.30.D_2$
$240 = 15D_2$
$D_2 = \dfrac{240}{15}$
$16 = D_2$
Perhatikan gambar !
Dengan Dalil Phytagoras:
$AD^2 = OA^2 + OD^2$
$= 15^2 + 8^2$
$= 225 + 64$
$= 289$
$AD = \sqrt{289}$
$= 17\ cm$
Panjang sisi-sisi belah ketupat adalah sama.
$AB = BC = CD = AD$
$Keliling = 4.AD$
$= 4.17$
$= 68\ cm$ → B.
18. Kebun berbentuk persegi panjang dengan ukuran 30 m x 20 m. Di sekeliling kebun ditanami pohon dengan jarak antar pohon 5 m. Banyak pohon yang ditanam adalah . . . .
A. 10
B. 20
C. 40
D. 120
A. 10
B. 20
C. 40
D. 120
$Keliling = 2.30 + 2.20\ cm$
$= 100\ cm$
$Banyak\ pohon = \dfrac{Keliling}{Jarak\ Pohon}$
$= \dfrac{100}{ 5}$
$= 20$ → B.
$= 100\ cm$
$Banyak\ pohon = \dfrac{Keliling}{Jarak\ Pohon}$
$= \dfrac{100}{ 5}$
$= 20$ → B.
19. Sebuah kolam renang berbentuk persegi panjang, mempunyai ukuran panjang 20 meter dan lebar 10 meter. Disekeliling kolam renang bagian luar akan dibuat jalan dengan lebar 1 meter. Jika jalan akan dipasang keramik dengan biaya Rp60.000,00 setiap meter persegi, maka biaya yang diperlukan untuk pemasangan keramik adalah . . . .
A. Rp1.860.000,00
B. Rp3.600.000,00
C. Rp3.840.000,00
D. Rp12.000.000,00
A. Rp1.860.000,00
B. Rp3.600.000,00
C. Rp3.840.000,00
D. Rp12.000.000,00
Perhatikan gambar !
Panjang kolam = AB
= 20 meter.
Lebar kolam = BC
= 10 meter.
Karena lebar jalan 1 meter, maka KL = 22 meter.
LM = 12 meter.
Luas keramik = 22 x 12 - 20 x 10
= 264 - 200
= 64 m2
Biaya = 64 x Rp60.000,00
= Rp3.840.000,00 → C.
= 20 meter.
Lebar kolam = BC
= 10 meter.
Karena lebar jalan 1 meter, maka KL = 22 meter.
LM = 12 meter.
Luas keramik = 22 x 12 - 20 x 10
= 264 - 200
= 64 m2
Biaya = 64 x Rp60.000,00
= Rp3.840.000,00 → C.
20. Perhatikan gambar !
Luas karton yang digunakan untuk membuat bangun huruf E adalah . . . .
$A.\ 1.448\ cm^2$
$B.\ 1.356\ cm^2$
$C.\ 1.224\ cm^2$
$D.\ 924\ cm^2$
[Soal UN 2018]
Luas karton yang digunakan untuk membuat bangun huruf E adalah . . . .
$A.\ 1.448\ cm^2$
$B.\ 1.356\ cm^2$
$C.\ 1.224\ cm^2$
$D.\ 924\ cm^2$
[Soal UN 2018]
Perhatikan gambar !
$Luas = 600 + 240 + 144 + 240$
$Luas = 1.224\ cm^2$ → C.
$Luas = 600 + 240 + 144 + 240$
$Luas = 1.224\ cm^2$ → C.
21. Diketahui trapesium ABCD siku-siku di A dan AD tegak lurus AB. Panjang AB = 20 cm, BC = 13 cm, dan CD = 15 cm. Luas dari trapesium tersebut adalah . . . .
$A.\ 180\ cm^2$
$B.\ 190\ cm^2$
$C.\ 200\ cm^2$
$D.\ 210\ cm^2$
$A.\ 180\ cm^2$
$B.\ 190\ cm^2$
$C.\ 200\ cm^2$
$D.\ 210\ cm^2$
Perhatikan gambar!
$AB = 20\ cm$
$CD = 15\ cm$
$BE = AB - CD$
$= 20 - 15$
$= 5\ cm$
Perhatikan segitiga BCE !
$CE^2 = BC^2 - BE^2$
$CE^2 = 13^2 - 5^2$
$= 169 - 25$
$= 144$
$CE = \sqrt{144}$
$= 12$
$Luas = \dfrac{AB + CD}{2}.CE$
$= \dfrac{20 + 15}{ 2}.12$
$= {35.6}$
$= 210\ cm^2$ → D.
$AB = 20\ cm$
$CD = 15\ cm$
$BE = AB - CD$
$= 20 - 15$
$= 5\ cm$
Perhatikan segitiga BCE !
$CE^2 = BC^2 - BE^2$
$CE^2 = 13^2 - 5^2$
$= 169 - 25$
$= 144$
$CE = \sqrt{144}$
$= 12$
$Luas = \dfrac{AB + CD}{2}.CE$
$= \dfrac{20 + 15}{ 2}.12$
$= {35.6}$
$= 210\ cm^2$ → D.
22. Diketahui trapesium sama kaki PQRS. PQ // RS, QR = PS. Jika panjang PQ = 20 cm, RS = 8 cm, dan QR = 10 cm. Luas dari trapesium tersebut adalah . . . .
$A.\ 84\ cm^2$
$B.\ 96\ cm^2$
$C.\ 112\ cm^2$
$D.\ 118\ cm^2$
$A.\ 84\ cm^2$
$B.\ 96\ cm^2$
$C.\ 112\ cm^2$
$D.\ 118\ cm^2$
Perhatikan gambar !
$TU = RS$
$= 8\ cm$
$PT = QU$
$Misalkan\ PT = QU = x$
$PQ = PT + TU + UQ$
$20 = x + 8 + x$
$20 = 2x + 8$
$20 - 8 = 2x$
$12 = 2x$
$x = 6$
$PT = 6$
$Lihat\ \Delta PTS\ !$
$ST^2 = PS^2 - PT^2$
$= 10^2 - 6^2$
$= 100 - 36$
$= 64$
$ST = \sqrt{64}$
$= 8$
$Luas = \dfrac{PQ + RS}{2}.ST$
$= \dfrac{20 + 8}{2}.8$
$= 14.8$
$= 112\ cm^2$ → C.
$TU = RS$
$= 8\ cm$
$PT = QU$
$Misalkan\ PT = QU = x$
$PQ = PT + TU + UQ$
$20 = x + 8 + x$
$20 = 2x + 8$
$20 - 8 = 2x$
$12 = 2x$
$x = 6$
$PT = 6$
$Lihat\ \Delta PTS\ !$
$ST^2 = PS^2 - PT^2$
$= 10^2 - 6^2$
$= 100 - 36$
$= 64$
$ST = \sqrt{64}$
$= 8$
$Luas = \dfrac{PQ + RS}{2}.ST$
$= \dfrac{20 + 8}{2}.8$
$= 14.8$
$= 112\ cm^2$ → C.
23. Tinggi suatu trapesium adalah $6 cm$ dan luasnya $63\ cm^2$. Jika perbandingan sisi-sisi yang sejajar adalah 3 : 4, maka panjang sisi sejajar yang terpendek adalah . . . .
$A.\ 9\ cm$
$B.\ 12\ cm$
$C.\ 15\ cm$
$D.\ 18\ cm$
$A.\ 9\ cm$
$B.\ 12\ cm$
$C.\ 15\ cm$
$D.\ 18\ cm$
Misalkan Panjang sisi-sisi sejajar adalah 3n dan 4n.
$L = \dfrac{3n + 4n}{2}.6$
$63 = 7n.3$
$63 = 21n$
$3 = n$
$Panjang\ sisi\ terpendek = 3n$
$= 3.3$
$= 9\ cm$ → A.
$L = \dfrac{3n + 4n}{2}.6$
$63 = 7n.3$
$63 = 21n$
$3 = n$
$Panjang\ sisi\ terpendek = 3n$
$= 3.3$
$= 9\ cm$ → A.
24. Diketahui trapesium sama kaki ABCD, AB // CD dengan panjang $AB = 16\ cm$ dan $CD = 10\ cm$. Jika luas trapesium adalah $52\ cm^2$, maka keliling trapesium tersebut adalah . . . .
A. 30 cm
B. 36 cm
C. 42 cm
D. 45 cm
A. 30 cm
B. 36 cm
C. 42 cm
D. 45 cm
Perhatikan gambar !
$EF = CD$
$= 10\ cm$
$AE = BF$
$Misalkan\ AE = BF = x$
$AB = AE + EF + BF$
$16 = x + 10 + x$
$16 = 2x + 10$
$16 - 10 = 2x$
$6 = 2x$
$3 = x$
$AE = 3\ cm$
$Luas = \dfrac{AB + CD}{2}.DE$
$52 = \dfrac{16 + 10}{ 2}.DE$
$52 = 13.DE$
$4 = DE$
$Perhatikan\ \Delta AED\ !$
$AD^2 = AE^2 + DE^2$
$AD^2 = 3^2 + 4^2$
$= 9 + 16$
$= 25$
$AD = \sqrt{25}$
$= 5\ cm$
$BC = AD$
$= 5\ cm$
$Keliling = AB + BC + CD + AD$
$= 16 + 5 + 10 + 5$
$= 36\ cm$ → B.
$EF = CD$
$= 10\ cm$
$AE = BF$
$Misalkan\ AE = BF = x$
$AB = AE + EF + BF$
$16 = x + 10 + x$
$16 = 2x + 10$
$16 - 10 = 2x$
$6 = 2x$
$3 = x$
$AE = 3\ cm$
$Luas = \dfrac{AB + CD}{2}.DE$
$52 = \dfrac{16 + 10}{ 2}.DE$
$52 = 13.DE$
$4 = DE$
$Perhatikan\ \Delta AED\ !$
$AD^2 = AE^2 + DE^2$
$AD^2 = 3^2 + 4^2$
$= 9 + 16$
$= 25$
$AD = \sqrt{25}$
$= 5\ cm$
$BC = AD$
$= 5\ cm$
$Keliling = AB + BC + CD + AD$
$= 16 + 5 + 10 + 5$
$= 36\ cm$ → B.
25. Keliling sebuah persegi sama dengan keliling persegi panjang. Jika luas persegi adalah $256\ cm^2$ dan lebar persegi panjang adalah $12\ cm$, maka luas dari persegi panjang tersebut adalah . . . .
$A.\ 180\ cm^2$
$B.\ 200\ cm^2$
$C.\ 240\ cm^2$
$D.\ 320\ cm^2$
$A.\ 180\ cm^2$
$B.\ 200\ cm^2$
$C.\ 240\ cm^2$
$D.\ 320\ cm^2$
$Luas\ persegi = sisi.sisi$
$256 = sisi^2$
$sisi = \sqrt{256}$
$sisi = 16$
$Keliling\ persegi = 4.sisi$
$= 4.16$
$= 64\ cm$
$Keliling\ persegi\ panjang = 64\ cm$
$Keliling\ persegi\ panjang = 2p + 2l$
$64 = 2p + 2l$
$64 = 2p + 2.12$
$64 = 2p + 24$
$64 - 24 = 2p$
$40 = 2p$
$p = 20\ cm$
$Luas\ persegi\ panjang = p.l$
$= 20.12$
$= 240\ cm^2$ → C.
$256 = sisi^2$
$sisi = \sqrt{256}$
$sisi = 16$
$Keliling\ persegi = 4.sisi$
$= 4.16$
$= 64\ cm$
$Keliling\ persegi\ panjang = 64\ cm$
$Keliling\ persegi\ panjang = 2p + 2l$
$64 = 2p + 2l$
$64 = 2p + 2.12$
$64 = 2p + 24$
$64 - 24 = 2p$
$40 = 2p$
$p = 20\ cm$
$Luas\ persegi\ panjang = p.l$
$= 20.12$
$= 240\ cm^2$ → C.
Demikianlah soal dan pembahasan bangun datar segi empat. Selamat belajar !
www.maretong.com
Post a Comment for "Soal dan Pembahasan Bangun Datar Segiempat"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.