Daftar isi
Materi garis dan sudut matematika SMP kelas 10 serta contoh soal dan pembahasan super lengkap.
Pengertian Garis.
Garis adalah kumpulan titik-titik yang banyaknya tak terhingga dan memanjang ke dua arah berlawanan. Garis biasanya dilambangkan dengan huruf-huruf kecil seperti k, l, m, n dan lain-lain.Kedudukan Dua Garis.
1. SejajarDua garis disebut sejajar jika kedua garis tidak berpotongan atau bertemu, dan jarak kedua garis tetap. Kedua garis memiliki kemiringan atau gradien yang sama dan kedua garis terletak pada satu bidang.
Garis k sejajar dengan garis l dan garis m sejajar dengan garis n.
2. Berpotongan
Dua garis disebut berpotongan jika kedua garis bertemu di satu titik dan kedua garis terletak pada satu bidang.
Garis p berpotongan dengan garis q di titik A dan garis a berpotongan dengan garis b di titik B.
3. Berimpit
Dua garis disebut berimpit jika kedua garis berpotongan di dua titik atau lebih. Kedua garis memiliki kemiringan yang sama, dan terletak pada satu bidang.
Garis c berimpit dengan garis d dan garis e berimpit dengan garis f.
4. Bersilangan
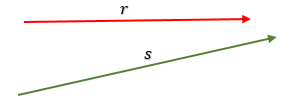
Dua garis disebut bersilangan jika kedua garis tidak sejajar dan tidak berpotongan dan kedua garis terletak pada bidang yang berbeda.
Garis r dan garis s terletak pada bidang yang berbeda, tidak berpotongan, dan tidak sejajar.
Pengertian Sudut.
Sudut adalah daerah yang dibatasi oleh dua buah sinar garis yang bertemu pada satu titik.A disebut titik pangkal atau titik sudut. Garis AB dan AC disebut kaki sudut. Daerah yang diarsir disebut besar sudut. Nama sudut adalah nama titik sudutnya, yang ditulis dengan huruf Besar (kapital), atau nama titik sudutnya diletakkan diantara huruf lain. Nama sudut di atas adalah sudut A $(\angle A)$, atau sudut BAC $(\angle BAC)$, atau sudut CAB $(\angle CAB)$. Besar sudut satu putaran penuh = $360^o$, besar sudut lurus = $180^o$, dan besar sudut siku-siku = $90^o$.
Jenis-jenis Sudut.
1. Sudut LancipSudut lancip adalah sudut yang besarnya antara $0^o$ sampai $90^o$.
2. Sudut Siku-siku
Sudut siku-siku adalah sudut yang besarnya $90^o$.
3. Sudut Tumpul
Sudut tumpul adalah sudut yang besarnya antara $90^o$ sampai $180^o$.
4. Sudut Lurus
Sudut lurus adalah sudut yang besarnya $180^o$.
Hubungan Antar Sudut
Pengertian Sudut Berpelurus (suplemen).
Dua sudut disebut berpelurus (suplemen) jika jumlah kedua sudut tersebut adalah $180^o$.$\angle ABD$ merupakan pelurus dari $\angle CBD$, atau $\angle CBD$ merupakan pelurus dari $\angle ABD$.
$\angle ABD$ + $\angle CBD$ = $180^o$
$x^o + y^o = 180^o$
Pengertian Sudut Berpenyiku (komplemen)
Dua sudut disebut berpenyiku (komplemen) jika jumlah kedua sudut tersebut adalah $90^o$.$\angle BAC$ merupakan penyiku dari $\angle CAD$, atau $\angle CAD$ merupakan penyiku dari $\angle BAC$.
$\angle BAC$ + $\angle CAD$ = $180^o$
$x^o + y^o = 180^o$.
Pengertian Sudut Bertolak Belakang.
Dua sudut bertolak belakang sama besar.$\angle AEC$ bertolak belakang dengan $\angle BED$, sehingga $\angle AEC$ = $\angle BED$
$\angle BEC$ bertolak belakang dengan $\angle AED$, sehingga $\angle BEC$ = $\angle AED$
Dua Garis Sejajar Dipotong Oleh Garis Lurus
Garis a sejajar garis b dan dipotong oleh garis k.I. Sudut-sudut yang sehadap sama besar.
$\angle A1 = \angle B1$
$\angle A2 = \angle B2$
$\angle A3 = \angle B3$
$\angle A4 = \angle B4$
II. Sudut-sudut dalam berseberangan sama besar.
$\angle A3 = \angle B1$
$\angle A4 = \angle B2$
III. Sudut-sudut luar berseberangan sama besar.
$\angle A1 = \angle B3$
$\angle A2 = \angle B4$
IV. Sudut-sudut dalam sepihak jumlahnya $180^o$.
$\angle A3 + \angle B2 = 180^o$
$\angle A4 + \angle B1 = 180^o$
V. Sudut-sudut luar sepihak jumlahnya $180^o$
$\angle A1 + \angle B4 = 180^o$
$\angle A2 + \angle B3 = 180^o$
Soal dan Pembahasan Garis dan Sudut
1. Perhatikan gambar berikut !
Pasangan sudut luar sepihak adalah . . . .
$A.\ \angle 2$ dengan $\angle 5$
$B.\ \angle 4$ dengan $\angle 8$
$C.\ \angle 2$ dengan $\angle 7$
$D.\ \angle 4$ dengan $\angle 5$
[Soal UN 2018]
Pasangan sudut luar sepihak adalah . . . .
$A.\ \angle 2$ dengan $\angle 5$
$B.\ \angle 4$ dengan $\angle 8$
$C.\ \angle 2$ dengan $\angle 7$
$D.\ \angle 4$ dengan $\angle 5$
[Soal UN 2018]
Pasangan sudut luar sepihak adalah $\angle 2$ dengan $\angle 7$ dan $\angle 1$ dengan $\angle 8$ → C.
2. Perhatikan gambar !
Pasangan sudut yang tidak sama besar adalah . . . .
$A.\ \angle A_1\ dan\ \angle B_3$
$B.\ \angle A_4\ dan\ \angle B_2$
$C.\ \angle A_2\ dan\ \angle B_2$
$D.\ \angle A_3\ dan\ \angle B_4$
[Soal UN]
Pasangan sudut yang tidak sama besar adalah . . . .
$A.\ \angle A_1\ dan\ \angle B_3$
$B.\ \angle A_4\ dan\ \angle B_2$
$C.\ \angle A_2\ dan\ \angle B_2$
$D.\ \angle A_3\ dan\ \angle B_4$
[Soal UN]
$\angle A_1\ dan\ \angle B_3$ → sudut luar berseberangan sama besar.
$\angle A_4\ dan\ \angle B_2$ → sudut luar berseberangan sama besar.
$\angle A_2\ dan\ \angle B_2$ → sudut sehadap sama besar.
$\angle A_3\ dan\ \angle B_4$ → sudut dalam sepihak jumlahnya $180^o$.
Jawab: D.
$\angle A_4\ dan\ \angle B_2$ → sudut luar berseberangan sama besar.
$\angle A_2\ dan\ \angle B_2$ → sudut sehadap sama besar.
$\angle A_3\ dan\ \angle B_4$ → sudut dalam sepihak jumlahnya $180^o$.
Jawab: D.
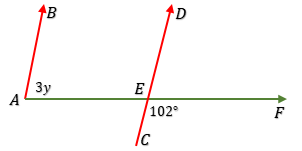
3. Perhatikan gambar dibawah ini !
Nilai y adalah . . . .
$A.\ 24^o$
$B.\ 25^o$
$C.\ 26^o$
$D.\ 34^o$
[Soal UN]
Nilai y adalah . . . .
$A.\ 24^o$
$B.\ 25^o$
$C.\ 26^o$
$D.\ 34^o$
[Soal UN]
$\angle CEF + \angle DEF = 180^o$ → sudut berpelurus.
$102^o + \angle DEF = 180^o$
$\angle DEF = 180^o - 102^o$
$\angle DEF = 78^o$
$\angle BAE = \angle DEF$
$3y = 78^o$
$y = \dfrac{78}{3}$
$y = 26^o$ → C.
$102^o + \angle DEF = 180^o$
$\angle DEF = 180^o - 102^o$
$\angle DEF = 78^o$
$\angle BAE = \angle DEF$
$3y = 78^o$
$y = \dfrac{78}{3}$
$y = 26^o$ → C.
4. Besar $\angle ABD$ pada gambar di bawah ini adalah . . . .
$A.\; 98^o$
$B.\; 105^o$
$C.\; 112^o$
$D.\; 119^o$
[Soal UN]
$A.\; 98^o$
$B.\; 105^o$
$C.\; 112^o$
$D.\; 119^o$
[Soal UN]
$\angle ABD + \angle CBD = 180^o$ → berpelurus.
$7x^o + 5x^o = 180^o$
$12x^o = 180^o$
$x = \dfrac{180}{12}$
$x = 15$
$\angle ABD = 7x^o$
$= 7.15^o$
$= 105^o$ → B.
$7x^o + 5x^o = 180^o$
$12x^o = 180^o$
$x = \dfrac{180}{12}$
$x = 15$
$\angle ABD = 7x^o$
$= 7.15^o$
$= 105^o$ → B.
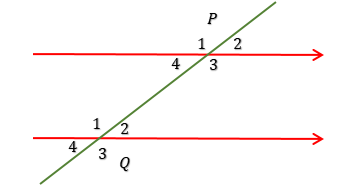
5. Perhatikan gambar di bawah ini !
Jika besar $\angle P_1 = 130^o$, besar $\angle Q_4$ adalah . . . .
$A.\ 70^o$
$B.\ 65^o$
$C.\ 50^o$
$D.\ 35^o$
[Soal UN]
Jika besar $\angle P_1 = 130^o$, besar $\angle Q_4$ adalah . . . .
$A.\ 70^o$
$B.\ 65^o$
$C.\ 50^o$
$D.\ 35^o$
[Soal UN]
$\angle P_1\ dan\ \angle Q_4$ adalah sudut luar sepihak.
$\angle P_1 + \angle Q_4 = 180^o$
$130^o + \angle Q_4 = 180^o$
$\angle Q_4 = 180^o - 130^o$
$\angle Q_4 = 50^o$ → C.
$\angle P_1 + \angle Q_4 = 180^o$
$130^o + \angle Q_4 = 180^o$
$\angle Q_4 = 180^o - 130^o$
$\angle Q_4 = 50^o$ → C.
6. Perhatikan gambar berikut !
Nilai $q$ adalah . . . .
$A.\; 68^o$
$B.\; 55^o$
$C.\; 48^o$
$D.\; 35^o$
[Soal UN]
Nilai $q$ adalah . . . .
$A.\; 68^o$
$B.\; 55^o$
$C.\; 48^o$
$D.\; 35^o$
[Soal UN]
$p = 112^o$ → sudut bertolak belakang sama besar.
$p + q = 180^o$ → sudut dalam sepihak.
$112^o + q = 180^o$
$q = 180^o - 112^o$
$q = 68^o$ → A.
$p + q = 180^o$ → sudut dalam sepihak.
$112^o + q = 180^o$
$q = 180^o - 112^o$
$q = 68^o$ → A.
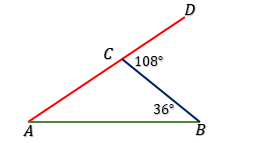
7. Perhatikan gambar !
Besar $\angle BAC$ adalah . . . .
$A.\; 24^o$
$B.\; 48^o$
$C.\; 72^o$
$D.\; 98^o$
Besar $\angle BAC$ adalah . . . .
$A.\; 24^o$
$B.\; 48^o$
$C.\; 72^o$
$D.\; 98^o$
$\angle ACB + \angle BCD = 180^o$ → berpelurus.
$\angle ACB + 108^o = 180^o$
$\angle ACB = 180^o - 108^o$
$\angle ACB = 72^o$
$\angle BAC + \angle ABC + \angle ACB = 180^o$ → jumlah sudut dalam segitiga = $180^o$
$\angle BAC + 36^o + 72^o = 180^o$
$\angle BAC + 108^o = 180^o$
$\angle BAC = 180^o - 108^o$
$\angle BAC = 72^o$ → C.
$\angle ACB + 108^o = 180^o$
$\angle ACB = 180^o - 108^o$
$\angle ACB = 72^o$
$\angle BAC + \angle ABC + \angle ACB = 180^o$ → jumlah sudut dalam segitiga = $180^o$
$\angle BAC + 36^o + 72^o = 180^o$
$\angle BAC + 108^o = 180^o$
$\angle BAC = 180^o - 108^o$
$\angle BAC = 72^o$ → C.
8. Perhatikan gambar berikut !
Besar sudut nomor 1 adalah $95^o$ dan besar sudut nomor 2 adalah $110^o$. Besar sudut nomor 3 adalah . . . .
$A.\; 5^o$
$B.\; 15^o$
$C.\; 25^o$
$D.\; 35^o$
[Soal UN]
Besar sudut nomor 1 adalah $95^o$ dan besar sudut nomor 2 adalah $110^o$. Besar sudut nomor 3 adalah . . . .
$A.\; 5^o$
$B.\; 15^o$
$C.\; 25^o$
$D.\; 35^o$
[Soal UN]
$\angle 4 = \angle 1$ → bertolak belakang.
$\angle 4 = 95^o$
$\angle 5 = \angle 4$ → sudut sehadap.
$\angle 5 = 95^o$
$\angle 2 + \angle 6 = 180^o$ → berpelurus.
$110^o + \angle 6 = 180^o$
$\angle 6 = 180^o - 110^o$
$\angle 6 = 70^o$
$\angle 3 + \angle 5 + \angle 6 = 180^o$ → sudut dalam segitiga = $180^o$.
$\angle 3 + 95^o + 70^o = 180^o$
$\angle 3 + 165^o = 180^o$
$\angle 3 = 180^o - 165^o$
$\angle 3 = 15^o$ → B.
$\angle 4 = 95^o$
$\angle 5 = \angle 4$ → sudut sehadap.
$\angle 5 = 95^o$
$\angle 2 + \angle 6 = 180^o$ → berpelurus.
$110^o + \angle 6 = 180^o$
$\angle 6 = 180^o - 110^o$
$\angle 6 = 70^o$
$\angle 3 + \angle 5 + \angle 6 = 180^o$ → sudut dalam segitiga = $180^o$.
$\angle 3 + 95^o + 70^o = 180^o$
$\angle 3 + 165^o = 180^o$
$\angle 3 = 180^o - 165^o$
$\angle 3 = 15^o$ → B.
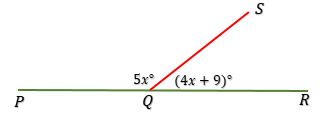
9. Perhatikan gambar berikut !
Besar pelurus sudut SQR adalah . . . .
$A.\; 101^o$
$B.\; 100^o$
$C.\; 95^o$
$D.\; 92^o$
Besar pelurus sudut SQR adalah . . . .
$A.\; 101^o$
$B.\; 100^o$
$C.\; 95^o$
$D.\; 92^o$
$\angle PQS + \angle RQS = 180^o$ → berpelurus.
$5x^o + (4x + 9)^o = 180^o$
$9x + 9 = 180$
$9x = 180 - 9$
$9x = 171$
$x = 19$
Pelurus sudut SQR adalah sudut PQS.
$\angle PQS = 5x^o$
$\angle PQS = 5.19^o$
$\angle PQS = 95^o$ → C.
$5x^o + (4x + 9)^o = 180^o$
$9x + 9 = 180$
$9x = 180 - 9$
$9x = 171$
$x = 19$
Pelurus sudut SQR adalah sudut PQS.
$\angle PQS = 5x^o$
$\angle PQS = 5.19^o$
$\angle PQS = 95^o$ → C.
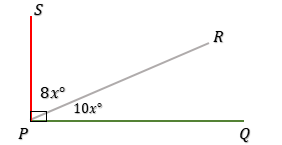
10. Perhatikan gambar dibawah !
Besar penyiku $\angle QPR$ adalah . . . .
$A.\ 15^o$
$B.\ 25^o$
$C.\ 40^o$
$D.\ 55^o$
Besar penyiku $\angle QPR$ adalah . . . .
$A.\ 15^o$
$B.\ 25^o$
$C.\ 40^o$
$D.\ 55^o$
$\angle QPR + \angle RPS = 90^o$ → berpenyiku.
$10x^o + 8x^o = 90^o$
$18x = 90$
$x = 5$
Penyiku sudut QPR adalah sudut RPS.
$\angle RPS = 8x^o$
$\angle RPS = 8.5^o$
$\angle RPS = 40^o$ → C.
$10x^o + 8x^o = 90^o$
$18x = 90$
$x = 5$
Penyiku sudut QPR adalah sudut RPS.
$\angle RPS = 8x^o$
$\angle RPS = 8.5^o$
$\angle RPS = 40^o$ → C.
11. Perhatikan gambar !
Besar pelurus $\angle CBE$ adalah . . . .
$A.\; 30^o$
$B.\; 40^o$
$C.\; 50^o$
$D.\; 60^o$
Besar pelurus $\angle CBE$ adalah . . . .
$A.\; 30^o$
$B.\; 40^o$
$C.\; 50^o$
$D.\; 60^o$
$\angle ABE + \angle DBE + \angle CBD = 180^o$ → berpelurus.
$6x^o + 8x^o + 4x^o = 180^o$
$18x = 180$
$x = 10$
Pelurus sudut CBE adalah sudut ABE.
$\angle ABE = 6x^o$
$\angle ABE = 6.10^o$
$\angle ABE = 60^o$ → D.
$6x^o + 8x^o + 4x^o = 180^o$
$18x = 180$
$x = 10$
Pelurus sudut CBE adalah sudut ABE.
$\angle ABE = 6x^o$
$\angle ABE = 6.10^o$
$\angle ABE = 60^o$ → D.
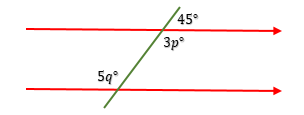
$45^o + 3p^o = 180^o$ → berpelurus.
$3p^o = 180^o - 45^o$
$3p^o = 135^o$
$p = 45$
$5q^o = 3p^o$ → dalam berseberangan.
$5q^o = 135^o$
$q = 27$
$p + q = 45 + 27$
$p + q = 72$ → A.
$3p^o = 180^o - 45^o$
$3p^o = 135^o$
$p = 45$
$5q^o = 3p^o$ → dalam berseberangan.
$5q^o = 135^o$
$q = 27$
$p + q = 45 + 27$
$p + q = 72$ → A.
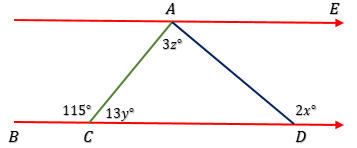
13. Perhatikan gambar berikut !
jika $\angle DAE = 46^o$, maka nilai $x + y + z = \cdots$
$A.\; 75^o$
$B.\; 85^o$
$C.\; 95^o$
$D.\; 105^o$
jika $\angle DAE = 46^o$, maka nilai $x + y + z = \cdots$
$A.\; 75^o$
$B.\; 85^o$
$C.\; 95^o$
$D.\; 105^o$
$\angle ADC = \angle DAE$ → dalam berseberangan.
$\angle ADC = 46^o$
$\angle ACB + \angle ACD = 180^o$ → berpelurus.
$115^o + 13y^o = 180^o$
$13y^o = 180^o - 115^o$
$13y^o = 65^o$
$y = 5$
$\angle ACD = 13y^o$
$\angle ACD = 65^o$
$\angle CAD + \angle ACD + \angle ADC = 180^o$
$\angle CAD + 65^o + 46^o = 180^o$
$\angle CAD + 111^o = 180^o$
$\angle CAD = 180^o - 111^o$
$\angle CAD = 69^o$
$3z^o = 69^o$
$z = 23$
$2x^o + 46^o = 180^o$ → berpelurus.
$2x^o = 180^o - 46^o$
$2x^o = 134^o$
$x = 67$
$x + y + z = 67 + 5 + 23$
$x + y + z = 95$ → C.
$\angle ADC = 46^o$
$\angle ACB + \angle ACD = 180^o$ → berpelurus.
$115^o + 13y^o = 180^o$
$13y^o = 180^o - 115^o$
$13y^o = 65^o$
$y = 5$
$\angle ACD = 13y^o$
$\angle ACD = 65^o$
$\angle CAD + \angle ACD + \angle ADC = 180^o$
$\angle CAD + 65^o + 46^o = 180^o$
$\angle CAD + 111^o = 180^o$
$\angle CAD = 180^o - 111^o$
$\angle CAD = 69^o$
$3z^o = 69^o$
$z = 23$
$2x^o + 46^o = 180^o$ → berpelurus.
$2x^o = 180^o - 46^o$
$2x^o = 134^o$
$x = 67$
$x + y + z = 67 + 5 + 23$
$x + y + z = 95$ → C.
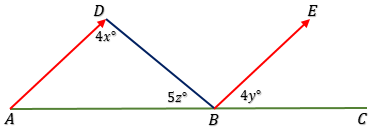
14. Perhatikan gambar !
Besar $\angle BAD = 60^o$ dan $\angle DBE = 80^o$. Nilai $x + y + z = \cdots $
$A.\ 25$
$B.\ 33$
$C.\ 35$
$D.\ 43$
Besar $\angle BAD = 60^o$ dan $\angle DBE = 80^o$. Nilai $x + y + z = \cdots $
$A.\ 25$
$B.\ 33$
$C.\ 35$
$D.\ 43$
$\angle CBE = \angle BAD$
$\angle CBE = 60^o$
$4y^o = 60^o$
$y = 15$
$\angle ABD + \angle DBE + \angle CBE = 180^o$ → berpelurus.
$5z^o + 80^o + 60^o = 180^o$
$5z^o + 140^o = 180^o$
$5z^o = 180^o - 140^o$
$5z^o = 40^o$
$z = 8$
$4x^o + 60^o + 5z^o = 180^o$ → sudut dalam segitiga.
$4x^o + 60^o + 40^o = 180^o$
$4x^o + 100^o = 180^o$
$4x^o = 80^o$
$x = 20$
$x + y + z = 20 + 15 + 8$
$x + y + z = 43$ → D.
$\angle CBE = 60^o$
$4y^o = 60^o$
$y = 15$
$\angle ABD + \angle DBE + \angle CBE = 180^o$ → berpelurus.
$5z^o + 80^o + 60^o = 180^o$
$5z^o + 140^o = 180^o$
$5z^o = 180^o - 140^o$
$5z^o = 40^o$
$z = 8$
$4x^o + 60^o + 5z^o = 180^o$ → sudut dalam segitiga.
$4x^o + 60^o + 40^o = 180^o$
$4x^o + 100^o = 180^o$
$4x^o = 80^o$
$x = 20$
$x + y + z = 20 + 15 + 8$
$x + y + z = 43$ → D.
15. Perhatikan gambar !
Diketahui $\angle CEF = 100^o$, $\angle ABC = 30^o$, $\angle BCE = (2x - 10)^o$, maka nilai $x$ yang memenuhi adalah . . . .
$A.\; 45^o$
$B.\; 50^o$
$C.\; 60^o$
$D.\; 75^o$
Diketahui $\angle CEF = 100^o$, $\angle ABC = 30^o$, $\angle BCE = (2x - 10)^o$, maka nilai $x$ yang memenuhi adalah . . . .
$A.\; 45^o$
$B.\; 50^o$
$C.\; 60^o$
$D.\; 75^o$
$\angle CED + \angle CEF = 180^o$ → berpelurus.
$\angle CED + 100^o = 180^o$
$\angle CED = 180^o - 100^o$
$\angle CED = 80^o$
Sebagian sudut BCE berseberangan dalam dengan sudut ABC dan sebagian lagi berseberangan dalam dengan sudut CED, sehingga:
$\angle ABC + \angle CED = \angle BCE$
$30^o + 80^o = 2x^o - 10^o$
$30^o + 80^o + 10^o = 2x^o$
$120^o = 2x^o$
$x = 60$ → C.
$\angle CED + 100^o = 180^o$
$\angle CED = 180^o - 100^o$
$\angle CED = 80^o$
Sebagian sudut BCE berseberangan dalam dengan sudut ABC dan sebagian lagi berseberangan dalam dengan sudut CED, sehingga:
$\angle ABC + \angle CED = \angle BCE$
$30^o + 80^o = 2x^o - 10^o$
$30^o + 80^o + 10^o = 2x^o$
$120^o = 2x^o$
$x = 60$ → C.
Demikianlah soal dan pembahasan garis dan sudut. Selamat belajar !

















Post a Comment for "Soal dan Pembahasan Garis dan Sudut"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.