Mempelajari UNBK Matematika SMA IPS 2018, sangatlah penting sebagai materi bahasan untuk persiapan menghadapi UN 2019. Karena soal dan pembahasan UN UNBK matematika SMA IPS 2018 akan menjadi sebuah sumber inspirasi yang paling baik untuk menghadapi UN UNBK yang akan datang. Sesuai dengan judulnya, maka soal yang dibahas di sini adalah soal UN UNBK matematika SMA IPS 2018. Karena sifat-sifat soal UN UNBK yang selalu mirip dari tahun ke tahun, sebaiknya adik-adik memperhatikan dengan teliti dan sungguh-sungguh setiap soal dan pembahasannya. Soal dan pembahasan UN UNBK matematika IPS 2018 ini kemungkinan besar tidaklah jauh berbeda dengan soal UN UNBK tahun 2019 yang akan datang. Pengalaman dari tahun ke tahun menunjukkan bahwa selalu ada kemiripan soal. Semoga soal dan pembahasan UN UNBK matematika SMA IPS 2018 ini bermanfaat.
Selamat Berjuang!
$1$. Bentuk sederhana dari $\left(\dfrac{5p^{-2} q^2}{25p^3 q^4} \right)^{-1}$ adalah . . . .
$A.\ 25p^5q^2$
$B.\ 5p^5q^2$
$C.\ p^5q^2$
$D.\ \dfrac{1}{5}p^5q^2$
$E.\ \dfrac{1}{25}p^5q^2$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 1.
Ingat !
$\left(\dfrac{a}{b}\right)^{-n} = \left(\dfrac{b}{a}\right)^{n}$
$\left(\dfrac{5p^{-2} q^2}{25p^3 q^4} \right)^{-1} = \left(\dfrac{25p^3 q^4}{5p^{-2} q^2 } \right)^{1}$
$= 5p^5 q^2$ → B.
Jika mau cepat, lihat konstantanya. Konstantanya = 25 : 5 = 5.
Hanya opsi B yang konstantanya 5.
$2$. Jika diketahui $^2log\ 3 = x$, maka nilai dari $^8log\ 12$ adalah . . . .
$A.\ \dfrac{-x - 2}{3}$
$B.\ \dfrac{x - 2}{3}$
$C.\ \dfrac{x + 2}{3}$
$D.\ \dfrac{x + 3}{2}$
$E.\ \dfrac{x + 3}{2}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 2.
$^8log\ 12 =\ ^8log\ 4 +\ ^8log\ 3$
$=\ ^{2^3}log\ 2^2 +\ ^{2^3}log\ 3$
$= \dfrac{2}{3}.^2log\ 2 + \dfrac{1}{3}.^2log\ 3$
$= \dfrac{2}{3}.1 + \dfrac{1}{3}.x$
$= \dfrac{2}{3} + \dfrac{x}{3}$
$= \dfrac{2 + x}{3}$ → C.
Klik Sifat-sifat Logaritma untuk mempelajari logaritma.
$3$. Daerah asal dari fungsi $f(x) = \dfrac{\sqrt{2x + 5}}{3x + 2}$, $x ∈ R$ adalah . . . .
$A.\ \{x|x ≠ -\dfrac{5}{2}, x ∈ R\}$
$B.\ \{x|x ≥ \dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$
$C.\ \{x|x ≥ -\dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$
$D.\ \{x|x ≠ -\dfrac{2}{3}, x ∈ R\}$
$E.\ \{x|x ≥ -\dfrac{2}{3}, x ∈ R\}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 3.
Pertama: Yang di dalam tanda akar harus ≥ 0.
$2x + 5 ≥ 0$
$2x ≥ -5$
$x ≥ -\dfrac{5}{2}$
Kedua: Penyebut tidak boleh = 0.
$x ≠ -\dfrac{2}{3}$
Ketiga: $x$ harus bilangan real.
$x ∈ R$
$\{x|x ≥ -\dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$ → C.
$4$. Diketahui $f(x) = 3 - x$ dan $g(x) = x^2 + 2x$. Fungsi komposisi $(g \circ f)(x)$ adalah . . . .
$A.\ (g \circ f)(x) = x^2 - 4x + 15$
$B.\ (g \circ f)(x) = x^2 + 4x + 15$
$C.\ (g \circ f)(x) = x^2 - 4x - 15$
$D.\ (g \circ f)(x) = x^2 - 8x + 15$
$E.\ (g \circ f)(x) = x^2 - 8x - 15$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 4.
$(g \circ f)(x) = g(f(x))$
$= g(3 - x)$
$= (3 - x)^2 + 2(3 - x)$
$= 9 - 6x + x^2 + 6 - 2x$
$= x^2 - 8x + 15$ → D.
$5$. Diketahui $f(x) = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$. Invers dari fungsi $f(x)$ adalah . . . .
$A.\ \dfrac{x + 4}{4x - 1}$, $x ≠ \dfrac{1}{4}$
$B.\ \dfrac{x - 4}{4x + 1}$, $x ≠ -\dfrac{1}{4}$
$C.\ \dfrac{4x - 1}{x + 4}$, $x ≠ -4$
$D.\ \dfrac{4x + 1}{ x - 4}$, $x ≠ 4$
$E.\ \dfrac{4x - 1}{x - 4}$, $x ≠ 4$
Pembahasan soal UN UNBK matematika SMA IPS nomor 5.
$y = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$
$y(x - 4) = 4x + 1$
$xy - 4y = 4x + 1$
$xy - 4x = 4y + 1$
$x(y - 4) = 4y + 1$
$x = \dfrac{4y + 1}{y - 4}$
$f^{-1}(x) = \dfrac{4x + 1}{x - 4},\ x ≠ 4$ → D.
Cara Cepat:
Jika $f(x) = \dfrac{ax + b}{cx + d}$, maka:
$f^{-1}(x) = \dfrac{-dx + b}{cx - a}$
$f^{-1}(x) = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$
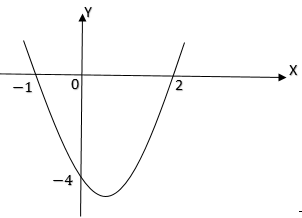
$6$. Perhatikan grafik fungsi kuadrat berikut!
Persamaan fungsi kuadrat
dari grafik di atas adalah . . . .
$A.\ y = x^2 - x - 4$
$B.\ y = x^2 - 2x - 4$
$C.\ y = x^2 + x - 4$
$D.\ y = 2x^2 - 2x - 4$
$E.\ y = 2x^2 + 2x - 4$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 6.
Grafik memotong sumbu $x$ di titik $(-1, 0)$ dan $(2, 0)$ dan melalui titik $(0, -4)$. Persamaan parabola yang memotong sumbu $x$ di titik $(P, 0)\ dan\ (Q, 0)$ adalah:
$y = a(x - P)(x - Q)$
$y = a(x - (-1))(x - 2)$ . . . . (1)
Masukkan titik yang dilalui $(0, -4)$ ke persamaan (1)
$-4 = a(0 + 1)(0 - 2)$
$-4 = - 2a$
$a = 2$
Masukkan kembali $a = 2$ kedalam persamaan (1)
$y = 2(x + 1)(x - 2)$
$y = 2(x^2 - x - 2)$
$y = 2x^2 - 2x - 4$ → D.
$7$. Persamaan kuadrat $x^2 - (a + 2)x + a = 0$ mempunyai akar-akar $p$ dan $q$. Jika $p^2 + q^2 = 28$, maka nilai $a$ positif yang memenuhi adalah . . . .
$A.\ 1$
$B.\ 2$
$C.\ 3$
$D.\ 4$
$E.\ 6$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 7.
$p + q = -\dfrac{b}{a} = \dfrac{-(-(a + 2))}{1} = a + 2$
$pq = \dfrac{c}{a} = \dfrac{a}{1} = a$
$p^2 + q^2 = 28$
$(p + q)^2 - 2pq = 28$
$(a + 2)^2 - 2a = 28$
$a^2 + 4a + 4 - 2a = 28$
$a^2 + 2a - 24 = 0$
$(a + 6)(a - 4) = 0$
$a = -6\ atau\ a = 4$
Karena yang diminta $a$ positif, maka $a = 4$ → D.
$8$. Jika akar-akar persamaan kuadrat $-x^2 + 7x - 6 = 0$ adalah $p$ dan $q$, persamaan kuadrat baru yang akar-akarnya $(p - 2)$ dan $(q - 2)$ adalah . . . .
$A.\ x^2 + 9x - 4 = 0$
$B.\ x^2 + 3x + 4 = 0$
$C.\ -x^2 - 3x - 4 = 0$
$D.\ x^2 + 3x - 4 = 0$
$E.\ -x^2 + 3x + 4 = 0$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 8.
$p + q = -\dfrac{b}{a} = 7$
$pq = \dfrac{c}{a} = 6$
Misalkan persamaan kuadrat yang baru akar-akarnya adalah $α$ dan $β$ dimana $α = p - 2$ dan $β = q - 2$
$α + β = p - 2 + q - 2$
$= p + q - 4$
$= 7 - 4$
$= 3$
$αβ = (p - 2)(q - 2)$
$= pq - 2p - 2q + 4$
$= pq - 2(p + q) + 4$
$= 6 - 2.7 + 4$
$= -4$
Ingat !
Persamaan kuadrat yang akar-akarnya $α$ dan $β$ adalah: $x^2 - (α + β)x + αβ = 0$
$x^2 - 3x - 4 = 0$
karena di opsi tidak ada, kalikan semua dengan negatif!
$-x^2 + 3x + 4 = 0$ → E.
Cara cepat:
$x = p - 2$ → $x + 2 = p$
ganti $x$ dengan $x + 2$
$-(x + 2)^2 + 7(x + 2) - 6 = 0$
$-(x^2 + 4x + 4) + 7x + 14 - 6 = 0$
$-x^2 + 3x + 4 = 0$
$9$. Hasil sensus ekonomi di suatu wilayah pada bisnis transportasi bus, diketahui bahwa jasa sopir ditentukan dari besarnya UMR (Upah Minimum Regional) ditambah dengan hasil kali antara jumlah penumpang dan indeks kepuasan pelanggan. Indeks kepuasan pelanggan di wilayah tersebut senilai dengan 300 kurangnya dari jumlah penumpang per bulan. Jika harga jasa sopir dinyatakan y, jumlah penumpang dinyatakan dalam $x$ dan indeks kepuasan pelanggan dinyatakan z dan besarnya UMR di wilayah tersebut sebesar Rp1.200.000,00, persamaan harga jasa sopir tiap satu bulannya dapat dinyatakan dalam rupiah adalah . . . .
$A.\ y = x^2 + 300x + 1.200.000$
$B.\ y = x^2 - 300x + 1.200.000$
$C.\ y = x^2 + 300x - 1.200.000$
$D.\ y = x^2 - 300x - 1.000.000$
$E.\ y = x^2 + 300x + 1.000.000$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 9.
UMR = 1.200.000
JP (Jumlah Penumpang) = x
IKP (Indeks Kepuasan Pelanggan) = JP - 300 = x - 300.
JS (Jasa sopir) = y
JS = UMR + JP.IKP
JS = UMR + JP.(JP - 300)
$y = 1.200.000 + x(x - 300)$
$y = x^2 - 300x + 1.200.000$ → B.
$10$. Diketahui $p$ dan $q$ memenuhi sistem $\begin{cases}\dfrac{2}{p} + \dfrac{1}{q} = 9\\ \dfrac{1}{p} + \dfrac{3}{q} = 7\end{cases}$. Nilai dari $8p - q$ adalah . . . .
$A.\ 7$
$B.\ \dfrac{5}{2}$
$C.\ 1$
$D.\ -1$
$E.\ -\dfrac{5}{2}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 10.
Misalkan $\dfrac{1}{p} = x$ dan $\dfrac{1}{q} = y$
Persamaan menjadi:
$2x + y = 9$ . . . . (1)
$x + 3y = 7$ . . . . (2)
$2x + y = 9$
$2x + 6y = 14$
------------------------ $-$
$5y = 5$ → $y = 1$
masukkan $y = 1$ ke persamaan (1)
$2x + 1 = 9$
$2x = 8$
$x = 4$
$\dfrac{1}{p} = x$
$\dfrac{1}{p} = 4$
$1 = 4p$
$p = \dfrac{1}{4}$
$\dfrac{1}{q} = y$
$\dfrac{1}{q} = 1$
$q = 1$
$8p - q = 8.\dfrac{1}{4} - 1$
$= 2 - 1$
$= 1$ → C.
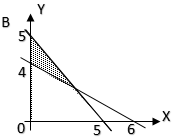
$11$. Grafik berikut yang merupakan penyelesaian sistem pertidaksamaan linier $\begin{cases} 3x + 2y \geqslant 12\\ x + y \leq 5 \\ y\geq 0 \\
x\geqslant 0\end{cases}$ adalah . . . .
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 11.
$(1).\ 3x + 2y ≥ 12$
Titik potong sumbu $X$ → $y = 0 → (4, 0)$
Titik potong sumbu $Y$ → $x = 0 → (0, 6)$
uji titik $(0, 0)$ → $3.0 + 2.0 = 0 < 12$, arsiran menjauhi titik $(0, 0)$
karena yang diminta adalah $≥ 12$
$(2).\ x + y ≤ 5$
Titik potong sumbu $X$ → $y = 0$ → $(5, 0)$
Titik potong sumbu $y$ → $x = 0$ → $(0, 5)$
Uji titik $(0, 0)$ → $0 + 0 = 0 < 5$, arsiran menuju titik $(0, 0)$
karena yang diminta adalah $≤ 5$
(3) $x ≥ 0$ dan $y ≥ 0$ → kuadran I.
Jawab D.
$12$. Seorang wiraswasta kue basah memiliki bahan baku 5 kg tepung, 3 kg gula, dan 1 kg margarin. Untuk membuat kue bika memerlukan 3 kg tepung, 1 kg gula, dan 0,5 kg margarin. Sedangkan untuk kue putri salju memerlukan 2 kg tepung, 2 kg gula, dan 0,5 kg margarin. Jika x menyatakan banyak kue bika dan y menyatakan banyak kue putri salju, model matematika dari masalah tersebut adalah . . . .
A. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
B. x + 2y ≥ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
C. x + 2y ≤ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
D. x + 2y ≥ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
E. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 12.
Periksa tepung: 3x + 2y ≤ 5 → tidak lebih dari 5 kg.
Periksa gula: x + 2y ≤ 3 → tidak lebih dari 3 kg.
Periksa margarin: 0,5x + 0,5y ≤ 1 → tidak lebih dari 1 kg.
x ≥ 0
y ≥ 0
Jawab A.
$13$. Diketahui matriks $A = \begin{pmatrix}a& b\\ 0& 1\end{pmatrix}$, $B = \begin{pmatrix}6 & 1\\ -8 & 7\end{pmatrix}$, $C = \begin{pmatrix}2 & -2\\ 1 & c\end{pmatrix}$, $D = \begin{pmatrix}1 & -1\\ 0 & 2\end{pmatrix}$. Jika $2A + B^T = CD$ dan $B^T$ = transpose B, nilai dari $a + b - c =$ . . . .
$A.\ -8$
$B.\ -6$
$C.\ -4$
$D.\ 6$
$E.\ 8$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 13.
$\begin{pmatrix}2a& 2b\\ 0& 2\end{pmatrix} + \begin{pmatrix}6& -8\\ 1& 7\end{pmatrix} = \begin{pmatrix}2& -6\\ 1& 2c-1\end{pmatrix}$
$\begin{pmatrix}2a + 6& 2b - 8\\ 1& 9\end{pmatrix} = \begin{pmatrix}2& -6\\ 1& 2c-1\end{pmatrix}$
$2a + 6 = 2$ → $2a = -4$ → $a = -2$
$2b - 8 = -6$ → $2b = 2$ → $b = 1$
$2c - 1 = 9$ → $2c = 10$ → $c = 5$
$a + b - c = -2 + 1 - 5 = -6$ → B.
$14$. Diketahui matriks $A = \begin{pmatrix}1& -2\\ -1& 3\end{pmatrix}$ dan matriks $B = \begin{pmatrix}2& 1\\ -1& -1\end{pmatrix}$. Invers dari matriks $AB$ adalah . . . .
$A.\ \begin{pmatrix}4& -3\\ 5& 4\end{pmatrix}$
$B.\ \begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$C.\ \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$
$D.\ \begin{pmatrix}-4& 3\\ -5& 4\end{pmatrix}$
$E.\ \begin{pmatrix}4& 3\\ 5& -4\end{pmatrix}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 14.
$AB = \begin{pmatrix}1& -2\\ -1& 3\end{pmatrix}$$\begin{pmatrix}2& 1\\ -1& -1\end{pmatrix}$
$AB = \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$
$(AB)^{-1} = \dfrac{1}{-16 -(-15)}\begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$(AB)^{-1} = -1\begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$(AB)^{-1} = \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$ → C.
$15$. Seorang ayah menabung uangnya di rumah. Setiap bulan besar tabungan bertambah secara tetap dimulai dari bulan pertama Rp50.000,00, bulan kedua Rp55.000,00, bulan ketiga Rp60.000,00, dan seterusnya. Jumlah tabungan selama 10 bulan adalah . . . .
$A.\ Rp500.000,00$
$B.\ Rp550.000,00$
$C.\ Rp600.000,00$
$D.\ Rp700.000,00$
$E.\ Rp725.000,00$
Pembahasan soal UN UNBK matematika SMA IPS nomor 15.
Deret aritmetika:
$a = 50.000$
$b = 5.000$
$n = 10$
$S_n = \dfrac{n}{2}(2a + (n - 1)b)$
$S_n = \dfrac{10}{2}(2.(50.000) + (10 - 1)5.000)$
$S_n = 5(145.000)$
$S_n = 725.000,00$ → E.
$16.\displaystyle \lim_{x \to 3} \dfrac{x^2-x-6}{x^2-x-20} =$ . . . .
$A.\ -2$
$B.\ -1$
$C.\ 0$
$D.\ 1$
$E.\ ∞$
Pembahasan soal UN UNBK matematika SMA IPS nomor 16.
Karena bukan limit $\dfrac{0}{0}$, langsung substitusikan $x = 3$ ke dalam persamaan.
$\displaystyle \lim_{x \to 3}\dfrac{x^2-x-6}{x^2-x-20}$
$= \dfrac{3^2-3-6}{3^2-3-20}$
$= \dfrac{0}{-14}$
$= 0$
$17.\ \displaystyle \lim_{x \to 4}\dfrac{x^2-16}{x^2-x-12} =$ . . . .
$A.\ 4$
$B.\ 2$
$C.\ 1$
$D.\ \dfrac{5}{7}$
$E.\ \dfrac{8}{7}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 17.
Karena $\dfrac{0}{0}$, sederhanakan dengan memfaktorkan.
$\displaystyle \lim_{x \to 4}\dfrac{x^2-16}{x^2-x-12}$
$= \displaystyle \lim_{x \to 4}\dfrac{(x + 4)(x - 4)}{(x - 4)(x + 3)}$
$= \displaystyle \lim_{x \to 4}\dfrac{(x + 4)}{(x + 3)}$
$= \dfrac{(4 + 4)}{(4 + 3)}$
$= \dfrac{8}{7}$ → E.
Cara cepat:
Pakai aturan L'Hopital yaitu dengan menurunkan atas dan bawah.
$\displaystyle \dfrac{x^2-16}{x^2-x-12}$
$= \displaystyle \dfrac{2x}{2x - 1}$
$= \dfrac{2.4}{2.4 - 1}$
$= \dfrac{8}{7}$
$18$. Turunan pertama fungsi $f(x) = (5x - 3)^3$ adalah . . . .
$A.\ f'(x) = 3((5x - 3)^2$
$B.\ f'(x) = 5((5x - 3)^2$
$C.\ f'(x) = 8((5x - 3)^2$
$D.\ f'(x) = 15((5x - 3)^2$
$E.\ f'(x) = 45((5x - 3)^2$
Pembahasan soal UN UNBK matematika SMA IPS nomor 18.
Jika $f(x) = [g(x)]^n$ maka $f'(x) = n[g(x)]^{n-1}.g'(x)$
$f(x) = (5x - 3)^3$
$f'(x) = 3(5x - 3)^2.5$
$f'(x) = 15(5x - 3)^2$ → D.
$19$. Grafik fungsi $f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 6x + 2$ turun pada interval . . . .
$A.\ -2 < x < 3$
$B.\ -3 < x < 2$
$C.\ 2 < x < 3$
$D.\ x < -2\ atau\ x > 3$
$E.\ x < -3\ atau\ x > 2$
Pembahasan soal UN UNBK matematika SMA IPS nomor 19.
Fungsi naik jika $f'(x) > 0$
Fungsi turun jika $f'(x) < 0$
$f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 6x + 2$
$f'(x) = x^2 - x - 6 < 0$
$(x + 2)(x - 3) < 0$
$-2 < x < 3$ → A.
$20.\ \displaystyle \int_{0}^{2}x(3x + 5)dx =$ . . . .
$A.\ 18$
$B.\ 16$
$C.\ 15$
$D.\ 10$
$E.\ 6$
Pembahasan soal UN UNBK matematika SMA IPS nomor 20.
Ingat !
$\displaystyle \int ax^ndx = \frac{a}{n + 1}x^{n + 1} + c$
$\displaystyle \int_{0}^{2}x(3x + 5)dx$
$= \displaystyle \int_{0}^{2}(3x^2 + 5x)dx$
$= (x^3 + \dfrac{5}{2}x^2)|_{0}^{2}$
$= 2^3 + \dfrac{5}{2}.2^2 - (0^3 + \dfrac{5}{2}.0^2)$
$= 8 + 10$
$= 18$ → A.
$21.\ \displaystyle \int_{-1}^{2}(6x^2 + 8x)dx =$ . . . .
$A.\ 24$
$B.\ 26$
$C.\ 28$
$D.\ 30$
$E.\ 32$
Pembahasan soal UN UNBK matematika SMA IPS nomor 21.
$\displaystyle \int_{-1}^{2}(6x^2 + 8x)dx = (2x^3 + 4x^2)|_{-1}^{2}$
$= (2.2^3 + 4.2^2 - (2.(-1)^3 + 4(-1)^2)$
$= 16 + 16 - (-2 + 4)$
$= 30$ → D.
$22$. Diketahui segitiga $ABC$ siku-siku di C dan $sin A = \dfrac{2}{7}$. Nilai $tan\ B$ adalah . . . .
$A.\ \dfrac{3}{5}\sqrt{5}$
$B.\ \dfrac{4}{5}\sqrt{5}$
$C.\ \dfrac{2}{3}\sqrt{5}$
$D.\ \dfrac{3}{5}\sqrt{5}$
$E.\ \dfrac{1}{3}\sqrt{5}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 22.
Perhatikan gambar diatas.
Jika $sin\ A = \dfrac{2}{7}$, maka sisi depan sudut $A = 2$ dan sisi miring $= 7$. Terlihat dengan jelas bahwa $tan\ B = \dfrac{3}{2}\sqrt{5}$ → A.
$23$. Nilai dari $cos 210^{\circ}.sin 330^{\circ} - cos 60^{\circ}$ adalah . . . .
$A.\ -\dfrac{1}{4}(2 - \sqrt{3})$
$B.\ -\dfrac{3}{4}(2 - \sqrt{3})$
$C.\ 0$
$D.\ \dfrac{1}{4}(2 - \sqrt{3})$
$E.\ \dfrac{3}{4}(2 - \sqrt{3})$
Pembahasan soal UN UNBK matematika SMA IPS nomor 23.
$cos 210^{\circ}.sin 330^{\circ} - cos 60^{\circ}$
$= cos (180 + 30)^{\circ}.sin (360 - 30)^{\circ} - cos 60^{\circ}$
$= -cos 30^{\circ}.(-sin 30^{\circ}) - cos 60^{\circ}$
$= -\dfrac{1}{2}\sqrt{3}.(-\dfrac{1}{2}) - \dfrac{1}{2}$
$= \dfrac{1}{4}\sqrt{3} - \dfrac{1}{2}$
$= \dfrac{1}{4}(\sqrt{3} - 2)$
$= -\dfrac{1}{4}(\sqrt{3} + 2)$ → A.
$24$. Sebuah tangga menyandar pada dinding dengan kemiringan $60^{\circ}$. Jika panjang tangga 5 meter, jarak dari kaki tangga ke dinding adalah . . . .
$A.\ \dfrac{5}{2}\ meter$
$B.\ \dfrac{5}{2}\sqrt{2}\ meter$
$C.\ \dfrac{5}{2}\sqrt{3}\ meter$
$D.\ 5\sqrt{2}\ meter$
$E.\ 5\sqrt{3}\ meter$
Pembahasan soal UN UNBK matematika SMA IPS nomor 24.
Perhatikan gambar dibawah!
$cos 60^{\circ} = \dfrac{x}{5}$
$\dfrac{1}{2} = \dfrac{x}{5}$
$x = \dfrac{5}{2}$ → A.
$25.\ \dfrac{sin\ x}{tan^2\ x} =$ . . . .
$A.\ sin\ x.tan\ x$
$B.\ sin\ x.cot\ x$
$C.\ cos\ x.tan\ x$
$D.\ cos\ x.cot\ x$
$E.\ sec\ x.tan\ x$
Pembahasan soal UN UNBK matematika SMA IPS nomor 25.
$\dfrac{sin\ x}{tan^2\ x} = \dfrac{sin\ x}{\dfrac{sin^2\ x}{cos^2\ x}}$
$= \dfrac{sin\ x.cos^2\ x}{sin^2\ x}$
$= \dfrac{cos^2\ x}{sin\ x}$
$= \dfrac{cos\ x}{sin\ x}.cos\ x$
$= cot\ x.cos\ x$ → D.
$26$. Besar sudut antara ruas garis AG dan bidang EFGH pada kubus ABCD.EFGH adalah $\alpha$. Nilai $cos \alpha$ adalah . . . .
$A.\ \dfrac{1}{3}\sqrt{3}$
$B.\ \dfrac{1}{2}\sqrt{3}$
$C.\ \dfrac{1}{3}\sqrt{6}$
$D.\ \dfrac{1}{2}\sqrt{6}$
$E.\ \dfrac{1}{3}\sqrt{3}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 26.
Perhatikan gambar di atas!
Panjang $AG = a\sqrt{3}$ → diagonal ruang.
Panjang $EG = a\sqrt{2}$ → diagonal sisi.
$cos\ \alpha = \dfrac{EG}{AG}$
$= \dfrac{a\sqrt{2}}{a\sqrt{3}}$
$= \dfrac{\sqrt{2}}{\sqrt{3}}$
$= \dfrac{1}{3}\sqrt{6}$ → C.
$27$. Berikut ini adalah pernyataan-pernyataan tentang kubus ABCD.EFGH dengan P, Q, R berturut-turut titik-titik tengah rusuk AE, CG, dan DH.
(1) Ruas garis QE dan RF berpotongan
(2) Ruas garis QB dan PB tegak lurus
(3) Ruas garis QB dan HP tidak sejajar
(4) Segitiga PDQ samakaki
Pernyataan yang benar adalah . . . .
A. (1) dan (2)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
E. (3) dan (4)
Pembahasan soal UN UNBK matematika SMA IPS nomor 27.
Perhatikan gambar di atas!
$\bullet$ Ruas garis QE dan RF pasti berpotongan.
$\bullet$ Ruas garis QB dan PB tidak tegak lurus.
Panjang PQ = AC = $a\sqrt{2}$. Karena segitiga
ABC siku-siku di B, tidak mungkin segitiga PBQ
siku-siku di B, karena PB tidak sama dengan AC.
$\bullet$ Ruas garis QB dan HP adalah sejajar.
$\bullet$ Segitiga PDQ sama kaki. Panjang DP sama dengan DQ.
Jadi jawab yang benar adalah (1) dan (4) → B.
$28$. Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Titik P terletak di tengah diagonal sisi AC. Jarak dari titik C ke garis GP adalah . . . .
$A.\ 4\sqrt{3}$
$B.\ 4\sqrt{2}$
$C.\ 3\sqrt{3}$
$D.\ 3\sqrt{2}$
$E.\ 2\sqrt{3}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 28.
Perhatikan gambar di atas!
$AC = 6\sqrt{2}$ → $PC = \dfrac12AC = 3\sqrt{2}$
$PG^2 = PC^2 + CG^2$
$PG^2 = (3\sqrt{2})^2 + 6^2$
$PG^2 = 18 + 36$
$PG = 3\sqrt{6}$
$CQ = \dfrac{PC.CG}{PG}$
$CQ = \dfrac{3\sqrt{2}.6}{3\sqrt{6}}$
$CQ = 2\sqrt{3}$ → E.
Cara cepat:
Untuk soal yang sejenis, misalnya jarak antara titik A ke garis EP, jarak antara D ke garis HP, dan lain-lain, gunakan RUMUS $R = \dfrac{1}{3}a\sqrt{3}$
R → jarak, dan a panjang rusuk kubus.
Dari soal: $R = \dfrac{1}{3}.6.\sqrt{3} = 2\sqrt{3}$.
$29$. Data nilai ujian matematika di suatu kelas disajikan pada tabel distribusi frekwensi kumulatif "kurang dari". Banyak siswa yang memperoleh nilai 40 - 59 adalah . . . .
$A.\ 7$
$B.\ 8$
$C.\ 10$
$D.\ 18$
$E.\ 26$
Pembahasan soal UN UNBK matematika SMA IPS nomor 29.
Tabel distribusi frekwensinya adalah seperti di bawah.
Berarti banyak siswa yang memperoleh nilai
40 - 59 adalah 8 orang. → B.
$30$. Tabel berat badan sekelompok siswa.
Modus dari berat badan siswa adalah . . . .
$A.\ 49,06\ kg$
$B.\ 50,20\ kg$
$C.\ 50,40\ kg$
$D.\ 51,33\ kg$
$E.\ 51,83\ kg$
Pembahasan soal UN UNBK matematika SMA IPS nomor 30.
Kelas modus adalah $(49 - 54)$ → $M_1 = 49 - 0,5 = 48,5$
$d_1 = 14 - 10 = 4$
$d_2 = 14 - 8 = 6$
Panjang kelas $c = 36,5 - 30,5 = 6$
$M_o = M_1 + \dfrac{d_1}{d_1 + d_2}.c$
$M_o = 48,5 + \dfrac{4}{4 + 6}.6$
$M_o = 48,5 + \dfrac{4}{10}.6$
$M_o = 48,5 + 2,4$
$M_o = 50,9$ → Tidak ada jawaban.
$31$. Perhatikan berat badan dari kelompok siswa!
Kuartil bawah dari berat badan siswa adalah . . . .
$A.\ 37,00\ kg$
$B.\ 42,00\ kg$
$C.\ 45,50\ kg$
$D.\ 53,25\ kg$
$E.\ 53,78\ kg$
Pembahasan soal UN UNBK matematika SMA IPS nomor 31.
Kuartil bawah: $n = \sum f = 40$
$\dfrac{1}{4}n = \dfrac{1}{4}.40 = 10$
Berarti kuartil bawah terletak pada kelas (40 - 44)
$L_1 = 40 - 0,5 = 39,5$
$f^1 = 7$ → jumlah frekwensi yang ada di atas kelas
kuartil bawah. Dalam soal ini 3 + 4 = 7.
$f_1 = 6$ → Frekwensi kelas kuartil bawah.
Panjang kelas $c = 34,5 - 29,5 = 5$
$Q_1 = L_1 + \dfrac{\dfrac{1}{4}n - f^1}{f_1}.c$
$Q_1 = 39,5 + \dfrac{\dfrac{1}{4}.40 - 7}{6}.5$
$Q_1 = 39,5 + \dfrac{1}{2}.5$
$Q_1 = 39,5 + 2,5$
$Q_1 = 42,00$ → B.
$32$. Simpangan rata-rata dari data 6,5,7,5,6,8,7,6,6,7,4,5
adalah . . . .
$A.\ \dfrac{7}{3}$
$B.\ \dfrac{5}{3}$
$C.\ \dfrac{7}{5}$
$D.\ \dfrac{3}{5}$
$E.\ \dfrac{5}{6}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 32.
$\overline{x} = \dfrac{4 + 3.5 + 4.6 + 3.7 + 8}{12}$
$\overline{x} = \dfrac{72}{12} = 6$
$SR = \dfrac{\displaystyle \sum_{i=1}^{n}|x_i - \overline{x}|}{n}$
$= \dfrac{|4 - 6| + 3.|5 - 6| + 4.|6 - 6| + 3.|6 - 7| + |8 - 6|}{12}$
$= \dfrac{2 + 3 + 0 + 3 + 2}{12}$
$= \dfrac{10}{12}$
$= \dfrac{5}{6}$
jawab: E.
$33$. Dari 8 orang calon termasuk Joko akan dipilih 4 orang sebagai pengurus kelas, yaitu sebagai ketua, wakil ketua, sekretaris, dan bendahara. Banyaknya susunan pengurus kelas yang mungkin terjadi, jika Joko harus menjadi ketua kelas adalah . . . .
$A.\ 35\ susunan$
$B.\ 56\ susunan$
$C.\ 210\ susunan$
$D.\ 336\ susunan$
$E.\ 1680\ susunan$
Pembahasan soal UN UNBK matematika SMA IPS nomor 33.
Karena Joko sudah dipastikan menduduki posisi ketua kelas, maka yang harus dipilih adalah posisi wakil ketua kelas, sekretaris, dan bendahara yang harus dipilih dari 7 orang sisa.
Banyak cara $=\ _{4}^{7}\textrm{P}$
$= \dfrac{7!}{(7-3)!}$
$= \dfrac{7!}{4!}$
$= \dfrac{7.6.5.4!}{4!}$
$= 7.6.5$
$= 210$ susunan → C.
$34$. Seorang ibu akan memilih 4 bunga dari 8 macam bunga. Banyak cara yang mungkin untuk memilih bunga tersebut adalah . . . .
$A.\ 24\ cara$
$B.\ 32\ cara$
$C.\ 70\ cara$
$D.\ 1.680\ cara$
$E.\ 40.320\ cara$
Pembahasan soal UN UNBK matematika SMA IPS nomor 34.
Banyak cara = $_{4}^{8}\textrm{C}$
$= \dfrac{8!}{(8-4)!.4!}$
$= \dfrac{8!}{4!.4!}$
$= \dfrac{8.7.6.5.4!}{4.3.2.1.4!}$
$= \dfrac{8.7.6.5}{4.3.2.1}$
$= 70$ cara → C.
$35$. Sebuah dadu dan sebuah koin dilambungkan satu kali secara bersama-sama. Peluang muncul gambar pada koin dan bilangan genap pada dadu adalah . . . .
$A.\ \dfrac14$
$B.\ \dfrac12$
$C.\ \dfrac23$
$D.\ \dfrac34$
$E.\ \dfrac67$
Pembahasan soal UN UNBK matematika SMA IPS nomor 35.
Perhatikan tabel di atas!
Banyak ruang sampel $n(S) = 12$
Gambar pada koin dan bilangan genap pada dadu ada 3 anggota → $n(A) = 3$
$P(A) = \dfrac{n(A)}{n(S)} = \dfrac{3}{12} = \dfrac{1}{4}$ → A.
$36$. Dari 7 kartu yang diberi huruf S, U, C, I, P, T, O diambil sebuah kartu secara acak. Jika pengambilan dilakukan sebanyak 70 kali dengan pengembalian, frekwensi harapan yang terambil huruf vokal adalah . . . .
$A.\ 20\ kali$
$B.\ 30\ kali$
$C.\ 40\ kali$
$D.\ 50\ kali$
$E.\ 60\ kali$
Pembahasan soal UN UNBK matematika SMA IPS nomor 36.
$n(S) = 7$
$n(A) = 3$
$P(A) = \dfrac{n(A)}{n(S)}$
$P(A) = \dfrac{3}{7}$
$F_h = P(A).BP$ → BP = Banyak Percobaan
$F_h = \dfrac{3}{7}.70$
$F_h = 30$ kali → B.
ISIAN
$37$. Pak Amir membeli 10 kg beras dan 5 kg gula dengan harga Rp185.000,00. Di toko yang sama Pak Budi membeli 15 kg beras dan 5 kg gula dengan harga Rp240.000,00. Harga 1 kg beras di toko tersebut adalah . . . . rupiah.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 37.
misalkan jumlah beras = x
misalkan jumlah gula = y
10x + 5y = 185.000 → 2x + y = 37.000 . . . . (1)
15x + 5y = 240.000 → 3x + y = 48.000 . . . . (2)
Eliminasi persamaan (1) dan (2)
2x + y = 37.000
3x + y = 48.000
----------------------------- $-$
x = 11.000
jadi harga 1 kg beras = Rp11.000,00. → 11.000
$38$. Setiap 3 tahun jumlah pengguna telepon genggam di kota Rayland bertambah 2 kali lipat jumlah semula. Jika pada tahun 2015 pengguna telepon genggam di sana adalah 28.800 orang, jumlah pengguna telepon genggam pada tahun 2006 di kota tersebut adalah . . . . orang.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 38.
Deret Geometri:
$r = 2$
$n = \dfrac{2015 - 2006}{3} + 1 = \dfrac{9}{3} + 1 = 4$
$U_n = 28.800$
$a =\ .\ .\ .\ .\ ?$
$U_n = ar^{n - 1}$
$28.800 = a.2^{4 - 1}$
$28.800 = 8a$
$a = \dfrac{28.800}{8}$
$a = 3.600$.
jadi banyak pengguna telepon genggam pada tahun
2006 adalah 3.600 orang. → 3.600
$39$. Biaya produksi setiap P barang adalah $(50P + P^2)$ ribu rupiah. Harga jual setiap unit barang tersebut adalah 100 ribu rupiah. Banyaknya unit yang dijual agar keuntungan maksimum adalah . . . . unit.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 39.
Harga jual P unit = $100P$ (dalam ribu)
Biaya produksi P unit $= 50P + P^2$ (dalam ribu)
Misalkan keuntungan adalah K.
$K(P) = 100P - (50P + P^2)$
$K(P) = -P^2 + 50P$
$K'(P) = -2P + 50 = 0$
$2P = 50$
$P = 25$
Banyak unit yang dijual = 25 unit → 25
$40$. Dari angka 1,2,3,4,5,6 dan 8 akan dibentuk bilangan genap yang terdiri atas 3 angka berlainan. Banyaknya kemungkinan bilangan berbeda yang dapat dibentuk adalah . . . .
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 40.
Banyaknya bilangan genap = $6.5.4 = 120$. → 120
SHARE THIS POST
www.maretong.com
Selamat Berjuang!
$1$. Bentuk sederhana dari $\left(\dfrac{5p^{-2} q^2}{25p^3 q^4} \right)^{-1}$ adalah . . . .
$A.\ 25p^5q^2$
$B.\ 5p^5q^2$
$C.\ p^5q^2$
$D.\ \dfrac{1}{5}p^5q^2$
$E.\ \dfrac{1}{25}p^5q^2$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 1.
Ingat !
$\left(\dfrac{a}{b}\right)^{-n} = \left(\dfrac{b}{a}\right)^{n}$
$\left(\dfrac{5p^{-2} q^2}{25p^3 q^4} \right)^{-1} = \left(\dfrac{25p^3 q^4}{5p^{-2} q^2 } \right)^{1}$
$= 5p^5 q^2$ → B.
Jika mau cepat, lihat konstantanya. Konstantanya = 25 : 5 = 5.
Hanya opsi B yang konstantanya 5.
$2$. Jika diketahui $^2log\ 3 = x$, maka nilai dari $^8log\ 12$ adalah . . . .
$A.\ \dfrac{-x - 2}{3}$
$B.\ \dfrac{x - 2}{3}$
$C.\ \dfrac{x + 2}{3}$
$D.\ \dfrac{x + 3}{2}$
$E.\ \dfrac{x + 3}{2}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 2.
$^8log\ 12 =\ ^8log\ 4 +\ ^8log\ 3$
$=\ ^{2^3}log\ 2^2 +\ ^{2^3}log\ 3$
$= \dfrac{2}{3}.^2log\ 2 + \dfrac{1}{3}.^2log\ 3$
$= \dfrac{2}{3}.1 + \dfrac{1}{3}.x$
$= \dfrac{2}{3} + \dfrac{x}{3}$
$= \dfrac{2 + x}{3}$ → C.
Klik Sifat-sifat Logaritma untuk mempelajari logaritma.
$3$. Daerah asal dari fungsi $f(x) = \dfrac{\sqrt{2x + 5}}{3x + 2}$, $x ∈ R$ adalah . . . .
$A.\ \{x|x ≠ -\dfrac{5}{2}, x ∈ R\}$
$B.\ \{x|x ≥ \dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$
$C.\ \{x|x ≥ -\dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$
$D.\ \{x|x ≠ -\dfrac{2}{3}, x ∈ R\}$
$E.\ \{x|x ≥ -\dfrac{2}{3}, x ∈ R\}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 3.
Pertama: Yang di dalam tanda akar harus ≥ 0.
$2x + 5 ≥ 0$
$2x ≥ -5$
$x ≥ -\dfrac{5}{2}$
Kedua: Penyebut tidak boleh = 0.
$x ≠ -\dfrac{2}{3}$
Ketiga: $x$ harus bilangan real.
$x ∈ R$
$\{x|x ≥ -\dfrac{5}{2}, x ≠ -\dfrac{2}{3}, x ∈ R\}$ → C.
$4$. Diketahui $f(x) = 3 - x$ dan $g(x) = x^2 + 2x$. Fungsi komposisi $(g \circ f)(x)$ adalah . . . .
$A.\ (g \circ f)(x) = x^2 - 4x + 15$
$B.\ (g \circ f)(x) = x^2 + 4x + 15$
$C.\ (g \circ f)(x) = x^2 - 4x - 15$
$D.\ (g \circ f)(x) = x^2 - 8x + 15$
$E.\ (g \circ f)(x) = x^2 - 8x - 15$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 4.
$(g \circ f)(x) = g(f(x))$
$= g(3 - x)$
$= (3 - x)^2 + 2(3 - x)$
$= 9 - 6x + x^2 + 6 - 2x$
$= x^2 - 8x + 15$ → D.
$5$. Diketahui $f(x) = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$. Invers dari fungsi $f(x)$ adalah . . . .
$A.\ \dfrac{x + 4}{4x - 1}$, $x ≠ \dfrac{1}{4}$
$B.\ \dfrac{x - 4}{4x + 1}$, $x ≠ -\dfrac{1}{4}$
$C.\ \dfrac{4x - 1}{x + 4}$, $x ≠ -4$
$D.\ \dfrac{4x + 1}{ x - 4}$, $x ≠ 4$
$E.\ \dfrac{4x - 1}{x - 4}$, $x ≠ 4$
Pembahasan soal UN UNBK matematika SMA IPS nomor 5.
$y = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$
$y(x - 4) = 4x + 1$
$xy - 4y = 4x + 1$
$xy - 4x = 4y + 1$
$x(y - 4) = 4y + 1$
$x = \dfrac{4y + 1}{y - 4}$
$f^{-1}(x) = \dfrac{4x + 1}{x - 4},\ x ≠ 4$ → D.
Cara Cepat:
Jika $f(x) = \dfrac{ax + b}{cx + d}$, maka:
$f^{-1}(x) = \dfrac{-dx + b}{cx - a}$
$f^{-1}(x) = \dfrac{4x + 1}{x - 4}$, $x ≠ 4$
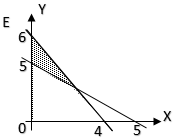
$6$. Perhatikan grafik fungsi kuadrat berikut!
Persamaan fungsi kuadrat
dari grafik di atas adalah . . . .
$A.\ y = x^2 - x - 4$
$B.\ y = x^2 - 2x - 4$
$C.\ y = x^2 + x - 4$
$D.\ y = 2x^2 - 2x - 4$
$E.\ y = 2x^2 + 2x - 4$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 6.
Grafik memotong sumbu $x$ di titik $(-1, 0)$ dan $(2, 0)$ dan melalui titik $(0, -4)$. Persamaan parabola yang memotong sumbu $x$ di titik $(P, 0)\ dan\ (Q, 0)$ adalah:
$y = a(x - P)(x - Q)$
$y = a(x - (-1))(x - 2)$ . . . . (1)
Masukkan titik yang dilalui $(0, -4)$ ke persamaan (1)
$-4 = a(0 + 1)(0 - 2)$
$-4 = - 2a$
$a = 2$
Masukkan kembali $a = 2$ kedalam persamaan (1)
$y = 2(x + 1)(x - 2)$
$y = 2(x^2 - x - 2)$
$y = 2x^2 - 2x - 4$ → D.
$7$. Persamaan kuadrat $x^2 - (a + 2)x + a = 0$ mempunyai akar-akar $p$ dan $q$. Jika $p^2 + q^2 = 28$, maka nilai $a$ positif yang memenuhi adalah . . . .
$A.\ 1$
$B.\ 2$
$C.\ 3$
$D.\ 4$
$E.\ 6$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 7.
$p + q = -\dfrac{b}{a} = \dfrac{-(-(a + 2))}{1} = a + 2$
$pq = \dfrac{c}{a} = \dfrac{a}{1} = a$
$p^2 + q^2 = 28$
$(p + q)^2 - 2pq = 28$
$(a + 2)^2 - 2a = 28$
$a^2 + 4a + 4 - 2a = 28$
$a^2 + 2a - 24 = 0$
$(a + 6)(a - 4) = 0$
$a = -6\ atau\ a = 4$
Karena yang diminta $a$ positif, maka $a = 4$ → D.
$8$. Jika akar-akar persamaan kuadrat $-x^2 + 7x - 6 = 0$ adalah $p$ dan $q$, persamaan kuadrat baru yang akar-akarnya $(p - 2)$ dan $(q - 2)$ adalah . . . .
$A.\ x^2 + 9x - 4 = 0$
$B.\ x^2 + 3x + 4 = 0$
$C.\ -x^2 - 3x - 4 = 0$
$D.\ x^2 + 3x - 4 = 0$
$E.\ -x^2 + 3x + 4 = 0$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 8.
$p + q = -\dfrac{b}{a} = 7$
$pq = \dfrac{c}{a} = 6$
Misalkan persamaan kuadrat yang baru akar-akarnya adalah $α$ dan $β$ dimana $α = p - 2$ dan $β = q - 2$
$α + β = p - 2 + q - 2$
$= p + q - 4$
$= 7 - 4$
$= 3$
$αβ = (p - 2)(q - 2)$
$= pq - 2p - 2q + 4$
$= pq - 2(p + q) + 4$
$= 6 - 2.7 + 4$
$= -4$
Ingat !
Persamaan kuadrat yang akar-akarnya $α$ dan $β$ adalah: $x^2 - (α + β)x + αβ = 0$
$x^2 - 3x - 4 = 0$
karena di opsi tidak ada, kalikan semua dengan negatif!
$-x^2 + 3x + 4 = 0$ → E.
Cara cepat:
$x = p - 2$ → $x + 2 = p$
ganti $x$ dengan $x + 2$
$-(x + 2)^2 + 7(x + 2) - 6 = 0$
$-(x^2 + 4x + 4) + 7x + 14 - 6 = 0$
$-x^2 + 3x + 4 = 0$
$9$. Hasil sensus ekonomi di suatu wilayah pada bisnis transportasi bus, diketahui bahwa jasa sopir ditentukan dari besarnya UMR (Upah Minimum Regional) ditambah dengan hasil kali antara jumlah penumpang dan indeks kepuasan pelanggan. Indeks kepuasan pelanggan di wilayah tersebut senilai dengan 300 kurangnya dari jumlah penumpang per bulan. Jika harga jasa sopir dinyatakan y, jumlah penumpang dinyatakan dalam $x$ dan indeks kepuasan pelanggan dinyatakan z dan besarnya UMR di wilayah tersebut sebesar Rp1.200.000,00, persamaan harga jasa sopir tiap satu bulannya dapat dinyatakan dalam rupiah adalah . . . .
$A.\ y = x^2 + 300x + 1.200.000$
$B.\ y = x^2 - 300x + 1.200.000$
$C.\ y = x^2 + 300x - 1.200.000$
$D.\ y = x^2 - 300x - 1.000.000$
$E.\ y = x^2 + 300x + 1.000.000$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 9.
UMR = 1.200.000
JP (Jumlah Penumpang) = x
IKP (Indeks Kepuasan Pelanggan) = JP - 300 = x - 300.
JS (Jasa sopir) = y
JS = UMR + JP.IKP
JS = UMR + JP.(JP - 300)
$y = 1.200.000 + x(x - 300)$
$y = x^2 - 300x + 1.200.000$ → B.
$10$. Diketahui $p$ dan $q$ memenuhi sistem $\begin{cases}\dfrac{2}{p} + \dfrac{1}{q} = 9\\ \dfrac{1}{p} + \dfrac{3}{q} = 7\end{cases}$. Nilai dari $8p - q$ adalah . . . .
$A.\ 7$
$B.\ \dfrac{5}{2}$
$C.\ 1$
$D.\ -1$
$E.\ -\dfrac{5}{2}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 10.
Misalkan $\dfrac{1}{p} = x$ dan $\dfrac{1}{q} = y$
Persamaan menjadi:
$2x + y = 9$ . . . . (1)
$x + 3y = 7$ . . . . (2)
$2x + y = 9$
$2x + 6y = 14$
------------------------ $-$
$5y = 5$ → $y = 1$
masukkan $y = 1$ ke persamaan (1)
$2x + 1 = 9$
$2x = 8$
$x = 4$
$\dfrac{1}{p} = x$
$\dfrac{1}{p} = 4$
$1 = 4p$
$p = \dfrac{1}{4}$
$\dfrac{1}{q} = y$
$\dfrac{1}{q} = 1$
$q = 1$
$8p - q = 8.\dfrac{1}{4} - 1$
$= 2 - 1$
$= 1$ → C.
$11$. Grafik berikut yang merupakan penyelesaian sistem pertidaksamaan linier $\begin{cases} 3x + 2y \geqslant 12\\ x + y \leq 5 \\ y\geq 0 \\
x\geqslant 0\end{cases}$ adalah . . . .
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 11.
$(1).\ 3x + 2y ≥ 12$
Titik potong sumbu $X$ → $y = 0 → (4, 0)$
Titik potong sumbu $Y$ → $x = 0 → (0, 6)$
uji titik $(0, 0)$ → $3.0 + 2.0 = 0 < 12$, arsiran menjauhi titik $(0, 0)$
karena yang diminta adalah $≥ 12$
$(2).\ x + y ≤ 5$
Titik potong sumbu $X$ → $y = 0$ → $(5, 0)$
Titik potong sumbu $y$ → $x = 0$ → $(0, 5)$
Uji titik $(0, 0)$ → $0 + 0 = 0 < 5$, arsiran menuju titik $(0, 0)$
karena yang diminta adalah $≤ 5$
(3) $x ≥ 0$ dan $y ≥ 0$ → kuadran I.
Jawab D.
$12$. Seorang wiraswasta kue basah memiliki bahan baku 5 kg tepung, 3 kg gula, dan 1 kg margarin. Untuk membuat kue bika memerlukan 3 kg tepung, 1 kg gula, dan 0,5 kg margarin. Sedangkan untuk kue putri salju memerlukan 2 kg tepung, 2 kg gula, dan 0,5 kg margarin. Jika x menyatakan banyak kue bika dan y menyatakan banyak kue putri salju, model matematika dari masalah tersebut adalah . . . .
A. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
B. x + 2y ≥ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
C. x + 2y ≤ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
D. x + 2y ≥ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
E. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 12.
Periksa tepung: 3x + 2y ≤ 5 → tidak lebih dari 5 kg.
Periksa gula: x + 2y ≤ 3 → tidak lebih dari 3 kg.
Periksa margarin: 0,5x + 0,5y ≤ 1 → tidak lebih dari 1 kg.
x ≥ 0
y ≥ 0
Jawab A.
$13$. Diketahui matriks $A = \begin{pmatrix}a& b\\ 0& 1\end{pmatrix}$, $B = \begin{pmatrix}6 & 1\\ -8 & 7\end{pmatrix}$, $C = \begin{pmatrix}2 & -2\\ 1 & c\end{pmatrix}$, $D = \begin{pmatrix}1 & -1\\ 0 & 2\end{pmatrix}$. Jika $2A + B^T = CD$ dan $B^T$ = transpose B, nilai dari $a + b - c =$ . . . .
$A.\ -8$
$B.\ -6$
$C.\ -4$
$D.\ 6$
$E.\ 8$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 13.
$\begin{pmatrix}2a& 2b\\ 0& 2\end{pmatrix} + \begin{pmatrix}6& -8\\ 1& 7\end{pmatrix} = \begin{pmatrix}2& -6\\ 1& 2c-1\end{pmatrix}$
$\begin{pmatrix}2a + 6& 2b - 8\\ 1& 9\end{pmatrix} = \begin{pmatrix}2& -6\\ 1& 2c-1\end{pmatrix}$
$2a + 6 = 2$ → $2a = -4$ → $a = -2$
$2b - 8 = -6$ → $2b = 2$ → $b = 1$
$2c - 1 = 9$ → $2c = 10$ → $c = 5$
$a + b - c = -2 + 1 - 5 = -6$ → B.
$14$. Diketahui matriks $A = \begin{pmatrix}1& -2\\ -1& 3\end{pmatrix}$ dan matriks $B = \begin{pmatrix}2& 1\\ -1& -1\end{pmatrix}$. Invers dari matriks $AB$ adalah . . . .
$A.\ \begin{pmatrix}4& -3\\ 5& 4\end{pmatrix}$
$B.\ \begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$C.\ \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$
$D.\ \begin{pmatrix}-4& 3\\ -5& 4\end{pmatrix}$
$E.\ \begin{pmatrix}4& 3\\ 5& -4\end{pmatrix}$
Pembahasan soal UN UNBK matematika SMA IPS 2018 nomor 14.
$AB = \begin{pmatrix}1& -2\\ -1& 3\end{pmatrix}$$\begin{pmatrix}2& 1\\ -1& -1\end{pmatrix}$
$AB = \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$
$(AB)^{-1} = \dfrac{1}{-16 -(-15)}\begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$(AB)^{-1} = -1\begin{pmatrix}-4& -3\\ 5& 4\end{pmatrix}$
$(AB)^{-1} = \begin{pmatrix}4& 3\\ -5& -4\end{pmatrix}$ → C.
$15$. Seorang ayah menabung uangnya di rumah. Setiap bulan besar tabungan bertambah secara tetap dimulai dari bulan pertama Rp50.000,00, bulan kedua Rp55.000,00, bulan ketiga Rp60.000,00, dan seterusnya. Jumlah tabungan selama 10 bulan adalah . . . .
$A.\ Rp500.000,00$
$B.\ Rp550.000,00$
$C.\ Rp600.000,00$
$D.\ Rp700.000,00$
$E.\ Rp725.000,00$
Pembahasan soal UN UNBK matematika SMA IPS nomor 15.
Deret aritmetika:
$a = 50.000$
$b = 5.000$
$n = 10$
$S_n = \dfrac{n}{2}(2a + (n - 1)b)$
$S_n = \dfrac{10}{2}(2.(50.000) + (10 - 1)5.000)$
$S_n = 5(145.000)$
$S_n = 725.000,00$ → E.
$16.\displaystyle \lim_{x \to 3} \dfrac{x^2-x-6}{x^2-x-20} =$ . . . .
$A.\ -2$
$B.\ -1$
$C.\ 0$
$D.\ 1$
$E.\ ∞$
Pembahasan soal UN UNBK matematika SMA IPS nomor 16.
Karena bukan limit $\dfrac{0}{0}$, langsung substitusikan $x = 3$ ke dalam persamaan.
$\displaystyle \lim_{x \to 3}\dfrac{x^2-x-6}{x^2-x-20}$
$= \dfrac{3^2-3-6}{3^2-3-20}$
$= \dfrac{0}{-14}$
$= 0$
$17.\ \displaystyle \lim_{x \to 4}\dfrac{x^2-16}{x^2-x-12} =$ . . . .
$A.\ 4$
$B.\ 2$
$C.\ 1$
$D.\ \dfrac{5}{7}$
$E.\ \dfrac{8}{7}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 17.
Karena $\dfrac{0}{0}$, sederhanakan dengan memfaktorkan.
$\displaystyle \lim_{x \to 4}\dfrac{x^2-16}{x^2-x-12}$
$= \displaystyle \lim_{x \to 4}\dfrac{(x + 4)(x - 4)}{(x - 4)(x + 3)}$
$= \displaystyle \lim_{x \to 4}\dfrac{(x + 4)}{(x + 3)}$
$= \dfrac{(4 + 4)}{(4 + 3)}$
$= \dfrac{8}{7}$ → E.
Cara cepat:
Pakai aturan L'Hopital yaitu dengan menurunkan atas dan bawah.
$\displaystyle \dfrac{x^2-16}{x^2-x-12}$
$= \displaystyle \dfrac{2x}{2x - 1}$
$= \dfrac{2.4}{2.4 - 1}$
$= \dfrac{8}{7}$
$18$. Turunan pertama fungsi $f(x) = (5x - 3)^3$ adalah . . . .
$A.\ f'(x) = 3((5x - 3)^2$
$B.\ f'(x) = 5((5x - 3)^2$
$C.\ f'(x) = 8((5x - 3)^2$
$D.\ f'(x) = 15((5x - 3)^2$
$E.\ f'(x) = 45((5x - 3)^2$
Pembahasan soal UN UNBK matematika SMA IPS nomor 18.
Jika $f(x) = [g(x)]^n$ maka $f'(x) = n[g(x)]^{n-1}.g'(x)$
$f(x) = (5x - 3)^3$
$f'(x) = 3(5x - 3)^2.5$
$f'(x) = 15(5x - 3)^2$ → D.
$19$. Grafik fungsi $f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 6x + 2$ turun pada interval . . . .
$A.\ -2 < x < 3$
$B.\ -3 < x < 2$
$C.\ 2 < x < 3$
$D.\ x < -2\ atau\ x > 3$
$E.\ x < -3\ atau\ x > 2$
Pembahasan soal UN UNBK matematika SMA IPS nomor 19.
Fungsi naik jika $f'(x) > 0$
Fungsi turun jika $f'(x) < 0$
$f(x) = \dfrac{1}{3}x^3 - \dfrac{1}{2}x^2 - 6x + 2$
$f'(x) = x^2 - x - 6 < 0$
$(x + 2)(x - 3) < 0$
$-2 < x < 3$ → A.
$20.\ \displaystyle \int_{0}^{2}x(3x + 5)dx =$ . . . .
$A.\ 18$
$B.\ 16$
$C.\ 15$
$D.\ 10$
$E.\ 6$
Pembahasan soal UN UNBK matematika SMA IPS nomor 20.
Ingat !
$\displaystyle \int ax^ndx = \frac{a}{n + 1}x^{n + 1} + c$
$\displaystyle \int_{0}^{2}x(3x + 5)dx$
$= \displaystyle \int_{0}^{2}(3x^2 + 5x)dx$
$= (x^3 + \dfrac{5}{2}x^2)|_{0}^{2}$
$= 2^3 + \dfrac{5}{2}.2^2 - (0^3 + \dfrac{5}{2}.0^2)$
$= 8 + 10$
$= 18$ → A.
$21.\ \displaystyle \int_{-1}^{2}(6x^2 + 8x)dx =$ . . . .
$A.\ 24$
$B.\ 26$
$C.\ 28$
$D.\ 30$
$E.\ 32$
Pembahasan soal UN UNBK matematika SMA IPS nomor 21.
$\displaystyle \int_{-1}^{2}(6x^2 + 8x)dx = (2x^3 + 4x^2)|_{-1}^{2}$
$= (2.2^3 + 4.2^2 - (2.(-1)^3 + 4(-1)^2)$
$= 16 + 16 - (-2 + 4)$
$= 30$ → D.
$22$. Diketahui segitiga $ABC$ siku-siku di C dan $sin A = \dfrac{2}{7}$. Nilai $tan\ B$ adalah . . . .
$A.\ \dfrac{3}{5}\sqrt{5}$
$B.\ \dfrac{4}{5}\sqrt{5}$
$C.\ \dfrac{2}{3}\sqrt{5}$
$D.\ \dfrac{3}{5}\sqrt{5}$
$E.\ \dfrac{1}{3}\sqrt{5}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 22.
Perhatikan gambar diatas.
Jika $sin\ A = \dfrac{2}{7}$, maka sisi depan sudut $A = 2$ dan sisi miring $= 7$. Terlihat dengan jelas bahwa $tan\ B = \dfrac{3}{2}\sqrt{5}$ → A.
$23$. Nilai dari $cos 210^{\circ}.sin 330^{\circ} - cos 60^{\circ}$ adalah . . . .
$A.\ -\dfrac{1}{4}(2 - \sqrt{3})$
$B.\ -\dfrac{3}{4}(2 - \sqrt{3})$
$C.\ 0$
$D.\ \dfrac{1}{4}(2 - \sqrt{3})$
$E.\ \dfrac{3}{4}(2 - \sqrt{3})$
Pembahasan soal UN UNBK matematika SMA IPS nomor 23.
$cos 210^{\circ}.sin 330^{\circ} - cos 60^{\circ}$
$= cos (180 + 30)^{\circ}.sin (360 - 30)^{\circ} - cos 60^{\circ}$
$= -cos 30^{\circ}.(-sin 30^{\circ}) - cos 60^{\circ}$
$= -\dfrac{1}{2}\sqrt{3}.(-\dfrac{1}{2}) - \dfrac{1}{2}$
$= \dfrac{1}{4}\sqrt{3} - \dfrac{1}{2}$
$= \dfrac{1}{4}(\sqrt{3} - 2)$
$= -\dfrac{1}{4}(\sqrt{3} + 2)$ → A.
$24$. Sebuah tangga menyandar pada dinding dengan kemiringan $60^{\circ}$. Jika panjang tangga 5 meter, jarak dari kaki tangga ke dinding adalah . . . .
$A.\ \dfrac{5}{2}\ meter$
$B.\ \dfrac{5}{2}\sqrt{2}\ meter$
$C.\ \dfrac{5}{2}\sqrt{3}\ meter$
$D.\ 5\sqrt{2}\ meter$
$E.\ 5\sqrt{3}\ meter$
Pembahasan soal UN UNBK matematika SMA IPS nomor 24.
Perhatikan gambar dibawah!
$cos 60^{\circ} = \dfrac{x}{5}$
$\dfrac{1}{2} = \dfrac{x}{5}$
$x = \dfrac{5}{2}$ → A.
$25.\ \dfrac{sin\ x}{tan^2\ x} =$ . . . .
$A.\ sin\ x.tan\ x$
$B.\ sin\ x.cot\ x$
$C.\ cos\ x.tan\ x$
$D.\ cos\ x.cot\ x$
$E.\ sec\ x.tan\ x$
Pembahasan soal UN UNBK matematika SMA IPS nomor 25.
$\dfrac{sin\ x}{tan^2\ x} = \dfrac{sin\ x}{\dfrac{sin^2\ x}{cos^2\ x}}$
$= \dfrac{sin\ x.cos^2\ x}{sin^2\ x}$
$= \dfrac{cos^2\ x}{sin\ x}$
$= \dfrac{cos\ x}{sin\ x}.cos\ x$
$= cot\ x.cos\ x$ → D.
$26$. Besar sudut antara ruas garis AG dan bidang EFGH pada kubus ABCD.EFGH adalah $\alpha$. Nilai $cos \alpha$ adalah . . . .
$A.\ \dfrac{1}{3}\sqrt{3}$
$B.\ \dfrac{1}{2}\sqrt{3}$
$C.\ \dfrac{1}{3}\sqrt{6}$
$D.\ \dfrac{1}{2}\sqrt{6}$
$E.\ \dfrac{1}{3}\sqrt{3}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 26.
Perhatikan gambar di atas!
Panjang $AG = a\sqrt{3}$ → diagonal ruang.
Panjang $EG = a\sqrt{2}$ → diagonal sisi.
$cos\ \alpha = \dfrac{EG}{AG}$
$= \dfrac{a\sqrt{2}}{a\sqrt{3}}$
$= \dfrac{\sqrt{2}}{\sqrt{3}}$
$= \dfrac{1}{3}\sqrt{6}$ → C.
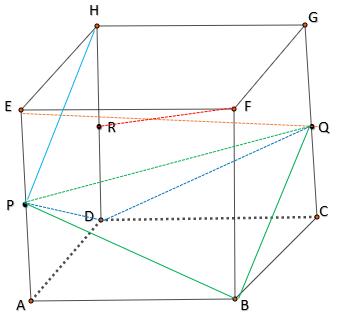
$27$. Berikut ini adalah pernyataan-pernyataan tentang kubus ABCD.EFGH dengan P, Q, R berturut-turut titik-titik tengah rusuk AE, CG, dan DH.
(1) Ruas garis QE dan RF berpotongan
(2) Ruas garis QB dan PB tegak lurus
(3) Ruas garis QB dan HP tidak sejajar
(4) Segitiga PDQ samakaki
Pernyataan yang benar adalah . . . .
A. (1) dan (2)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
E. (3) dan (4)
Pembahasan soal UN UNBK matematika SMA IPS nomor 27.
Perhatikan gambar di atas!
$\bullet$ Ruas garis QE dan RF pasti berpotongan.
$\bullet$ Ruas garis QB dan PB tidak tegak lurus.
Panjang PQ = AC = $a\sqrt{2}$. Karena segitiga
ABC siku-siku di B, tidak mungkin segitiga PBQ
siku-siku di B, karena PB tidak sama dengan AC.
$\bullet$ Ruas garis QB dan HP adalah sejajar.
$\bullet$ Segitiga PDQ sama kaki. Panjang DP sama dengan DQ.
Jadi jawab yang benar adalah (1) dan (4) → B.
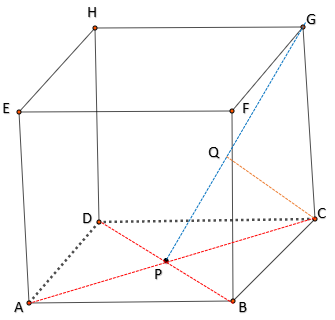
$28$. Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Titik P terletak di tengah diagonal sisi AC. Jarak dari titik C ke garis GP adalah . . . .
$A.\ 4\sqrt{3}$
$B.\ 4\sqrt{2}$
$C.\ 3\sqrt{3}$
$D.\ 3\sqrt{2}$
$E.\ 2\sqrt{3}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 28.
Perhatikan gambar di atas!
$AC = 6\sqrt{2}$ → $PC = \dfrac12AC = 3\sqrt{2}$
$PG^2 = PC^2 + CG^2$
$PG^2 = (3\sqrt{2})^2 + 6^2$
$PG^2 = 18 + 36$
$PG = 3\sqrt{6}$
$CQ = \dfrac{PC.CG}{PG}$
$CQ = \dfrac{3\sqrt{2}.6}{3\sqrt{6}}$
$CQ = 2\sqrt{3}$ → E.
Cara cepat:
Untuk soal yang sejenis, misalnya jarak antara titik A ke garis EP, jarak antara D ke garis HP, dan lain-lain, gunakan RUMUS $R = \dfrac{1}{3}a\sqrt{3}$
R → jarak, dan a panjang rusuk kubus.
Dari soal: $R = \dfrac{1}{3}.6.\sqrt{3} = 2\sqrt{3}$.
$29$. Data nilai ujian matematika di suatu kelas disajikan pada tabel distribusi frekwensi kumulatif "kurang dari". Banyak siswa yang memperoleh nilai 40 - 59 adalah . . . .
$A.\ 7$
$B.\ 8$
$C.\ 10$
$D.\ 18$
$E.\ 26$
Pembahasan soal UN UNBK matematika SMA IPS nomor 29.
Tabel distribusi frekwensinya adalah seperti di bawah.
Berarti banyak siswa yang memperoleh nilai
40 - 59 adalah 8 orang. → B.
$30$. Tabel berat badan sekelompok siswa.
Modus dari berat badan siswa adalah . . . .
$A.\ 49,06\ kg$
$B.\ 50,20\ kg$
$C.\ 50,40\ kg$
$D.\ 51,33\ kg$
$E.\ 51,83\ kg$
Pembahasan soal UN UNBK matematika SMA IPS nomor 30.
Kelas modus adalah $(49 - 54)$ → $M_1 = 49 - 0,5 = 48,5$
$d_1 = 14 - 10 = 4$
$d_2 = 14 - 8 = 6$
Panjang kelas $c = 36,5 - 30,5 = 6$
$M_o = M_1 + \dfrac{d_1}{d_1 + d_2}.c$
$M_o = 48,5 + \dfrac{4}{4 + 6}.6$
$M_o = 48,5 + \dfrac{4}{10}.6$
$M_o = 48,5 + 2,4$
$M_o = 50,9$ → Tidak ada jawaban.
$31$. Perhatikan berat badan dari kelompok siswa!
Kuartil bawah dari berat badan siswa adalah . . . .
$A.\ 37,00\ kg$
$B.\ 42,00\ kg$
$C.\ 45,50\ kg$
$D.\ 53,25\ kg$
$E.\ 53,78\ kg$
Pembahasan soal UN UNBK matematika SMA IPS nomor 31.
Kuartil bawah: $n = \sum f = 40$
$\dfrac{1}{4}n = \dfrac{1}{4}.40 = 10$
Berarti kuartil bawah terletak pada kelas (40 - 44)
$L_1 = 40 - 0,5 = 39,5$
$f^1 = 7$ → jumlah frekwensi yang ada di atas kelas
kuartil bawah. Dalam soal ini 3 + 4 = 7.
$f_1 = 6$ → Frekwensi kelas kuartil bawah.
Panjang kelas $c = 34,5 - 29,5 = 5$
$Q_1 = L_1 + \dfrac{\dfrac{1}{4}n - f^1}{f_1}.c$
$Q_1 = 39,5 + \dfrac{\dfrac{1}{4}.40 - 7}{6}.5$
$Q_1 = 39,5 + \dfrac{1}{2}.5$
$Q_1 = 39,5 + 2,5$
$Q_1 = 42,00$ → B.
$32$. Simpangan rata-rata dari data 6,5,7,5,6,8,7,6,6,7,4,5
adalah . . . .
$A.\ \dfrac{7}{3}$
$B.\ \dfrac{5}{3}$
$C.\ \dfrac{7}{5}$
$D.\ \dfrac{3}{5}$
$E.\ \dfrac{5}{6}$
Pembahasan soal UN UNBK matematika SMA IPS nomor 32.
$\overline{x} = \dfrac{4 + 3.5 + 4.6 + 3.7 + 8}{12}$
$\overline{x} = \dfrac{72}{12} = 6$
$SR = \dfrac{\displaystyle \sum_{i=1}^{n}|x_i - \overline{x}|}{n}$
$= \dfrac{|4 - 6| + 3.|5 - 6| + 4.|6 - 6| + 3.|6 - 7| + |8 - 6|}{12}$
$= \dfrac{2 + 3 + 0 + 3 + 2}{12}$
$= \dfrac{10}{12}$
$= \dfrac{5}{6}$
jawab: E.
$33$. Dari 8 orang calon termasuk Joko akan dipilih 4 orang sebagai pengurus kelas, yaitu sebagai ketua, wakil ketua, sekretaris, dan bendahara. Banyaknya susunan pengurus kelas yang mungkin terjadi, jika Joko harus menjadi ketua kelas adalah . . . .
$A.\ 35\ susunan$
$B.\ 56\ susunan$
$C.\ 210\ susunan$
$D.\ 336\ susunan$
$E.\ 1680\ susunan$
Pembahasan soal UN UNBK matematika SMA IPS nomor 33.
Karena Joko sudah dipastikan menduduki posisi ketua kelas, maka yang harus dipilih adalah posisi wakil ketua kelas, sekretaris, dan bendahara yang harus dipilih dari 7 orang sisa.
Banyak cara $=\ _{4}^{7}\textrm{P}$
$= \dfrac{7!}{(7-3)!}$
$= \dfrac{7!}{4!}$
$= \dfrac{7.6.5.4!}{4!}$
$= 7.6.5$
$= 210$ susunan → C.
$34$. Seorang ibu akan memilih 4 bunga dari 8 macam bunga. Banyak cara yang mungkin untuk memilih bunga tersebut adalah . . . .
$A.\ 24\ cara$
$B.\ 32\ cara$
$C.\ 70\ cara$
$D.\ 1.680\ cara$
$E.\ 40.320\ cara$
Pembahasan soal UN UNBK matematika SMA IPS nomor 34.
Banyak cara = $_{4}^{8}\textrm{C}$
$= \dfrac{8!}{(8-4)!.4!}$
$= \dfrac{8!}{4!.4!}$
$= \dfrac{8.7.6.5.4!}{4.3.2.1.4!}$
$= \dfrac{8.7.6.5}{4.3.2.1}$
$= 70$ cara → C.
$35$. Sebuah dadu dan sebuah koin dilambungkan satu kali secara bersama-sama. Peluang muncul gambar pada koin dan bilangan genap pada dadu adalah . . . .
$A.\ \dfrac14$
$B.\ \dfrac12$
$C.\ \dfrac23$
$D.\ \dfrac34$
$E.\ \dfrac67$
Pembahasan soal UN UNBK matematika SMA IPS nomor 35.
Perhatikan tabel di atas!
Banyak ruang sampel $n(S) = 12$
Gambar pada koin dan bilangan genap pada dadu ada 3 anggota → $n(A) = 3$
$P(A) = \dfrac{n(A)}{n(S)} = \dfrac{3}{12} = \dfrac{1}{4}$ → A.
$36$. Dari 7 kartu yang diberi huruf S, U, C, I, P, T, O diambil sebuah kartu secara acak. Jika pengambilan dilakukan sebanyak 70 kali dengan pengembalian, frekwensi harapan yang terambil huruf vokal adalah . . . .
$A.\ 20\ kali$
$B.\ 30\ kali$
$C.\ 40\ kali$
$D.\ 50\ kali$
$E.\ 60\ kali$
Pembahasan soal UN UNBK matematika SMA IPS nomor 36.
$n(S) = 7$
$n(A) = 3$
$P(A) = \dfrac{n(A)}{n(S)}$
$P(A) = \dfrac{3}{7}$
$F_h = P(A).BP$ → BP = Banyak Percobaan
$F_h = \dfrac{3}{7}.70$
$F_h = 30$ kali → B.
ISIAN
$37$. Pak Amir membeli 10 kg beras dan 5 kg gula dengan harga Rp185.000,00. Di toko yang sama Pak Budi membeli 15 kg beras dan 5 kg gula dengan harga Rp240.000,00. Harga 1 kg beras di toko tersebut adalah . . . . rupiah.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 37.
misalkan jumlah beras = x
misalkan jumlah gula = y
10x + 5y = 185.000 → 2x + y = 37.000 . . . . (1)
15x + 5y = 240.000 → 3x + y = 48.000 . . . . (2)
Eliminasi persamaan (1) dan (2)
2x + y = 37.000
3x + y = 48.000
----------------------------- $-$
x = 11.000
jadi harga 1 kg beras = Rp11.000,00. → 11.000
$38$. Setiap 3 tahun jumlah pengguna telepon genggam di kota Rayland bertambah 2 kali lipat jumlah semula. Jika pada tahun 2015 pengguna telepon genggam di sana adalah 28.800 orang, jumlah pengguna telepon genggam pada tahun 2006 di kota tersebut adalah . . . . orang.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 38.
Deret Geometri:
$r = 2$
$n = \dfrac{2015 - 2006}{3} + 1 = \dfrac{9}{3} + 1 = 4$
$U_n = 28.800$
$a =\ .\ .\ .\ .\ ?$
$U_n = ar^{n - 1}$
$28.800 = a.2^{4 - 1}$
$28.800 = 8a$
$a = \dfrac{28.800}{8}$
$a = 3.600$.
jadi banyak pengguna telepon genggam pada tahun
2006 adalah 3.600 orang. → 3.600
$39$. Biaya produksi setiap P barang adalah $(50P + P^2)$ ribu rupiah. Harga jual setiap unit barang tersebut adalah 100 ribu rupiah. Banyaknya unit yang dijual agar keuntungan maksimum adalah . . . . unit.
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 39.
Harga jual P unit = $100P$ (dalam ribu)
Biaya produksi P unit $= 50P + P^2$ (dalam ribu)
Misalkan keuntungan adalah K.
$K(P) = 100P - (50P + P^2)$
$K(P) = -P^2 + 50P$
$K'(P) = -2P + 50 = 0$
$2P = 50$
$P = 25$
Banyak unit yang dijual = 25 unit → 25
$40$. Dari angka 1,2,3,4,5,6 dan 8 akan dibentuk bilangan genap yang terdiri atas 3 angka berlainan. Banyaknya kemungkinan bilangan berbeda yang dapat dibentuk adalah . . . .
(Tuliskan jawaban dalam angka saja)
Pembahasan soal UN UNBK matematika SMA IPS nomor 40.
Banyaknya bilangan genap = $6.5.4 = 120$. → 120
www.maretong.com










Alhamdulillah, soal2 nya sangat bagus dan membantu persiapan UN
ReplyDeletelesprivat99.com