Daftar isi
Pengertian Lingkaran
Rumus dan Cara Menghitung Luas dan Keliling Lingkaran maupun Luas dan keliling daerah yang diarsir serta Contoh Soal dan Pembahasan lengkap. Lingkaran adalah kumpulan titik-titik yang memiliki jarak yang sama terhadap titik tertentu.Unsur-Unsur Lingkaran
Perhatikan unsur-unsur lingkatran pada gambar di atas!
AB → diameter lingkaran.
OA = OB = OC → jari-jari lingkaran.
Garis lengkung AB, AC, BC, AD, dan BD → busur lingkaran.
Garis AB, AC, dan AD → tali busur lingkaran.
Garis OE → apotema.
Daerah $p$ → juring lingkaran.
Daerah $q$ → tembereng.
Rumus Luas dan Keliling Lingkaran
Rumus Luas Lingkaran:
$L = \pi r^2$ atau $L = \dfrac14 \pi d^2$
$d = 2r\ atau\ r = \dfrac12d$
Rumus Keliling Lingkaran:
$K = 2 \pi r$ atau $K = \pi d$
Jika jari-jari lingkaran merupakan kelipatan 7, lebih baik menggunakan $\pi = \dfrac{22}{7}$.
Perlu diketahui bahwa persoalan tentang luas dan keliling lingkaran tidak selalu sederhana, karena kadang-kadang yang diketahui dari soal bukanlah jari-jari atau diameter lingkaran tetapi keliling, panjang busur, dan luas juring. Supaya lebih jelas, pelajari soal dan pembahasan luas dan keliling lingkaran berikut.
Contoh Soal dan Pembahasan Luas dan Keliling Lingkaran
Soal nomor 1:Diketahui jari-jari lingkaran 14 cm, maka luas lingkaran tersebut adalah . . . . $cm^2$
A. 154
B. 234
C. 436
D. 616
[Rumus dan Cara Menghitung Luas Lingkaran]
A. 154
B. 234
C. 436
D. 616
[Rumus dan Cara Menghitung Luas Lingkaran]
Pembahasan:
$\begin{align}
L &= \pi r^2\\
&= \pi.r.r\\
&= \dfrac{22}{7}.14.14\\
&= \dfrac{22}{\cancel7}.\cancelto2{14}.14\\
&= 22.2.14\\
&= 616\ cm^2\\
\end{align}$
jawab: D.
Soal nomor 2:
Diketahui lingkaran berdiameter 20 cm, maka luas lingkaran tersebut adalah . . . . $cm^2$.
A. 31,4
B. 62,8
C. 314
D. 628
[Rumus dan Cara Menghitung Luas Lingkaran]
A. 31,4
B. 62,8
C. 314
D. 628
[Rumus dan Cara Menghitung Luas Lingkaran]
Pembahasan:
$\begin{align}
L &= \dfrac14 \pi d^2\\
&= \dfrac{1}{4}.3,14.20^2\\
&= \dfrac{1}{\cancel4}.3,14.\cancelto{100}{400}\\
&= 3,14.100\\
&= 314\ cm^2\\
\end{align}$
jawab: B.
Soal nomor 3:
Keliling lingkaran berjari-jari 21 cm adalah . . . . cm.
A. 66
B. 108
C. 132
D. 154
[Rumus dan Cara Menghitung Keliling Lingkaran]
A. 66
B. 108
C. 132
D. 154
[Rumus dan Cara Menghitung Keliling Lingkaran]
Pembahasan:
$\begin{align}
K &= 2\pi r\\
&= 2. \dfrac{22}{\cancel7}.\cancelto3{21}\\
&= 2.22.3\\
&= 132\ cm^2\\
\end{align}$
jawab: C.
Soal nomor 4:
Keliling lingkaran berjari-jari 12 cm dalah . . . . cm.
A. 65,32
B. 75,36
C. 84,20
D. 88,24
[Rumus dan Cara Menghitung Keliling Lingkaran]
A. 65,32
B. 75,36
C. 84,20
D. 88,24
[Rumus dan Cara Menghitung Keliling Lingkaran]
Pembahasan:
$\begin{align}
K &= 2 \pi r\\
&= 2.3,14.12\\
&= 75,36\ cm\\
\end{align}$
jawab: B.
Soal nomor 5:
Diketahui lingkaran dengan diameter 10,5 cm, maka keliling lingkaran tersebut adalah . . . . cm.
A. 22
B. 33
C. 44
D. 66
[Rumus dan Cara menghitung Keliling Lingkaran]
A. 22
B. 33
C. 44
D. 66
[Rumus dan Cara menghitung Keliling Lingkaran]
Pembahasan:
$\begin{align}
K &= \pi d\\
&= \dfrac{22}{\cancelto2{7}}.\cancelto3{10,5}\\
&= \dfrac{\cancelto{11}{22}.3}{\cancel2}\\
&= 11.3\\
&= 33\ cm\\
\end{align}$
jawab: B.
Soal nomor 6:
Jika diketahui luas lingkaran adalah $38,5\ cm^2$, maka diameter lingkaran tersebut adalah . . . . cm.
A. 3,5
B. 7
C. 10,5
D. 14
[Rumus dan Cara Menghitung Luas Lingkaran]
A. 3,5
B. 7
C. 10,5
D. 14
[Rumus dan Cara Menghitung Luas Lingkaran]
Pembahasan:
$\begin{align}
L &= \dfrac14 \pi d^2\\
38,5 &= \dfrac14 \pi d^2 \text{→ semua dikali 4}\\
4.38,5 &= \pi d^2\\
154 &= \dfrac{22}{7}.d^2 \text{→ semua dikali 7}\\
7.154 &= 22.d^2 \text{→ semua dibagi 22}\\
\dfrac{7.\cancelto7{154}}{\cancel{22}} &= d^2\\
7.7 &= d^2\\
7 &= d\\
\end{align}$
jawab: B.
Soal nomor 7:
Diketahui dua lingkaran dengan jari-jari masing-masing 12 cm dan 16 cm. Perbandingan luas kedua lingkaran adalah . . . .
A. 5 : 6
B. 5 : 8
C. 7 : 12
D. 9 : 16
[Rumus dan Cara menghitung Perbandingan Luas Lingkaran]
A. 5 : 6
B. 5 : 8
C. 7 : 12
D. 9 : 16
[Rumus dan Cara menghitung Perbandingan Luas Lingkaran]
Pembahasan:
$\begin{align}
\dfrac{L_1}{L_2} &= \dfrac{\pi r_1^2}{\pi r_2^2}\\
&= \dfrac{\pi. r_1. r_1}{\pi.r_2.r_2}\\
&= \dfrac{\cancel{\pi}.\cancelto3{12}.\cancelto3{12}}{\cancel{\pi}.\cancelto4{16}.\cancelto4{16}}\\
&= \dfrac{3.3}{4.4}\\
&= \dfrac{9}{16}\\
L_1 : L_2 &= 9 : 16\\
\end{align}$
jawab: D.
Soal nomor 8:
Diketahui keliling suatu lingkaran adalah 125,6 cm. Luas lingkaran tersebut adalah . . . . $cm^2$.
A. 314
B. 628
C. 1256
D. 2512
[Rumus dan Cara Menghitung Luas Lingkaran]
A. 314
B. 628
C. 1256
D. 2512
[Rumus dan Cara Menghitung Luas Lingkaran]
Pembahasan:
$\begin{align}
K &= 2\pi r\\
125,6 &= 2.3,14.r\\
r &= \dfrac{\cancelto{40}{125,6}}{2.\cancel{3,14}}\\
&= \dfrac{\cancelto{20}{40}}{\cancel2}\\
&= 20\\
L &= \pi r^2\\
&= 3,14.20^2\\
&= 3,14.400\\
&= 1256\ cm^2\\
\end{align}$
jawab: C.
Soal nomor 9:
Dua buah lingkaran memiliki jari-jari masing-masing 15 cm dan 18 cm. Perbandingan keliling kedua lingkaran adalah . . . .
A. 3 : 5
B. 4 : 7
C. 5 : 6
D. 6 : 7
[Rumus dan Cara Menghitung Perbandingan Keliling Lingkaran]
A. 3 : 5
B. 4 : 7
C. 5 : 6
D. 6 : 7
[Rumus dan Cara Menghitung Perbandingan Keliling Lingkaran]
Pembahasan:
$\begin{align}
\dfrac{K_1}{K_2} &= \dfrac{\cancel{2\pi} r_1}{\cancel{2 \pi} r_2}\\
&= \dfrac{r_1}{r_2}\\
&= \dfrac{\cancelto5{15}}{\cancelto6{18}}\\
&= \dfrac56\\
K_1 : K_2 &= 5 : 6\\
\end{align}$
jawab: C.
Soal nomor 10:
Sebuah meja berbentuk lingkaran dengan jari-jari 62 cm akan dipasangi taplak. Jika ukuran taplak 8 cm lebih dari ukuran meja dan harga kain taplak adalah Rp200.000,00 tiap $m^2$, maka harga taplak untuk meja tersebut adalah . . . .
A. Rp254.000,00
B. Rp308.000,00
C. Rp356.000,00
D. Rp408.000,00
[Rumus dan Cara Menghitung Luas Lingkaran Soal Cerita]
A. Rp254.000,00
B. Rp308.000,00
C. Rp356.000,00
D. Rp408.000,00
[Rumus dan Cara Menghitung Luas Lingkaran Soal Cerita]
Pembahasan:
Ukuran taplak lebih 8 cm dari ukuran meja, dengan demikian jari-jari taplak adalah 62 + 8 = 70 cm = 0,7 m.
Luas taplak:
$\begin{align}
L &= \pi r^2\\
&= \pi . r . r\\
&= \dfrac{22}{\cancel7}.\cancelto{0,1}{0,7}.0,7\\
&= 22.0,1.0,7\\
&= 1,54\ m^2\\
\end{align}$
Harga taplak:
$\begin{align}
H &= (Luas\ taplak) \times (Harga\ per\ meter)\\
&= 1,54 \times 200.000\\
&= 308.000\\
\end{align}$
jawab: B.
Soal nomor 11:
Sebuah taman berbentuk lingkaran memiliki luas $346,5\ m^2$. Sekeliling taman akan ditanami pohon dengan jarak 3 m. Banyak pohon yang dibutuhkan adalah . . . .
A. 11 batang
B. 15 batang
C. 22 batang
D. 25 batang
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
A. 11 batang
B. 15 batang
C. 22 batang
D. 25 batang
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
Pembahasan:
$\begin{align}
L &= \dfrac14 \pi d^2\\
346,5 &= \dfrac14 \pi d^2\\
4.346,5 &= \pi d^2\\
1386 &= \dfrac{22}{7} d^2\\
d^2 &= 1386 : \dfrac{22}{7}\\
&= \cancelto{63}{1386} \times \dfrac{7}{\cancel{22}}\\
&= 63.7\\
&= 9.7.7\\
&= 3^2.7^2\\
d &= 3.7\\
&= 21\\
K &= \pi d\\
&= \dfrac{22}{\cancel7}.\cancelto3{21}\\
&= 66\ m\\
\end{align}$
$\begin{align}
Banyak\ Pohon &= \dfrac{K}{Jarak\ Pohon}\\
&= \dfrac{66}{3}\\
&= 22\\
\end{align}$
Soal nomor 12:
Sebuah sepeda memiliki dua buah roda berjari-jari 42 cm. Setelah roda berputar 150 kali pada lintasan lurus, maka jarak yang ditempuh sepeda adalah . . . .
A. 542 m
B. 486 m
C. 396 m
D. 324 m
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
A. 542 m
B. 486 m
C. 396 m
D. 324 m
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
Pembahasan:
Jika roda berputar satu kali, maka jarak yang ditempuh oleh roda sama dengan keliling roda. Dengan demikian, jika roda berputar sebanyak n kali maka jarak yang ditempuh oleh roda adalah n dikali keliling roda. Secara matematis dirumuskan dengan:
$S = n.K$
$S = n.2\pi r$
S → jarak yang ditempuh roda.
r → jari-jari roda.
Dari soal diketahui:
$r = 42\ cm$
$n = 150$
$\begin{align}
S &= n.2\pi r\\
&= 150.2.\dfrac{22}{\cancel7}.\cancelto6{42}\\
&= 150.2.22.6\\
&= 39.600\ cm\\
&= 396\ m
\end{align}$
jawab: C.
Soal nomor 13:
Sebuah lintasan lari berbentuk lingkaran dengan jari-jari 63 meter. Untuk menempuh jarak 2.574 meter, seorang pelari harus melakukan putaran sebanyak . . . .
A. 4 putaran
B. 5,5 putaran
C. 6,5 putaran
C. 7 putaran
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
A. 4 putaran
B. 5,5 putaran
C. 6,5 putaran
C. 7 putaran
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
Pembahasan:
$r = 63\ m$
$S = 2574\ m$
$\begin{align}
S &= n.2\pi r\\
2574 &= n.2.\dfrac{22}{\cancel7}.\cancelto9{63}\\
2574 &= n.2.22.9\\
n &= \dfrac{\cancelto{117}{2574}}{2.\cancel{22}.9}\\
&= \dfrac{117}{18}\\
&= 6,5\ putaran
\end{align}$
jawab: C.
Soal nomor 14:
Diketahui jarak kota A dan kota B adalah 23,55 km. Untuk menempuh perjalanan dari kota A menuju kota B, roda sebuah sepeda harus berputar sebanyak 7.500 kali, maka jari-jari roda sepeda adalah . . . . $\pi = 3,14$
A. 42 cm
B. 50 cm
C. 56 cm
D. 60 cm
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
A. 42 cm
B. 50 cm
C. 56 cm
D. 60 cm
[Rumus dan Cara Menghitung Keliling Lingkaran Soal Cerita]
Pembahasan:
$\begin{align}
S &= 23,55\ km\\
&= 23.550\ m\\
&= 2.355.000\ cm\\
n &= 7.500\ kali\\
\end{align}$
$\begin{align}
S &= n.2\pi r\\
2355000 &= 7500.2.3,14.r\\
r &= \dfrac{\cancelto{314}{2355000}}{\cancel{7500}.2.3,14}\\
&= \dfrac{\cancelto{100}{314}}{2.\cancel{3,14}}\\
&= \dfrac{100}{2}\\
&= 50\ cm\\
\end{align}$
jawab: B.
Cara Menghitung Luas dan Keliling Daerah Lingkaran yang Diarsir
Soal nomor 15:Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Derah p, q, r, dan s masing-masing adalah setengah lingkaran dengan diameter 14 cm. Luas daerah p = luas daerah q = luas daerah r = luas daerah s. Dengan memperhatikan gambar, luas daerah yang diarsir (LA) adalah luas persegi ABCD $-$ luas daerah r $-$ luas daerah s + luas daerah p + luas daerah q. Karena luas daerah p = luas darah q = luas daerah r = luas daerah s, maka daerah yang diarsir (LA) = luas persegi ABCD.
$\begin{align}
LA &= AB . BC\\
&= 14 . 14\\
&= 196\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah garis warna merah. Panjang busur AB = panjang busur BC = panjang busur CD = panjang busur AD = keliling setengah lingkaran berdiameter 14 cm. Dengan memperhatikan gambar, keliling daerah yang diarsir (KA) = 2 kali keliling lingkaran berdiameter 14 cm.
$\begin{align}
KA &= 2 . \pi d\\
&= 2 . \dfrac{22}{\cancel7} . \cancelto2{14}\\
&= 2 . 22 . 2\\
&= 88\ cm\
\end{align}$
Soal nomor 16:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
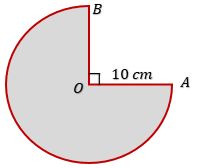
Luas daerah yang diarsir (LA) adalah luas dari $\dfrac34$ lingkaran berjari-jari 10 cm.
$\begin{align}
LA &= \dfrac34 . \pi r^2\\
&= \dfrac34 . 3,14 . 10^2\\
&= \dfrac34 . 3,14 . 100\\
&= 235,5\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah garis berwarna merah. Berdasarkan gambar, keliling daerah yang diarsir adalah keliling dari $\dfrac34$ lingkaran berjari-jari 10 cm + 2 kali jari-jari.
$\begin{align}
KA &= \dfrac34 . 2\pi r + OA + OB\\
&= \dfrac34 . 2 . 3,14 . 10 + 10 + 10\\
&= 47,1 + 10 + 10\\
& = 67,1\ cm\\
\end{align}$
Soal nomor 17:
Diketahui ABCD adalah sebuah persegi dengan panjang sisi 14 cm. Hitunglah luas dan keliling daerah yang diarsir pada gambar!
Pembahasan:
Perhatikan gambar dibawah!
Luas daerah yang diarsir (LA):
Luas daerah p adalah luas juring BAC dikurangi luas segitiga ABC. Luas juring BAC sama dengan luas seperempat lingkaran berjari-jari 14 cm. Luas daerah yang diarsir adalah dua kali luas daerah p.
$\begin{align}
Luas\ p &= \dfrac14 . \pi r^2 - \dfrac12 . AB . BC\\
&= \dfrac14 . \dfrac{22}{7} . r . r - \dfrac12 . AB . BC\\
&= \dfrac14 . \dfrac{22}{\cancel7} . \cancelto2{14} . 14 - \dfrac{1}{\cancel2} . \cancelto7{14} . 14\\
&= \dfrac{1}{\cancel4}. \cancelto{11}{44} . 14 - 7 . 14\\
&= 11. 14 - 7 . 14\\
&= (11 - 7). 14\\
&= 4 . 14\\
&= 56 \ cm^2\\
LA &= 2 . (luas\ p)\\
&= 2 . 56\\
&= 112\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Panjang busur AC = keliling seperempat lingkaran berjari-jari 14 cm. Keliling daerah yang diarsir adalah 2 kali panjang busur AC.
$\begin{align}
KA &= \cancel2. \dfrac{1}{\cancel4}. \cancel2\pi r\\
&= \pi r\\
&= \dfrac{22}{\cancel7}. \cancelto2{14}\\
&= 44\ cm\\
\end{align}$
Soal nomor 18:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p = luas daerah q = luas seperempat lingkaran berjari-jari 7 cm. Luas daerah p + luas daerah q = luas setengah lingkaran berjari-jari 7 cm. Luas daerah yang diarsir merupakan luas seperempat lingkaran berjari-jari 14 cm $-$ (luas daerah p + luas daerah q) $-$ luas persegi ABFE.
$\begin{align}
LA &= \dfrac14. \dfrac{22}{\cancel7}. \cancelto2{14}. 14 - \dfrac12. \dfrac{22}{\cancel7}. \cancel7. 7 - 7. 7\\
&= \dfrac{1}{\cancel4}. \cancelto{11}{44}. 14 - \dfrac{1}{\cancel2}. \cancelto{11}{22}. 7 - 7. 7\\
&= 11. 14 - 11. 7 - 7. 7\\
&= 22. 7 - 11. 7 - 7. 7\\
&= (22 - 11 - 7). 7\\
&= 4 . 7\\
&= 28\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah panjang busur CD + panjang busur CF + panjang busur DF. Panjang busur CD adalah keliling seperempat lingkaran berjari-jari 14 cm. Panjang busur CF = panjang busur DF = keliling seperempat lingkaran berjari-jari 7 cm. Panjang busur CF + Panjang busur DF = keliling setengah lingkaran berjari-jari 7 cm.
$\begin{align}
KA &= \dfrac14. 2 . \dfrac{22}{\cancel7} . \cancelto2{14} + \dfrac{1}{\cancel2}. \cancel2 . \dfrac{22}{\cancel7}. \cancel7\\
&= \dfrac{1}{\cancel4}. \cancelto{22}{88} + 22\\
&= 22 + 22\\
&= 44\ cm\\
\end{align}$
Soal nomor 19:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p = luas darah q = luas setengah lingkaran berdiameter 10,5 cm. Luas daerah p + luas daerah q = luas satu lingkaran berdiameter 10,5 cm. Luas daerah yang diarsir adalah luas setengah lingkaran berdiameter 21 cm $-$ (luas daerah p + luas daerah q).
$\begin{align}
LA &= \dfrac12. \dfrac14. \dfrac{22}{\cancel7}. \cancelto3{21}. 21 - \dfrac14. \dfrac{22}{\cancelto2{7}}.\cancelto3{10,5}. 10,5\\
&= \dfrac18. 22. 3. 21 - \dfrac18. 22. 3. 10,5\\
&= \dfrac18. 22. 3. 21 - \dfrac18. 11. 3. 21\\
&= \dfrac18. (22 - 11). 3. 21\\
&= \dfrac18. 11. 3. 21\\
&= \dfrac18. 693\\
&= 86,625\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah garis berwarna merah. Panjang busur OA = panjang busur OB = keliling setengah lingkaran berdiameter 10,5 cm. Panjang busur AB = keliling setengah lingkaran berdiameter 21 cm. Keliling daerah yang diarsir = panjang busur AB + panjang busur OA + panjang busur OB. Keliling daerah yang diarsir = keliling setengah lingkaran berdiameter 21 cm + keliling satu lingkaran berdiameter 10,5 cm.
$\begin{align}
\widehat{AB} &= \dfrac12 \pi d\\
&= \dfrac{1}{\cancel2}.\dfrac{\cancelto{11}{22}}{\cancel7}.\cancelto3{21}\\
&= 11.3\\
&= 33\ cm
\end{align}$
$\begin{align}
\widehat{OA} &= \dfrac12 \pi d\\
&= \dfrac{1}{\cancel2}.\dfrac{\cancelto{11}{22}}{\cancelto27}.\cancelto3{10,5}\\
&= 11.\dfrac32\\
&= 16,5\ cm\\
\widehat{OB} &= \widehat{OA}\\
&= 16,5\ cm\\
\end{align}$
$\begin{align}
KA &= \widehat{AB} + \widehat{OA} + \widehat{OB}\\
&= 33 + 16,5 + 16,5\\
&= 66\ cm\\
\end{align}$
Soal nomor 20:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p = luas daerah q = luas setengah lingkaran berdiameter 14 cm. Luas daerah yang diarsir adalah luas setengah lingkaran berdiameter 28 cm + luas daerah p $-$ luas daerah q. Karena luas daerah p = luas daerah q, maka luas daerah yang diarsir menjadi luas setengah lingkaran berdiameter 28 cm.
$\begin{align}
LA &= \dfrac12.\dfrac14\pi d^2\\
&= \dfrac18.\pi.d.d\\
&= \dfrac18.\dfrac{22}{\cancel7}.\cancelto4{28}.28\\
&= \dfrac{1}{\cancel8}.11.\cancel{2.4}.28\\
&= 11.28\\
&= 308\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah garis warna merah. Dengan memperhatikan gambar, keliling daerah yang diarsir adalah keliling setengah lingkaran berdiameter 28 cm + 2 kali keliling setengah lingkaran berdiameter 14 cm.
$\begin{align}
KA &= \dfrac{1}{\cancel2}.\dfrac{22}{\cancel7}.\cancelto2{28} + \bcancel2.\dfrac{1}{\bcancel2}.\dfrac{22}{\cancel7}.\cancelto2{14}\\
&= 22.2 + 22.2\\
&= 44 + 44\\
&= 88\ cm.
\end{align}$
Soal nomor 21:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Daerah r adalah setengah lingkaran berdiameter 14 cm, daerah p dan q masing-masing adalah seperempat lingkaran berjari-jari 7 cm. Perhatikan bahwa Luas daerah r = luas daerah p + luas daerah q. Luas daerah yang diarsir adalah luas daerah r + luas persegi panjang ABFG $-$ (luas daerah p + luas daerah q).
$L_r = L_p + L_q$
$\begin{align}
LA &= L_r + L_{ABFG} - (L_p + L_q)\\
&= L_{ABFG}\\
&= AB.BF\\
&= 14.7\\
&= 98\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Panjang busur FG = keliling setengah lingkaran berdiameter 14 cm. Panjang busur EG = panjang busur EF = keliling seperempat lingkaran berjari-jari 7 cm. Keliling daerah yang diarsir = Panjang busur FG + Panjang busur EG + panjang busur EF = keliling satu lingkaran berdiameter 14 cm.
$\begin{align}
KA &= \pi d\\
&= \dfrac{22}{\cancel7}.\cancelto2{14}\\
&= 22.2\\
&= 44\ cm\\
\end{align}$
Soal nomor 22:
Diketahui AB, AC, dan BC adalah diameter lingkaran. Hitunglah luas dan keliling daerah yang diarsir pada gambar berikut!
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir:
Luas daerah yang diarsir adalah luas setengah lingkaran berdiameter AC + luas setengah lingkaran berdiameter AB $-$ Luas setengah lingkaran berdiameter BC + luas segitiga ABC.
$\begin{align}
LA &= \dfrac18.\pi.24^2 + \dfrac18.\pi.7^2 - \dfrac18.\pi.25^2 + \dfrac{1}{\cancel2}.7.\cancelto{12}{24}\\
&= \dfrac18.\pi.(24^2 + 7^2 - 25^2) + 7.12\\
&= 0 + 84\\
&= 84\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah panjang busur AC + panjang busur AB + panjang busur BC.
$\begin{align}
KA &= \widehat{AC} + \widehat{AB} + \widehat{BC}\\
&= \dfrac12.\pi.24 + \dfrac12.\pi.7 + \dfrac12.\pi.25\\
&= \dfrac12.\pi.(24 + 7 + 25)\\
&= \dfrac{1}{\cancel2}.\pi.\cancelto{28}{56}\\
&= \pi.28\\
&= \dfrac{22}{\cancel7}.\cancelto4{28}\\
&= 22.4\\
&= 88\ cm\\
\end{align}$
Soal nomor 23:
Pembahasan:
Luas daerah yang diarsir (LA):
Dengan memperhatikan sudut juring, maka juring OAB dan juring OCD adalah seperlima lingkaran. Luas daerah yang diarsir adalah luas seperlima lingkaran dengan jari-jari 21 cm dikurangi luas seperlima lingkaran dengan jari-jari 14 cm.
$\begin{align}
LA &= \dfrac15.\pi.21.21 - \dfrac15.\pi.14.14\\
&= \dfrac15.\dfrac{22}{\cancel7}.\cancelto3{21}.21 - \dfrac15.\dfrac{22}{\cancel7}.\cancelto2{14}.14\\
&= \dfrac15.22.3.21 - \dfrac15.22.2.14\\
&= \dfrac15.22.(3.21 - 2.14)\\
&= \dfrac15.22(63 - 28)\\
&= \dfrac{1}{\cancel5}.22.\cancelto7{35}\\
&= 22.7\\
&= 154\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Panjang busur AB adalah seperlima keliling lingkaran berjari-jari 21 cm, panjang busur CD adalah seperlima keliling lingkaran berjari-jari 14 cm. Keliling daerah yang diarsir adalah panjang busur CD + panjang busur AB + panjang BC + panjang AD.
$\begin{align}
KA &= \dfrac15.2.\pi.21 + \dfrac15.2.\pi.14 + 7 + 7\\
&= \dfrac25.\dfrac{22}{\cancel7}.\cancelto3{21} + \dfrac25.\dfrac{22}{\cancel7}.\cancelto2{14} + 14\\
&= \dfrac25.22.3 + \dfrac25.22.2 + 14\\
&= \dfrac25.(22.3 + 22.2) + 14\\
&= \dfrac25.(66 + 44) + 14\\
&= \dfrac{2}{\cancel5}.\cancelto{22}{110} + 14\\
&= 2.22 + 14\\
&= 44 + 14\\
&= 58\ cm\\
\end{align}$
Soal nomor 24:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p + luas daerah q adalah luas satu lingkaran berdiameter 14 cm. Luas daerah yang diarsir adalah luas persegi panjang ABCD $-$ (luas daerah p + luas daerah q).
$\begin{align}
LA &= AB.BC - \dfrac14.\pi.d.d\\
&= 20.14 - \dfrac14.\dfrac{22}{\cancel7}.\cancelto2{14}.14\\
&= 20.14 - \dfrac{1}{\cancel4}.11.\cancel{2.2}.14\\
&= 20.14 - 11.14\\
&= (20 - 11).14\\
&= 9.14\\
&= 126\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Panjang AB = panjang CD = 20 cm. Panjang busur AD = panjang busur BC = keliling setengah lingkaran berdiameter 14 cm. Panjang busur AD + panjang busur BC = keliling satu lingkaran berdiameter 14 cm. Keliling daerah yang diarsir adalah garis berwarna merah = 2 kali panjang AB + keliling satu lingkaran berdiameter 14 cm.
$\begin{align}
KA &= 2.AB + \pi d\\
&= 2.20 + \dfrac{22}{\cancel7}.\cancelto2{14}\\
&= 2.20 + 22.2\\
&= 40 + 44\\
&= 84\ cm\\
\end{align}$
Soal nomor 25:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daera p = luas daerah q = luas seperempat lingkaran berjari-jari 14 cm. Dengan demikian luas daerah p + luas daerah q = luas setengah lingkaran berjari-jari 14 cm. Luas daerah r = luas daerah s = luas seperempat lingkaran berjari-jari 7 cm. Dengan demikian, luas daerah r + luas daerah s = luas setengah lingkaran berjari-jari 7 cm. Luas daerah yang diarsir adalah luas persegi ABCD $-$ (luas daerah p + luas daerah q) $-$ (luas daerah r + luas daerah s).
$\begin{align}
LA &= AB.BC - \dfrac12.\pi.14.14 - \dfrac12.\pi.7.7\\
&= 21.21 - \dfrac{1}{\cancel2}.\dfrac{22}{\cancel7}.\cancel{14}.14 - \dfrac{1}{\cancel2}.\dfrac{\cancelto{11}{22}}{\cancel7}.\cancel7.7\\
&= 21.21 - 22.14 - 11.7\\
&= 21.3.7 - 22.2.7 - 11.7\\
&= (21.3 - 22.2 - 11).7\\
&= (63 - 44 - 11).7\\
&= 8.7\\
&= 56\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah garis berwarna merah = keliling setengah lingkaran berjari-jari 14 cm + keliling setengah lingkaran berjari-jari 7 cm.
$\begin{align}
KA &= \dfrac12.2.\pi.14 + \dfrac12.2.\pi.7\\
&= \pi.14 + \pi.7\\
&= \dfrac{22}{\cancel7} .\cancelto2{14} + \dfrac{22}{\cancel7}.\cancel7\\
&= 22.2 + 22.1\\
&= 44 + 22\\
&= 66\ cm\\
\end{align}$
Soal nomor 26:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p + luas daerah q + luas daerah r = luas satu lingkaran berdiameter 21 cm. Luas daerah yang diarsir adalah luas daerah p + luas daerah q + luas daerah r = luas satu lingkaran berdiameter 21 cm.
$\begin{align}
LA &= \dfrac14\pi d^2\\
&= \dfrac{1}{4}.\pi.d.d\\
&= \dfrac{1}{4}.\dfrac{22}{\cancel7}.\cancelto3{21}.21\\
&= \dfrac{\cancelto{11}{22}.3.21}{\cancelto2{4}}\\
&= \dfrac{11.3.21}{2}\\
&= 346,5\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Keliling daerah yang diarsir adalah panjang busur AB + panjang busur OC + panjang busur OD + panjang garis AC + panjang garis BD. Panjang busur AB + panjang busur OC + panjang busur OD = keliling satu lingkaran berdiameter 21 cm. Panjang garis AC + panjang garis BD = panjang garis AB = 21 cm. Dengan demikian keliling daerah yang diarsir menjadi:
$\begin{align}
KA &= \pi d + d\\
&= \dfrac{22}{\cancel7}.\cancelto3{21} + 21\\
&= 22.3 + 21\\
&= 66 + 21\\
&= 87\ cm\\
\end{align}$
Soal nomor 27:
Pembahasan:
Perhatikan gambar di bawah!
Luas daerah yang diarsir (LA):
Luas daerah p + luas daerah q + luas daerah r + luas daerah s = luas satu lingkaran berjari-jari 7 cm. Luas daerah yang diarsir adalah luas persegi ABCD $-$ (luas daerah p + luas daerah q + luas daerah r + luas daerah s). Dengan demikian, luas daerah yang diarsir adalah luas persegi ABCD $-$ luas satu lingkaran berjari-jari 7 cm.
$\begin{align}
LA &= AB.BC - \pi r^2\\
&= AB.BC - \pi.r.r\\
&= 14.14 - \dfrac{22}{\cancel7}.\cancel7.7\\
&= 14.14 - 22.7\\
&= 14.14 - 11.2.7\\
&= 14.14 - 11.14\\
&= (14 - 11).14\\
&= 3.14\\
&= 42\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
Panjang busur EF + panjang busur FG + panjang busur GH + panjang busur EH = keliling satu lingkaran berjari-jari 7 cm. Keliling daerah yang diarsir adalah panjang busur EF + panjang busur FG + panjang busur GH + panjang busur EH = keliling satu lingkaran berjari-jari 7 cm.
$\begin{align}
KA &= 2\pi r\\
&= 2.\dfrac{22}{\cancel7}.\cancel7\\
&= 2.22\\
&= 44\ cm\\
\end{align}$
Soal nomor 28:
Pembahasan:
Luas daerah yang diarsir (LA):
Luas daerah yang diarsir adalah luas segitiga ABC dikurangi luas juring ABD.
$\begin{align}
LA &= \dfrac12.AB.AC - \dfrac{\cancel{60^o}}{\cancelto6{360^o}}.\pi.r.r\\
&= \dfrac{1}{\cancel2}.7.\cancelto{12}{24} - \dfrac{1}{\cancelto3{6}}.\dfrac{\cancelto{11}{22}}{\cancel7}.\cancel7.7\\
&= 7.12 - \dfrac{11.7}{3}\\
&= 84 - \dfrac{77}{3}\\
&= 84 - 25\dfrac23\\
&= 58\dfrac13\ cm^2\\
\end{align}$
Keliling daerah yang diarsir (KA):
$\begin{align}
BC^2 &= AB^2 + AC^2\\
&= 7^2 + 24^2\\
&= 49 + 576\\
&= 625\\
BC &= \sqrt{625}\\
&= 25\ cm\\
\\
BD &= AB = 7\ cm\\
CD &= BC - BD\\
&= 25 - 7\\
&= 18\\
\\
\widehat{AD} &= \dfrac{\cancel{60^o}}{\cancelto6{360^o}}.2.\dfrac{22}{\cancel7}.\cancel7\\
&= \dfrac{1}{\cancelto3{6}}.\cancel2.22\\
&= \dfrac{22}{3}\\
&= 7\dfrac13\\
\\
KA &= AC + \widehat{AD} + CD\\
&= 24 + 7\dfrac13 + 18\\
&= 49\dfrac13\ cm\\
\end{align}$
Soal nomor 29:
Sebuah stadion berbentuk lingkaran dengan diameter 84 meter. Sepanjang stadion akan dipasang lampu dengan jarak 4 meter. Hitunglah banyak lampu yang diperlukan!
Pembahasan:
$\begin{align}
K &= \pi d\\
&= \dfrac{22}{\cancel7}.\cancelto{12}{84}\\
&= 22.12\\
\end{align}$
$\begin{align}
Banyak\ Lampu &= \dfrac{K}{Jarak\ Lampu}\\
&= \dfrac{22.\cancelto3{12}}{\cancel4}\\
&= 22.3\\
&= 66\ lampu\\
\end{align}$
Soal nomor 30:
Gambar di bawah merupakan lintasan atletik dengan jari-jari lingkaran dalamnya 100 m dan jari-jari lingkaran luarnya 120 m.
a. Hitunglah luas daerah yang diarsir!
b. Jika biaya untuk membuat lintasan atletik Rp250.000,00 tiap meter kuadrat, hitunglah biaya total untuk membuat lintasan!
a. Hitunglah luas daerah yang diarsir!
b. Jika biaya untuk membuat lintasan atletik Rp250.000,00 tiap meter kuadrat, hitunglah biaya total untuk membuat lintasan!
Pembahasan:
a. Luas daerah yang diarsir adalah luas lingkaran berjari-jari 120 m $-$ luas lingkaran berjari-jari 100 m.
$\begin{align}
LA &= 3,14.120^2 - 3,14.100^2\\
&= 3,14.14400 - 3,14.10000\\
&= 314.144 - 314.100\\
&= 314.(144 - 100)\\
&= 314.44\\
&= 13816\ m^2
\end{align}$
b. Biaya total:
$\begin{align}
Biaya &= LA \times Harga\ Satuan\\
&= 13816 \times 250000\\
&= 3454000000\\
\end{align}$
Jadi biaya total = Rp3.454.000.000,00.
Demikianlah ulasan tentang luas dan keliling lingkaran, semoga bermanfaat.
BACA JUGA:
1. Sudut Pusat dan Sudut Keliling Lingkaran
2. Panjang Busur dan Luas Juring Lingkaran
3. Garis Singgung Persekutuan Dalam Dua Lingkaran
4. Garis Singgung Persekutuan Luar Dua Lingkaran
www.maretong.com






























Post a Comment for "Cara Menghitung Luas dan Keliling Lingkaran"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.