Daftar isi
Pengertian Garis Singgung Persekutuan Luar (GSPL) Dua Lingkaran
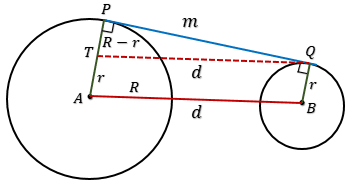
Rumus dan Cara Menghitung Garis Singgung Persekutuan Luar (GSPL) dua lingkaran serta Contoh Soal dan Pembahasan Lengkap. Perhatikan gambar di bawah!Diketahui lingkaran besar A dengan panjang jari-jari R dan lingkaran kecil B dengan panjang jari-jari r. Garis PQ merupakan garis singgung persekutuan luar lingkaran A dan lingkaran B dengan panjang PQ = m, sehingga garis AP dan garis BQ tegak lurus terhadap garis PQ (garis singgung lingkaran selalu tegak lurus dengan jari-jari lingkaran di titik singgung). Garis AB adalah garis yang menghubungkan titik pusat lingkaran A dengan titik pusat lingkaran B, sehingga AB = d merupakan jarak pusat kedua lingkaran. Garis QT sejajar dan sama panjang denga garis AB, sehingga AB = QT = d. Garis BQ sejajar dan sama panjang dengan garis AT, sehingga AT = BQ = r sehingga PT = R - r.
Rumus Garis Singgung Persekutuan Luar (GSPL) Dua Lingkaran
Perhatikan gambar lingkaran di atas!Segitiga PQT merupakan segitiga siku-siku yang siku-siku di titik P, dan QT merupakan sisi miring sehingga berlaku rumus Pythagoras:
$QT^2 = PQ^2 + PT^2$
Karena QT = AB = d, PQ = m, dan PT = R - r, maka:
$AB^2 = PQ^2 + (R - r)^2$
$PQ^2 = AB^2 - (R - r)^2$
$m^2 = d^2 - (R - r)^2$
$m = \sqrt{d^2 - (R - r)^2}$
m = PQ adalah panjang garis singgung persekutuan luar.
d = AB adalah jarak titik pusat kedua lingkaran.
R adalah panjang jari-jari lingkaran besar.
r adalah panjang jari-jari lingkaran kecil.
R > r.
Perlu diingat, bahwa PQ = m, (R - r), dan AB = d merupakan sisi-sisi sebuah segitiga siku-siku dimana AB merupakan sisi miring dan PQ dan (R - r) merupakan sisi siku-siku. Untuk lebih memahami tentang materi garis singgung persekutuan luar dua lingkaran, silahkan pelajari contoh soal yang berikut.
Contoh Soal dan Pembahasan Garis Singgung Persekutuan Luar Dua Lingkaran
Contoh Soal nomor 1:Diketahui dua lingkaran dengan pusat P dan Q, jarak PQ = 26 cm, panjang jari-jari lingkaran masing-masing 12 cm dan 2 cm. Panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah . . . .
A. 16 cm
B. 24 cm
C. 28 cm
D. 30 cm
[Garis Singgung Persekutuan Luar GSPL]
Pembahasan:
Perhatikan gambar di bawah!
d = PQ = 26 cm → Jarak kedua pusat lingkaran.
R = 12 cm → Jari-jari lingkaran besar.
r = 2 cm → Jari-jari lingkaran kecil.
$\begin{align}
m^2 &= d^2 - (R - r)^2\\
&= 26^2 - (12 - 2)^2\\
&= 26^2 - 10^2\\
&= 676 - 100\\
&= 576\\
m &= \sqrt{576}\\
&= 24\ cm\\
\end{align}$
jawab: B.
Cara cepat:
Seperti telah dibicarakan di atas bahwa d, m, dan (R - r) merupakan panjang sisi-sisi dari sebuah segitiga siku-siku. Dari soal diketahui d = 26 cm dan (R - r) = 10 cm, dengan demikian m = 24 cm. Ingat, angka 10, 24, dan 26 merupakan tripel Pythagoras.
Contoh Soal nomor 2:
Diketahui dua lingkaran berjari-jari masing-masing 12 cm dan 5 cm. Jika panjang garis singgung persekutuan luarnya 24 cm, maka jarak titik pusat kedua lingkaran tersebut adalah . . . .
A. 36 cm
B. 30 cm
C. 25 cm
D. 17 cm
[Garis Singgung Persekutuan Luar (GSPL)]
Pembahasan:
R = 12 cm → Jari-jari lingkaran besar.
r = 5 cm → Jari-jari lingkaran kecil.
m = 24 cm → Panjang garis singgung persekutuan luar.
$m^2 = d^2 - (R - r)^2$
$\begin{align}
d^2 &= m^2 + (R - r)^2\\
&= 24^2 + (12 - 5)^2\\
&= 24^2 + 7^2\\
&= 576 + 49\\
&= 625\\
d &= \sqrt{625}\\
&= 25\ cm\\
\end{align}$
jawab: C.
Cara cepat:
Karena m, (R - r), dan d merupakan panjang sisi-sisi sebuah segitiga siku-siku, dengan pemahaman tentang tripel Pythagoras kita bisa melihat apakah panjang sisi-sisi segitiga merupakan tripel Pythagoras atau tidak. Diketahui m = 24, (R - r) = 7, dengan demikian d = 25. Ingat, angka 7, 24, dan 25 merupakan tripel Pythagoras.
Contoh Soal nomor 3.
Panjang garis singgung persekutuan luar dua buah lingkaran yang berpusat di P dan Q 24 cm. Jika panjang jari-jari lingkaran kecil 4 cm dan jarak titik pusat kedua lingkaran 25 cm, maka panjang jari-jari lingkaran lainnya adalah . . . .
A. 7 cm
B. 10 cm
C. 11 cm
D. 12 cm
[Garis Singgung Persekutuan Luar (GSPL)]
Pembahasan:
m = 24 cm
r = 4 cm
d = 25 cm
$m^2 = d^2 - (R - r)^2$
$\begin{align}
(R - r)^2 &= d^2 - m^2\\
(R - 4)^2 &= 25^2 - 24^2\\
&= 625 - 576\\
&= 49\\
(R - 4) &= \sqrt{49}\\
R - 4 &= 7\\
R &= 7 + 4\\
&= 11\ cm\\
\end{align}$
jawab: C.
Cara cepat:
d = 25 cm, m = 24 cm, dengan demikian (R - r) = 7 cm. Hal ini terjadi karena 7, 24, dan 25 merupakan tripel Pythagoras.
R - r = 7
R - 4 = 7
R = 7 + 4
R = 11 cm.
Contoh Soal nomor 4:
Jari-jari lingkaran yang berpusat di A sama dengan 2 kali jari-jari lingkaran yang berpusat di B. Jika panjang garis singgung persekutuan luar kedua lingkaran itu 36 cm dan jarak kedua pusatnya 39 cm, maka panjang jari-jari lingkaran A adalah . . . .
A. 15 cm
B. 20 cm
C. 25 cm
D. 30 cm
[Garis Singgung Persekutuan Luar (GSPL)]
Pembahasan:
R = 2r → Jari-jari lingkaran besar sama dengan dua kali jari-jari lingkaran kecil.
m = 36 → Panjang garis singgung persekutuan luar.
d = 39 cm → Jarak pusat kedua lingkaran.
$m^2 = d^2 - (R - r)^2$
$\begin{align}
(R - r)^2 &= d^2 - m^2\\
(2r - r)^2 &= 39^2 - 36^2\\
r^2 &= 1521 - 1296\\
&= 225\\
r &= \sqrt{225}\\
&= 15\\
R &= 2r\\
&= 2.15\\
&= 30\ cm\\
\end{align}$
jawab: D.
Contoh Soal nomor 5:
Perhatikan gambar di bawah!
Jika luas daerah yang diarsir adalah $165\ cm^2$, maka panjang AB adalah . . . .
A. 15 cm
B. 17 cm
C. 20 cm
D. 25 cm
[Garis Singgung Persekutuan Luar (GSPL)]
Pembahasan:
R = 15 cm → Jari-jari lingkaran besar.
r = 7 cm → Jari-jari lingkaran kecil.
$\begin{align}
Luas\ ABPQ &= \dfrac{AP + BQ}{2} \times PQ\\
165 &= \dfrac{15 + 7}{2} \times PQ\\
165 &= \dfrac{22}{2} \times PQ\\
165 &= 11PQ\\
PQ &= 15\\
\end{align}$
m = PQ = 15 cm.
$\begin{align}
d^2 &= m^2 + (R - r)^2\\
&= 15^2 + (15 - 7)^2\\
&= 15^2 + 8^2\\
&= 225 + 64\\
&= 289\\
d &= \sqrt{289}\\
&= 17\ cm
\end{align}$
jawab: B.
Contoh Soal nomor 6:
Perhatikan gambar di bawah!
Tiga buah pipa paralon dengan penampang berbentuk lingkaran berjari-jari 14 cm diikat seperti gambar. Panjang tali terpendek yang dapat digunakan untuk mengikat ketiga pipa paralon tersebut adalah . . . .
A. 148 cm
B. 160 cm
C. 172 cm
D. 186 cm
[Garis singgung Persekutuan Luar (GSPL)]
Pembahasan:
Perhatikan gambar!
Keliling lingkaran berjari-jari r = 14 cm:
$\begin{align}
K &= 2 \pi\ r\\
&= 2 \times \dfrac{22}{7} \times 14\\
&= 88\ cm\\
\end{align}$
Perhatikan segitiga berwarna merah! Segitiga berwarna merah merupakan segitiga sama sisi, sehingga sudut-sudut dalam segitiga tersebut adalah $60^o$. Keliling segitiga warna merah (KSWM) dapat dihitung dengan rumus:
$\begin{align}
KSWM &= 2r + 2r + 2r\\
& = 6r\\
&= 6.14\\
&= 84\ cm\\
\end{align}$
Panjang busur BC, DE, dan FA:
$\begin{align}
\widehat{BC} &= \dfrac{120^o}{360^o} \times K\\
&= \dfrac13K\\
\end{align}$
$\widehat{BC} = \widehat{DE} = \widehat{FA} = \dfrac13K$
$\begin{align}
\widehat{BC} + \widehat{DE} + \widehat{FA} &= \dfrac13K + \dfrac13K + \dfrac13K\\
&= K\\
&= 88\ cm\\
\end{align}$
Panjang tali minimum (PTM):
$\begin{align}
PTM &= KSWM + \widehat{BC} + \widehat{DE} + \widehat{FA}\\
&= 84 + 88\\
&= 172\ cm\\
\end{align}$
jawab: C.
Cara cepat:
Untuk susunan pipa seperti gambar, panjang tali minimum (PTM) dapat dihitung dengan rumus:
$\begin{align}
PTM &= 2nr + 2 \pi r\\
&= 2.3.14 + 2.\dfrac{22}{7}.14\\
&= 84 + 88\\
&= 172\ cm\\
\end{align}$
n → banyak pipa.
r → jari-jari pipa.
Contoh Soal nomor 7:
Perhatikan dambar di bawah!
Enam pipa paralon dengan penampang seperti gambar berjari-jari 21 cm saling bersinggungan luar. Panjang tali minimum yang dapat digunakan untuk mengikat keenam pipa paralon tersebut adalah . . . .
A. 284 cm
B. 312 cm
C. 384 cm
D. 406 cm
[Garis Singgung Persekutuan Luar (GSPL)]
Pembahasan:
Perhatikan gambar!
Keliling lingkaran berjari-jari r = 21 cm:
$\begin{align}
K &= 2 \pi r\\
&= 2 \times \dfrac{22}{7} \times 21\\
&= 132\ cm\\
\end{align}$
Panjang busur BC, DE, FG, HA:
$\begin{align}
\widehat{BC} &= \dfrac{90^o}{360^o} \times K\\
&= \dfrac14K
\end{align}$
$\begin{align}
\widehat{DE} = \widehat{FG} = \widehat{HA} = \widehat{BC} &= \dfrac14K\\
\widehat{BC} + \widehat{DE} + \widehat{FG} + \widehat{HA} &= \dfrac14K + \dfrac14K + \dfrac14K + \dfrac14K\\
&= K\\
&= 132\ cm\\
\end{align}$
Keliling persegi panjang warna merah:
$\begin{align}
KPWM &= 4r + 2r + 4r + 2r\\
&= 12r\\
&= 12.21\\
&= 252\ cm\\
\end{align}$
Panjang tali minimum (PTM):
$\begin{align}
PTM &= KPWM + \widehat{BC} + \widehat{DE} + \widehat{FG} + \widehat{HA}\\
&= 252 + 132\\
&= 384\ cm\\
\end{align}$
jawab: C.
Cara cepat:
Untuk susunan pipa seperti gambar, panjang tali minimum (PTM) dapat dicari dengan rumus:
$\begin{align}
PTM &= 2nr + 2 \pi r\\
&= 2.6.21 + 2.\dfrac{22}{7}.21\\
&= 252 + 132\\
&= 384\ cm\\
\end{align}$
n → banyak pipa.
r = jari-jari pipa.
Demikianlah ulasan tentang garis singgung persekutuan luar dua lingkaran, semoga bermanfaat.
BACA JUGA:
Teorema dan Tripel Pythagoras
www.maretong.com






Post a Comment for "Garis Singgung Persekutuan Luar (GSPL)"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.